Шаблон:Test transclude/npc infobox below/old/test
Тривиальный узел (или незаузлённый узел, англ. unknot) — геометрический узел, объемлюще-изотопный стандартному вложению окружности в трёхмерную сферу, а также объемлюще-изотопический класс такого геометрического узла. Под окружностью здесь подразумевается подмножество евклидовой плоскости, а под стандартным вложением окружности в трёхмерную сферу – вложение , где или любое аналогичное отображение, отправляющее плоскость в одну из координатных плоскостей трёхмерного пространства.[1] Эквивалентно можно определить тривиальный узел как геометрический узел, который продолжается до гладкого вложения двумерного диска в трёхмерную сферу, а также объемлюще-изотопический класс такого геометрического узла. Иными словами, любой геометрический узел, для которого существует гладко вложенный в трёхмерную сферу двумерный диск, границей которого является этот геометрический узел, называется тривиальным узлом и все тривиальные узлы являются объемлюще-изотопными.[2] Узел, не являющийся тривиальным, принято называть нетривиальным узлом.[3] Тривиальный узел играет существенную роль в различных задачах теории узлов и обладает рядом уникальных свойств. СвойстваправитьКомбинаторные свойстваправить
Доказательство Пусть – геометрический узел, причем . Если узел допускает диаграмму без перекрёстков, то, по определению, существует такая гиперплоскость в , проекция множества на которую является простой замкнутой кривой, лежащей в этой гиперплоскости. Зафиксируем и обозначим через произвольное вложение окружности в трёхмерную сферу, такое что совпадает с этой кривой, лежащей в гиперплоскости. Кривая , как кривая в , объемлюще-изотопна простой замкнутой кривой по построению. Не умаляя общности можно считать, что упомянутая выше гиперплоскость является, например, координатной -плоскостью в . Известно[5], что любые две простые замкнутые кривые в плоскости объемлюще-изотопны друг другу как кривые в плоскости, то есть кривая объемлюще-изотопна стандартному вложению окружности в -плоскость. Объемлющую изотопию -плоскости можно продолжить до изотопии всей трёхмерной сферы тождественно по третьей координате, а потому кривая и стандартное вложение окружности в трёхмерную сферу объемлюще-изотопны как кривые в . Тогда по транзитивности геометрический узел объемлюще-изотопен стандартному вложению окружности в трёхмерную сферу, а значит тривиален. Алгебраические свойстваправить
Простота тривиального узлаправить
Эквивалентная переформулировка теоремы о простоте тривиального узла вносит ясность в устройство моноида узлов, а именно, утверждает, что ни один нетривиальный элемент этого моноида не имеет обратного. Этот элементарный, но нетривиальный результат имеет несколько независимых доказательств. Топологические свойстваправить
Геометрические свойстваправить
Алгоритмическое распознавание тривиального узлаправить Классический вопрос алгоритмической теории узлов — задача распознавания тривиального узла. Задача состоит в том, чтобы создать алгоритм, который по поданной на вход диаграмме узла выводил бы ответ, является ли данный узел тривиальным. Существует ряд алгоритмов, решающих эту задачу, однако основной вопрос на данный момент остаётся открытым, а именно, существует ли полиномиальный алгоритм распознавания тривиального узла. Стоит отметить, что диаграммы тривиального узла могут быть очень сложными как к визуальному, так и к машинному распознаванию. Классическим примером «трудной» диаграммы тривиального узла является так называемый «Гордиев узел Хакена». Числа развязыванияправитьС тривиальным узлом связан ряд инвариантов, обобщённо называемых числа развязывания. Исторически первым подобным инвариантом было классическое число развязывания узла, то есть минимальное количество применений преобразования переключения перекрёстков, необходимое для превращения данного узла в тривиальный. Несколько позже, с развитием теории преобразований узлов, появились соответствующие инварианты и для других преобразований, например, число H(2)-развязываний или число Δ-развязываний.[7][8] Примечанияправить
Литератураправить
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Трилистник (или узел-трилистник, англ. trefoil knot) — общее название для двух простейших нетривиальных узлов. Левый и правый трилистники – единственные узлы, допускающие диаграмму с тремя перекрёстками, при том, что любая диаграмма с меньшим числом перекрёстков представляет тривиальный узел[1]. Стоит отметить, что в научной литературе по теории узлов нередко можно встретить словосочетание «узел трилистник», которое от случая к случаю может подразумевать и один конкретный трилистник из двух существующих, и пару из двух трилистников с намёком на то, что утверждение, использующее этот термин, справедливо для них обоих, и использование такого определения самого узла, в котором между левым и правым трилистниками в принципе нет никакого различия (существование не обязательно сохраняющего ориентацию гомеоморфизма пар вместо существования объемлющей изотопии в качестве отношения эквивалентности геометрических узлов)[2]. Более подробно этот терминологический вопрос обсуждается в разделе «Определение». Левый и правый трилистники являются зеркальными образами друг друга, а потому обладают очень сходными наборами присущих им свойств. Однако всё же некоторые тонкие инварианты, такие как многочлен HOMFLY-PT или сигнатура[англ.], способны установить их формальное различие. Ещё одним дополнительным обстоятельством, способствующим существованию единого названия «трилистник» для обоих узлов, является то, что большинство классический табуляций в связи с экономией места не различают зеркальные узлы друг от друга. Будучи простейшими узлами сразу по ряду показателей, трилистники нередко выступают как классические примеры или контр-примеры в различных теоретико-узловых рассуждениях, наряду с другим «несложным» узлом восьмёркой[3]. Выдвигаемые гипотезы или обширные концепции нередко в первую очередь оказываются проверены и изучены именно в случае трилистников, если это представляется возможным в рамках предположений[4]. Во многом в связи с этим трилистники – одни из наиболее подробно исследованных узлов. Трилистники часто возникают в химии и молекулярной биологии как форма заузленности молекул (в таких случаях они иногда называются молекулярными или органическими трилистниками), являясь в этом виде классическими представителями пересечения абстрактной топологии с естественными науками[5][6]. Кроме того, различные изображения трилистников встречаются на многих артефактах разных культур и эпох – трилистники нередко использовались в качестве мистического или религиозного символа (в этом смысле чаще встречаются более локальные и специальные понятия вроде трикветр или валькнут), а также в искусстве, например, как составная часть росписей, узоров или мозаик. В современном мире символ трилистника не менее популярен и различные стилизованные изображения трилистников нередко можно встретить на эмблемах и логотипах, в качестве декоративных элементов или в произведениях искусства. Наряду с кольцами Борромео, зацеплением Хопфа, тривиальным узлом и некоторыми другими понятиями как классической теории узлов, так и топологии в целом, трилистники являются ключевым объектом в изложении и практике спорного[7] психоаналитического исследования философов Жака Лакана и Жана-Мишеля Вапперо[8]. Определениеправить
Когда речь заходит о трилистниках, в математической литературе обычно даётся одновременно некорректное и остенсивное определение, а именно, приводится изображение одного (правого или левого) трилистника и подпись вида «на этом рисунке изображён узел трилистник»[9][10][2][11][12]. Чаще всего это связано с предполагаемым уровнем знаний читателя – в работах для начинающих излагаемые ниже тонкие детали предполагаются несущественными, а в изданиях для профессионалов – хорошо известными. Кроме того, существует и другая неоднозначность – на рисунке справа (как и везде далее) трилистники называются левым и правым в соответствии с обозначениями книги Кунио Мурасуги «Knot Theory & Its Applications» (Murasugi, 1996), однако в этом случае нет общего устоявшегося соглашения о нотации. Так, например, в другом классическом учебнике «Knot theory» Чарльза Ливингстона (Livingston, 1996) используются противоположные обозначения[13][14][15]. Конечно, в случае определения с помощью рисунка, всегда подразумевается, что соответствующим трилистником называется любой геометрический узел, объемлюще-изотопный геометрическому узлу, образ которого изображён на рисунке, а также соответствующий объемлюще-изотопический класс. Нередко слова «левый» и «правый» в принципе оказываются опущены в изложении. В таком случае обычно один из двух трилистников называется «трилистником», а другой — его «зеркальным образом». Действительно, левый и правый трилистники являются зеркальными образами друг друга, то есть диаграмма, полученная одновременным переключением всех перекрёстков на произвольной диаграмме правого трилистника, оказывается диаграммой левого трилистника и наоборот (определение зеркального образа корректно, так как «зеркальные отражения» движений Рейдемейстера являются движениями Рейдемейстера). Кроме того, нетривиальным результатом является и то, что подобная терминология в принципе осмыслена, а левый и правый трилистники — действительно различные нетривиальные узлы, то есть являются несовпадающими объемлюще-изотопическими классами геометрических узлов. Впервые этот результат получил[16] Макс Ден в 1914 году, исследуя введенную им в этой же работе группу узла вместе с так называемой «периферической системой» в виде меридиана и параллели, однако со временем появились и другие, менее трудоёмкие способы различить два трилистника, к примеру раскраски узлов или полиномиальные инварианты[17]. Хотя визуальное определение и является наиболее распространённым, существует ряд и более аккуратных эквивалентных определений, пусть и задействующих некоторые дополнительные концепции. Косыправить
Правым трилистником называется любой геометрический узел, объемлюще изотопный замыканию Александера косы с двумя нитями, а также соответствующий объемлюще-изотопический класс. Торические узлыправить
Правым трилистником называется торический узел . Иными словами, правым трилистником называется любой геометрический узел, объемлюще изотопный простой замкнутой кривой в , заданной параметрически как и лежащей на торе а также соответствующий объемлюще-изотопический класс. Рациональные тэнглыправитьПравым трилистником называется любой геометрический узел, объемлюще изотопный числителю рационального тэнгла с дробью , а также соответствующий объемлюще-изотопический класс. В каждом из приведённых выше случаев левый трилистник можно определить либо по аналогии, заменяя соответствующие знаки на противоположные, либо как зеркальный образ правого трилистника по определению. Кроме того, заметим, что иногда термин «трилистник» всё таки имеет место быть без дополнительных уточнений. Дело в том, что всё изложенное выше (и далее) подразумевает работу с определением узла, основанном на понятии объемлющей изотопии. Существует также и эквивалентное этому определение, где под узлом также понимается некоторый класс эквивалентности геометрических узлов, но два геометрических узла теперь называются эквивалентными, если существует соответствующий гомеоморфизм пар (образ узла, трёхмерная сфера), переводящий образ одного геометрического узла в образ другого и сохраняющий ориентацию трёхмерной сферы[2]. Однако в некоторых работах условие сохранения ориентации опускается, в связи с чем, оказывается допустимым гомеоморфизм, реализующий зеркальное отражение. Иными словами, в определении, не учитывающем сохранение ориентации, узел и его зеркальный образ являются одним и тем же узлом по определению. В частности, в таком определении левый и правый трилистники ничем не различаются и корректно использование одного слова для указания на любой из них. Но в связи с тем, что такое определение хоть и удобно для пользования в свете определенных задач и вопросов, но утрачивает достаточно широкий круг деталей, всё изложение настоящей статьи производится в объемлюще-изотопическом смысле. СвойстваправитьКомбинаторныеправить



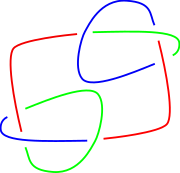
Топологическиеправить
Геометрическиеправить
Алгебраическиеправить
СимметрииправитьОба трилистника являются двусторонними узлами, иначе говоря:
Кроме того, оба трилистника являются периодическими с периодом [35]. Трилистники в других областях знанийправитьМолекулярная биологияправить С восьмидесятых годов двадцатого века в молекулярной биологии активно исследуются механически соединённые молекулярные структуры, аналогичные обыкновенным макроскопическим узлам – молекулярные узлы. Трилистники, как наиболее геометрически простые узлы, нередко оказываются выделены как непосредственно природно, так и в процессе исследований. Так, например, трилистники являются самой распространённой формой заузливания белков в естественной природе[36], а первым искусственно синтезированным молекулярным узлом был левый трилистник, полученный Жан-Пьером Соважем и коллегами в 1989 году[37]. Зоологияправить Глубоководные бесчелюстные существа миксины обладают способностью завязывать собственное длинное и гибкое тело в узел трилистник (чаще всего левый), причем эта способность носит вполне утилитарный характер. Так, например, если миксине грозит опасность, она завязывает собственный хвост узлом, выделяет ядовитый слизистый секрет и начинает продвигать узел далее по телу, нанося секрет по всей его длине и обволакивая себя ядовитым коконом из слизи. Позже аналогичным образом миксина очищает себя от слизистого покрытия, сдвигая узел из собственного тела в обратную сторону[1]. Психоанализ Лаканаправить В психоаналитической теории Лакана идея «узла-трилистника» играет ключевую роль в описании структуры паранойи. Впервые Лакан упоминает узел трилистник (здесь и далее без уточнения о том, правый или левый), на семинаре RSI (22 семинар) в 1974 году, где сообщает, что этот узел тесно связан с зацеплением Борромео – трилистник получается из зацепления Борромео путем переклеивания нитей в трёх перекрёстках – между Воображаемым и Реальным, между Символическим и Воображаемым и между Реальным и Символическим. Лакан подчеркивает, что после этого преобразования утрачивается наличие трёх компонент, «регистры больше не могут быть дифференцированы», но «форма» зацепления Борромео остаётся, и всё ещё можно определить «местоположение четырёх отверстий, в которых находятся различные типы наслаждения». Такое преобразование он называет «непрерывностью» или «интерференцией между регистрами». Связь трилистника с паранойей объясняется уже в 23 семинаре в 1975 году: «если субъект связывает в тройку воображаемое, символическое и реальное, то он поддерживается только своей непрерывностью, эти три составляют одну и ту же последовательность. И это то, из чего состоит паранойяльный психоз»[38]. Эту идею развивает Жан-Мишель Вапперо в своей работе «Узел», где говорит об узле трилистнике как о паранойяльном бреде[39]. Не смотря на широкую популярность и культовый статус теоретико-узлового метода Лакана среди его учеников и последователей, научная общественность скептически относится к подобного рода исследованиям, ставя под сомнение не только уместность пространных аналогий между топологическими объектами и психическими состояниями, но и в принципе осмысленность тех или иных терминов, предложений или даже текстов Лакана. Так, например, Жан Брикмон и Алан Сокал в своей работе «Интеллектуальные уловки: критика современной философии постмодерна» резюмируют математическую составляющую работ Лакана следующим образом: «…его аналогии между психоанализом и математикой невообразимо произвольны, и он не даёт им абсолютно никакого концептуального или эмпирического оправдания. В конечном счёте, мы думаем, что вышеприведённые тексты служат красноречивым свидетельством выставленной напоказ поверхностной эрудиции и манипулирования фразами, лишёнными смысла...»[7]. Символические изображения трилистниковправитьИскусство, религия и культураправить
Геральдика и Вексиллологияправить
Нумизматикаправить
Эмблемы и логотипыправить
Примечанияправить
ЛитератураправитьМатематические материалы
Прочее
Ссылкиправить
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В теории узлов узел «Лапчатка», известный также как печать Соломона или пятилистник, — это один из двух узлов с числом пересечений пять, другой узел — трижды скрученный узел. Узел перечислен как узел 51 в записи Александера-Бриггса[англ.] и может быть также описан как (5,2)-торический узел. Лапчатка является замкнутой версией двойного узла[англ.].  Лапчатка является простым узлом, его число закрученности равно 5 и он является обратимым, но он не амфихирален[1]. Его многочлен Александера равен
многочлен Конвея равен
а его многочлен Джонса равен
Удивительно, но это те же самые полиномы Александера, Конвея и Джонса, что и у узла 10132[3]. Однако многочлен Кауфмана может быть использован для различения этих двух узлов. Название «лапчатка» узел получил по аналогии с пятилепестковым цветком лапчатка. См. такжеправитьПримечанияправить
Литератураправить
Документация
Шаблон автоматически включает статьи в категорию в категорию «Незавершённые статьи по математике».
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Обозначение= L2a1 Число нитей = 2 Длина косы= 2 Число пересечений= 2 Коэффициент зацепления= 1 Гиперболический объём= 0 Класс= тор Зацепление Хопфа — простейшее нетривиальное зацепление с двумя и более компонентами[1], состоит из двух окружностей, зацеплённых однократно[2] и названо по имени Хайнца Хопфа[3]. Геометрическое представлениеправитьКонкретная модель состоит из двух единичных окружностей в перпендикулярных плоскостях, таких что каждая проходит через центр другой[2]. Эта модель минимизирует длину верёвки[англ.] (длина верёвки — инвариант теории узлов) зацепления и до 2002 года зацепление Хопфа являлось единственным, у которого длина верёвки была известна [4]. Выпуклая оболочка этих двух окружностей образует тело, называемое олоидом[5]. СвойстваправитьВ зависимости от относительной ориентации[англ.] двух компонент коэффициент зацепления Хопфа равен ±1[6]. Зацепления Хопфа является (2,2)-торическим зацеплением[7] с описывающим словом[8] . Дополнение зацепления Хопфа — , цилиндр над тором[9]. Это пространство имеет локально евклидову геометрию, так что зацепление Хопфа не является гиперболическим. Группа узлов зацепления Хопфа (фундаментальная группа его дополнения) — это (свободная абелева группа на двух генераторах) и она отличает зацепление Хопфа от двух незацеплённых окружностей, которым соответствует свободная группа на двух генераторах[10]. Зацепление Хопфа не может быть раскрашено в три цвета. Это непосредственно следует из факта, что зацепление можно раскрасить лишь в два цвета, что противоречит второй части определения раскраски. В каждом пересечении будет максимум 2 цвета, так что при раскраске мы нарушим требование иметь 1 или 3 цвета в каждом пересечении, либо нарушим требование иметь более 1 цвета. Расслоение ХопфаправитьРасслоение Хопфа — это непрерывное отображение из 3-сферы (трёхмерная поверхность в четырёхмерном евклидовом пространстве) в более привычную 2-сферу, такое, что прообраз каждой точки на 2-сфере является окружностью. Таким образом получается разложение 3-сферы на непрерывное семейство окружностей и каждые две различных окружности из этого семейства образуют зацепление Хопфа. Этот факт и побудил Хопфа заняться изучением зацеплений Хопфа — поскольку любые два слоя зацеплены, расслоение Хопфа является нетривиальным расслоением[англ.]. С этого началось изучение гомотопических групп сфер[11]. Историяправить Зацепление названо именем тополога Хайнца Хопфа, исследовавшего его в 1931 году в работе по расслоению Хопфа[12]. Однако такое зацепление использовал ещё Гаусс[3], а вне математики оно встречалось задолго до этого, например, в качестве герба японской буддийской секты Бузан-ха[англ.], основанной в XVI столетии. См. такжеправить
Примечанияправить
Литератураправить
Ссылкиправить
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
    У́зел Соломо́на (лат. sigillum Salomonis) — общее название для традиционного декоративного украшения, используемого с древних времён и найденного во многих культурах. Вопреки названию, это, с точки зрения теории узлов, зацепление, а не узел. СтруктураправитьУзел Соломона состоит из двух замкнутых петель, которые дважды переплетены. Другими словами, в плоском виде узел Соломона имеет четыре скрещивания, в которых две петли чередующимся образом проходят под (или над) друг другом (в отличие от двух скрещиваний, в более простом зацеплении Хопфа). В большинстве художественных изображений части петель, которые проходят снизу (или сверху) друг от друга, образуют центральный квадрат, а продолжения петель выступают в четырёх направлениях. Эти выступы могут быть овальными, квадратными, треугольными, или могут завершаться фигурами произвольной формы, такими как листья, мечи, крылья. РаспространениеправитьУзел Соломона часто встречается в мозаиках Древнего Рима, обычно в виде двух переплетённых овалов. В национальном парке Сепфориса (Израиль) узел Соломона выложен в виде каменной мозаики на древней синагоге. В отделе археологии Национального музея Ирландии в Дублине выставлен Крест Конга[англ.], относящийся к XII веку. В отличие от тщательной отделки всего креста, на нём видны два очень маленьких узла Соломона в простой форме, расположенных по обеим сторонам кварцевого кристалла. По преданию, в центре этого креста под кварцевым кристаллом находится пустота, в которой когда-то находилась щепка от «Животворящего Креста», на котором, по преданию был распят Иисус Христос. На Ближнем Востоке узел Соломона является исламской традицией. Он появляется над дверным проходом в начале XII века в мечетях и медресе в Каире. Два варианта узла Соломона найдены на недавно раскопанной мозаике в Ятте. К востоку узел был воткан в древний среднеазиатский молитвенный коврик. К западу узел Соломона появляется в Мусульманской Испании, и он сияет в стеклянном окне конца двадцатого столетия мечети в США. В Британском музее в Лондонв есть египетский коран XIV века с узлом Соломона на обложке. Музей Фаулера Культурной Истории Университета Калифорнии в Лос-Анджелесе содержит большую африканскую коллекцию, включающую стеклянные бусы XIX века народа йоруба и маски, украшенные узлами Соломона. Здание Мавзолея Мира (еврейское кладбище, Лос-Анджелес) содержит изображения узла Соломона на каменных и бетонных барельефах, созданных в 1934 году. В Греческом Православном Соборе Святой Софии («Византийский район» Лос-Анджелеса) имеется икона из оливкового дерева (Epitaphios — похороны Христа) с узлами Соломона, вырезанными в каждом углу. В университетской библиотеке Пауэла (Лос-Анджелес) потолочные балки в главном читальном зале покрыты узлами Соломона. Построенный в 1926 читальный зал также имеет Купол Мудрости, по краям которого расположены узлы Соломона. В орнаменте южносахалинской Сибири и у курильских айнов[1]. В вышивке Тверской, Владимирской, Тамбовской, Воронежской губерний встречается мотив в виде двух скрещенных овалов, обнаружен он и на орнаментированных предметах из славянских курганов XII—XIII веков, на металлическом чекане из Биляра, датируемом началом II тысячелетия и. э. Примечательно, что мотив этот имеется и в чувашской вышивке[2] и аналогичен булгарским перстням.[источник не указан 1253 дня]. В монографическом исследовании узоров народной вышивки Г. С. Масловой свастика считается свойственной крестьянской культуре всего Русского Севера.[3] В яргических знаках кельтских узоров[4]. На браслете в санкт петербургских курганах, как элемент восточной орнаментации (узел счастья), проникший из Золотой Орды[5]. Во второй половине XIX в. появляются труды А. И. Махно и М. Квитко, где приводятся изображения четырёхногой ярги на образцах ткачества и вышивки южнорусских крестьянок[6]. В работах о женской одежде Поднепровья культуры средневековья восточных славян и новгородских крестах[7]. Является символом «kramo bone» в адинкре.  Встречается на деревянных предметах в Новгороде[8] . НазваниеправитьНа латинском языке конфигурация известна под названием sigillum Salomonis, что буквально означает «печать Соломона». Название ассоциируется с библейским правителем Соломоном, известным своим умом и знаниями (а по некоторым легендам и магической силой). На английский, да и на русский, название обычно переводится как «узел Соломона», поскольку «печать царя Соломона» имеет другие значения (либо Звезда Давида, либо гексаграмма). При изучении древних мозаик узел Соломона часто упоминается как «гильош» или «двойной узел», а узел Соломона в центре декоративного узора из четырёх закруглённых дуг известен как «свастика пельта» (pelta — латинское название щита). Среди других названий, употребляемых сейчас: «Основной узел» (Foundation Knot) относится к плетению и является основой многих кельтских мотивов и используется в США при вязании и плетении макраме. «Имболо» (Imbolo) относится к узлу на тканях народа Куба в Конго.[9] Символизмправить   Узел использовался во многих культурах и исторических эрах и ему можно дать ряд интерпретаций. Поскольку нет видимого начала и конца, он может представлять бессмертие и вечность — как это делает более сложный буддистский бесконечный узел. Поскольку узел выглядит как сплетение двух фигур, его иногда интерпретируют как Узел Влюблённых, хотя это имя также употребляется для другого узла[англ.]. Ввиду связи с религией узел иногда понимается как символ веры, но, в то же время, он появляется во многих местах как мирской символ авторитета, важности, красоты. Узел Соломона появляется на могильных камнях и мавзолеев еврейских кладбищ и в катакомбах многих наций. В этом контексте узел Соломона интерпретируется как символ вечности. Некоторые пытаются связать узел с Соломоном, переводя еврейское слово פקעים, которое упомянуто в Библии. Однако, в более принятом переводе это слово означает «орнамент в виде тыквы». В Африке узел Соломона найден на тканях, расшитых стеклянным бисером. Когда узел появляется в этой культуре, он часто означает королевский статус, так что он используется в коронах, мантиях и других церемониальных объектах. В Африке узел также найден на вельвете касаи, сотканной из волокна пальм рафия одежды народа куба. Они приписывают узлу мистический смысл, как и народ акан в Западной Африке, которые печатают узел на святой одежде Адинкра. В Латвии, когда узел Соломона используется на текстиле или металлических изделиях, он ассоциируется со временем, движением и могуществом древних языческих богов. В современной науке некоторые версии стилизованных обозначений атома (электронные орбиты) являются вариантами узла Соломона. Логотипом программного обеспечения Joomla! является узел Соломона. См. такжеправитьПримечанияправить
Литератураправить
Seeing Solomon’s Knot, With Photographs by Joel Lipton, Lois Rose Rose, Los Angeles, 2005 (официальный сайт https://web.archive.org/web/20160310205443/http://stoneandscott.com/solomonsknot.asp). Несколько археологических отчётов, книг по искусству, профессиональных руководств, музейных каталогов, аукционных каталогов, путеводителей и религиозных документов, в которых обсуждается рисунок узла Соломона:
Ссылкиправить
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||