Край многообразия
Край многообра́зия — множество всех точек -мерного многообразия , которые не имеют окрестности, гомеоморфной -мерному евклидову пространству [1].

Более формально, край многообразия — подмножество замыкания вещественного -мерного многообразия (возможно, открытого) такое, что некоторая окрестность каждой точки этого подмножества гомеоморфна некоторой области некоторого замкнутого полупространства вещественного -мерного пространства , причём эта область открыта в полупространстве , но не во всём пространстве [2].
Краевая точка области — точка пересечения с границей полупространства [2].
Краевая точка многообразия — точка , которая соответствует краевой точке области [2]. Другими словами, точка -мерного многообразия , которая не имеет окрестности, гомеоморфной -мерному евклидову пространству [1].
Внутренняя точка многообразия — точка -мерного многообразия , которая имеет окрестность, гомеоморфную -мерному евклидову пространству [1].
Внутренность, или внутренняя часть, многообра́зия — множество всех внутренних точек -мерного многообразия [1].
Многообразие с краем — многообразие, имеющее хотя бы одну краевую точку[2].
Простейший пример -мерного многообразия с краем — полупространство [3].
На рисунке справа вверху показано некоторое подковообразное двумерное многообразие с одномерным краем , который состоит из двух окружностей , операцией взятия края и тремя гомеоморфизмами:
- окрестности внутренней точки многообразия на внутренность круга ;
- окрестности краевой точки многообразия на внутренность полукруга с диаметром ;
- окрестности точки многообразия на отрытый интервал .
Замкнутое многообразие — компактное многообразие без края[2].
Предложение 1. Замкнутое множество всех краевых точек вещественного -мерного многообразия есть -мерное многообразие без края, а разность множеств , которое есть всюду плотное открытое множество, — -мерное многообразие без края[2][3][4].
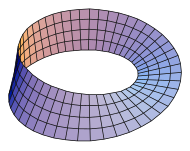
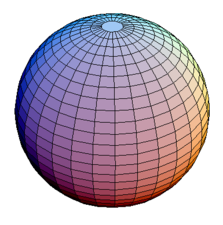
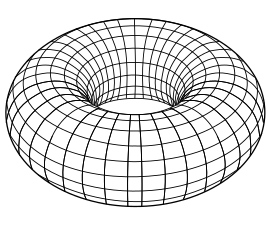
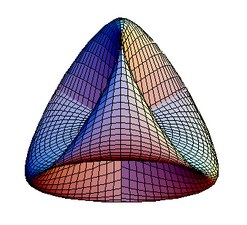
- Примеры замкнутых многообразий
Примечания
править- ↑ 1 2 3 4 Рохлин В. А., Фукс Д. Б. Начальный курс топологии. Геометрические главы, 1977, Глава 3. Гладкие многообразия. § 1. Основные понятия. 1. Топологические многообразия, с. 131.
- ↑ 1 2 3 4 5 6 Войцеховский М. И. Край, 1982.
- ↑ 1 2 Борисович, Ю. Г., Близняков Н. М., Израилевич Я. А., Фоменко Т. Н. Введение в топологию, 2015, Глава 4. Многообразия и расслоения. § 3. Гладкие многообразия. 11. Многообразия с краем, с. 230.
- ↑ Рохлин В. А., Фукс Д. Б. Начальный курс топологии. Геометрические главы, 1977, Глава 3. Гладкие многообразия. § 1. Основные понятия. 1. Топологические многообразия, с. 131—132.
Источники
править- Борисович, Ю. Г., Близняков Н. М., Израилевич Я. А., Фоменко Т. Н. Введение в топологию: Учебное пособие. Изд. 3-е, испр. и доп. М.: ЛЕНАНД, 2015. 441 с., ил. (Классический учебник МГУ.)
- Войцеховский М. И. Край // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 3 Коо—Од. М.: «Советская Энциклопедия», 1982. 1184 стб., ил. Стб. 87.
- Рохлин В. А., Фукс Д. Б. Начальный курс топологии. Геометрические главы. М.: «Наука», 1977. 487 с., ил.
Статья является кандидатом в добротные статьи с 5 ноября 2024. |