Число отрезков — инвариант узла, определяющий наименьшее число прямых «отрезков», которые, соединяясь конец к концу, образуют узел. Говоря более строго, числом отрезков геометрического узла называется число звеньев в минимальной по числу звеньев ломаной, лежащей в и объемлюще-изотопной геометрическому узлу . Данная функция на множестве всех геометрических узлов по определению постоянна на объемлюще-изотопических классах геометрических узлов, а значит можно говорить о числе отрезков как об инварианте узла. Число отрезков узла обозначается через .[1][2]
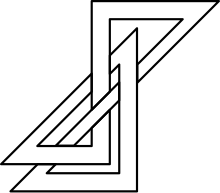
Известные значения
правитьНаименьшее число отрезков для нетривиального узла равно . Число отрезков, как и прочие меры сложности узлов, трудновычислимы, поэтому известно не так много точных значений[3]. В 1997 году Гё Тэк Чин определил[4] число отрезков торического узла для близких :
- , если ,
- , если ,
- , если .
Подобный результат, но для меньшей области параметров, примерно в то же время независимо получила исследовательская группа, возглавляемая Колином Адамсом[англ.][5]. Им, например, удалось доказать, что:
- , если .
Если — произвольная связная сумма, состоящая из трилистников (не обязательно только левых или только правых), то[5]:
- .
Оценки
правитьЧисло отрезков связной суммы узлов ограничено сверху суммой чисел отрезков слагаемых, а более точно[4][5]:
- .
Если и — взаимно простые целые числа, причем , то[4]:
- .
Связанные инварианты
правитьЧисло отрезков узла связано с его числом перекрёстков следующим неравенством[6][7][8]:
- .
Примечания
править- ↑ Adams, 2004, p. 29.
- ↑ Adams, Flapan, Henrich, Kauffman, Ludwig, Nelson, 2020, p. 833.
- ↑ Adams, Flapan, Henrich, Kauffman, Ludwig, Nelson, 2020, «There are very few infinite families of knots for which we know the stick number», p. 834.
- ↑ 1 2 3 Jin, 1997.
- ↑ 1 2 3 Adams, Brennan, Greilsheimer, Woo, 1997.
- ↑ Negami, 1991.
- ↑ Calvo, 2001.
- ↑ Huh, Oh, 2011.
Литература
править- Adams C. C. The Knot Book. An Elementary Introduction to the Mathematical Theory of Knots (англ.). — New York: American Mathematical Society, 2004. — 307 p. — ISBN 978-0821836781.
- Adams C. C., Flapan, E., Henrich, A., Kauffman, L. H., Ludwig, L. D., Nelson, S. Encyclopedia of Knot Theory (англ.). — Chapman and Hall/CRC, 2020. — 954 p. — ISBN 978-1138297845.
- Adams C. C., Brennan B. M., Greilsheimer D. L., Woo A. K. Stick numbers and composition of knots and links (англ.) // Journal of Knot Theory and its Ramifications. — 1997. — Vol. 6, iss. 2. — P. 149—161. — doi:10.1142/S0218216597000121.
- Calvo J. A. Geometric knot spaces and polygonal isotopy (англ.) // Journal of Knot Theory and its Ramifications. — 2001. — Vol. 10, iss. 2. — P. 245—267. — doi:10.1142/S0218216501000834.
- Jin G. T. Polygon indices and superbridge indices of torus knots and links (англ.) // Journal of Knot Theory and its Ramifications. — 1997. — Vol. 6, iss. 2. — P. 281—289. — doi:10.1142/S0218216597000170.
- Negami S. Ramsey theorems for knots, links and spatial graphs (англ.) // Transactions of the American Mathematical Society. — 1991. — Vol. 324, iss. 2. — P. 527—541. — doi:10.2307/2001731.
- Huh Y., Oh S. An upper bound on stick number of knots (англ.) // Journal of Knot Theory and its Ramifications. — 2011. — Vol. 20, iss. 5. — P. 741—747. — doi:10.1142/S0218216511008966.
Ссылки
править- Weisstein, Eric W. Stick number (англ.) на сайте Wolfram MathWorld.
- «Stick numbers for minimal stick knots», KnotPlot Research and Development Site.
- Adams C. C. Why knot: knots, molecules and stick numbers // Plus Magazine. — 2005.



