Торический узел

Торический узел — специальный вид узлов, лежащих на поверхности незаузлённого тора в $\mathbb {R} ^{3}$.

(3,7)-торический узел.

Приз EureleA в виде (2,3)-торического узла.

(2,8)-торическое зацепление

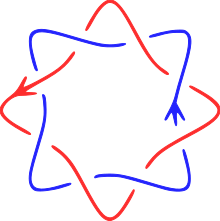
Торическое зацепление — зацепление, лежащее на поверхности тора. Каждый торический узел определяется парой взаимно простых целых чисел $p$ и $q$. Торическое зацепление возникает, когда $p$ и $q$ не взаимно просты (в этом случае число компонент равно наибольшему общему делителю $p$ и $q$). Торический узел является тривиальным тогда и только тогда, когда либо $p$, либо $q$ равны 1 или −1. Простейшим нетривиальным примером является (2,3)-торический узел, известный также как трилистник.

(2,−3)-торический узел, известный также как левый трилистник

Геометрическое представление

Торический узел можно представить геометрически различными способами, топологически эквивалентными, но геометрически различными.

Обычно используется соглашение, что $(p,q)$-торический узел вращается $q$ раз вокруг круговой оси тора и $p$ раз вокруг оси вращения тора. Если $p$ и $q$ не взаимно просты, то получается торическое зацепление, имеющее более одной компоненты. Соглашения о направлении, в котором нити вращаются вокруг тора, также различны, чаще всего предполагается правый винт для $pq>0$.

$(p,q)$-торический узел может быть задан параметризацией:

$x=r$ $\cos(p\phi )$,

$y=r$ $\sin(p\phi )$,

$z=-\sin(q\phi )$,

где $r=\cos(q\phi )+2$ и $0<\phi <2\pi$. Он лежит на поверхности тора, задаваемого формулой $(r-2)^{2}+z^{2}=1$ (в цилиндрических координатах).

Возможны и другие параметризации, поскольку узлы определены с точностью до непрерывной деформации. Примеры для (2,3)- и (3,8)-торических узлов можно получить, приняв $r=\cos(q\phi )+4$, а в случае (2,3)-торического узла путём вычитания $3\cos((p-q)\phi )$ и $3\sin((p-q)\phi )$ из вышеприведённых параметризаций $x$ и $y$.

Свойства

Диаграмма (3,−8)-торического узла.

Торический узел является тривиальным тогда и только тогда, когда либо $p$, либо $q$ равны 1 или −1.

Каждый нетривиальный торический узел является простым и хиральными.

$(p,q)$-торический узел эквивалентен $(q,p)$-торическому узлу. $(p,-q)$-торический узел является обратным (зеркальным отражением) $(p,q)$-торического узла. $(-p,-q)$-торический узел эквивалентен $(p,q)$-торическому узлу, за исключением ориентации.

(3, 4) торический узел на развороте поверхности тора и слово косы

Любой $(p,q)$-торический узел может быть построен из замкнутой косы с $p$ нитями. Подходящее слово косы:

$(\sigma _{1}\sigma _{2}\cdots \sigma _{p-1})^{q}$.

Эта формула использует соглашение, что генераторы косы используют правые вращения.

Число пересечений $(p,q)$-торического узла с $p,q>0$ задаётся формулой:

$c=\min((p-1)q,(q-1)p)$.

Род торического узла с $p,q>0$ равен:

$g={\frac {1}{2}}(p-1)(q-1).$

Многочлен Александера торического узла равен:

${\frac {(t^{pq}-1)(t-1)}{(t^{p}-1)(t^{q}-1)}}$.

Полином Джонса (правовинтовой) торического узла задаётся формулой:

$t^{(p-1)(q-1)/2}{\frac {1-t^{p+1}-t^{q+1}+t^{p+q}}{1-t^{2}}}$.

Дополнение торического узла на 3-сфере — это многообразие Зейферта.

Пусть $Y$ — $p$-мерный дурацкий колпак с диском, удалённым внутри, $Z$ — $q$-мерный дурацкий колпак с внутренним удалённым диском, и $X$ — факторпространство, полученное отождествлением $Y$ и $Z$ вдоль границы окружности. Дополнение $(p,q)$-торического узла является деформационным ретрактом пространства $X$. Таким образом, группа узла торического узла имеет представление:

$\langle x,y\mid x^{p}=y^{q}\rangle$.

Торические узлы — это единственные узлы, чьи группы узла имеют нетривиальные центры (которые являются бесконечными циклическими группами, образованные элементом $x^{p}=y^{q}$ из этого представления).

Список

• Тривиальный узел, 3₁-узел (2,3), Узел «Лапчатка» (5,2), 7₁-узел (7,2), 8₁₉-узел (4,3), 9₁-узел (9,2), 10₁₂₄-узел (5,3).

См. также

• Альтернированный узел
• Узел «Лапчатка»
• Иррациональное обвивание тора

Литература

• Charles Livingston. Knot theory. — Mathematical Association of America, 1993. — ISBN 0-88385-027-3.
• Kunio Murasugi. Knot theory and its applications. — Birkhäuser, 1996. — ISBN 3-7643-3817-2.
• Akio Kawauchi. A survey of knot theory. — Birkhäuser, 1996. — ISBN 3-7643-5124-1.
• W. B. R. Lickorish. An introduction to knot theory. — Springer, 1997. — ISBN 0-387-98254-X.
• J. S. Birman, T. E. Brendle. Handbook of knot theory / W. Menasco, M. Thistlethwaite. — Elsevier, 2005. — ISBN 0-444-51452-X..
• J. Milnor. Singular Points of Complex Hypersurfaces. — Princeton University Press, 1968. — ISBN 0-691-08065-8.

Ссылки

• 36 Torus Knots, The Knot Atlas.
• Weisstein, Eric W. Torus Knot (англ.) на сайте Wolfram MathWorld.
• Torus knot renderer in Actionscript
• Fun with the PQ-Torus Knot