Функция делителей

Фу́нкция дели́телей — арифметическая функция, связанная с делителями целого числа. Функция известна также под именем фу́нкция диви́зоров. Применяется, в частности, при исследовании связи дзета-функции Римана и рядов Эйзенштейна для модулярных форм. Изучалась Рамануджаном, который вывел ряд важных равенств в модульной арифметике и арифметических тождествах.

Функция делителей от σ₀(n) до n = 250

Сигма-функция от σ₁(n) до n = 250

Сумма квадратов делителей, от σ₂(n), до n = 250

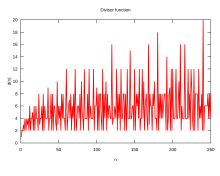
С этой функцией тесно связана суммирующая функция делителей, которая, как следует из названия, является суммой функции делителей.

Определение

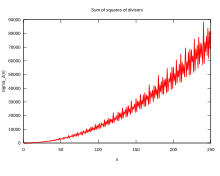
Функция «сумма положительных делителей» $\sigma _{z}(n)$ для вещественного или комплексного числа $n$ определяется как сумма $z$-х степеней положительных делителей числа n. Функцию можно выразить формулой

$\sigma _{z}(n)=\sum _{d|n}d^{z}\,\!,$

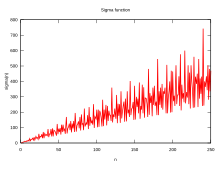
где ${d|n}$ означает «d делит n». Обозначения d(n), ν(n) и τ(n) (от немецкого Teiler = делитель) используются также для обозначения σ₀(n), или функции числа делителей . Если z равен 1, функция называется сигма-функцией или суммой делителей, и индекс часто опускается, так что σ(n) эквивалентна σ₁(n).

Аликвотная сумма s(n) для n — это сумма собственных делителей (то есть всех делителей, за исключением самого n, и равна σ₁(n) − n. Аликвотная последовательность для n образуется последовательным вычислением аликвотной суммы, то есть каждое последующее значение в последовательности равно аликвотной сумме предыдущего значения.

Примеры

Например, σ₀(12) — количество делителей числа 12:

${\begin{aligned}\sigma _{0}(12)&=1^{0}+2^{0}+3^{0}+4^{0}+6^{0}+12^{0}\\&=1+1+1+1+1+1=6,\end{aligned}}$

в то время как σ₁(12) — сумма всех делителей:

${\begin{aligned}\sigma _{1}(12)&=1^{1}+2^{1}+3^{1}+4^{1}+6^{1}+12^{1}\\&=1+2+3+4+6+12=28,\end{aligned}}$

и аликвотная сумма s(12) собственных делителей равна:

${\begin{aligned}s(12)&=1^{1}+2^{1}+3^{1}+4^{1}+6^{1}\\&=1+2+3+4+6=16.\end{aligned}}$

Таблица значений

n	Делители	σ0(n)	σ1(n)	s(n) = σ1(n) − n	Комментарии
1	1	1	1	0	квадрат: значение σ0(n) нечётно; степень 2: s(n) = n − 1 (почти совершенное)
2	1,2	2	3	1	простое: σ1(n) = 1+n, так что s(n) =1
3	1,3	2	4	1	простое: σ1(n) = 1+n, так что s(n) =1
4	1,2,4	3	7	3	квадрат: σ0(n) нечётно; степень 2: s(n) = n − 1 (почти совершенное)
5	1,5	2	6	1	простое: σ1(n) = 1+n, так что s(n) =1
6	1,2,3,6	4	12	6	первое совершенное число: s(n) = n
7	1,7	2	8	1	простое: σ1(n) = 1+n, так что s(n) =1
8	1,2,4,8	4	15	7	степень 2: s(n) = n − 1 (почти совершенное)
9	1,3,9	3	13	4	квадрат: σ0(n) нечётно
10	1,2,5,10	4	18	8
11	1,11	2	12	1	простое: σ1(n) = 1+n, так что s(n) =1
12	1,2,3,4,6,12	6	28	16	первое избыточное число: s(n) > n
13	1,13	2	14	1	простое: σ1(n) = 1+n, так что s(n) =1
14	1,2,7,14	4	24	10
15	1,3,5,15	4	24	9
16	1,2,4,8,16	5	31	15	квадрат: σ0(n) нечётно; степень 2: s(n) = n − 1 (почти совершенное)

Случаи $x=2$, $x=3$ и так далее входят в последовательности A001157, A001158, A001159, A001160, A013954, A013955 …

Свойства

Для целых, не являющихся квадратами, каждый делитель d числа n имеет парный делитель n/d, а значит, $\sigma _{0}(n)$ всегда чётно для таких чисел. Для квадратов один делитель, а именно ${\sqrt {n}}$, не имеет пары, так что для них $\sigma _{0}(n)$ всегда нечётно.

Для простого числа p,

${\begin{aligned}\sigma _{0}(p)&=2\\\sigma _{0}(p^{n})&=n+1\\\sigma _{1}(p)&=p+1\end{aligned}}$

поскольку, по определению, простое число делится только на единицу и самого себя. Если p_n# означает праймориал, то

$\sigma _{0}(p_{n}\#)=2^{n}$

Ясно, что $1<\sigma _{0}(n)<n$ и $\sigma (n)>n$ для всех $n>2$.

Функция делителей мультипликативна, но не вполне мультипликативна.

Если мы запишем

$n=\prod _{i=1}^{r}p_{i}^{a_{i}}$,

где r = ω(n) — число простых делителей числа n, p_i — i-й простой делитель, а a_i — максимальная степень p_i, на которую делится n, то

$\sigma _{x}(n)=\prod _{i=1}^{r}{\frac {p_{i}^{(a_{i}+1)x}-1}{p_{i}^{x}-1}}$,

что эквивалентно:

$\sigma _{x}(n)=\prod _{i=1}^{r}\sum _{j=0}^{a_{i}}p_{i}^{jx}=\prod _{i=1}^{r}(1+p_{i}^{x}+p_{i}^{2x}+\cdots +p_{i}^{a_{i}x}).$

Если положить x = 0, получим, что d(n) равно:

$\sigma _{0}(n)=\prod _{i=1}^{r}(a_{i}+1).$

Например, число n = 24 имеет два простых делителя — p₁ = 2 и p₂ = 3. Поскольку 24 — это произведение 2³×3¹, то a₁ = 3 и a₂ = 1.

Теперь мы можем вычислить $\sigma _{0}(24)$:

${\begin{aligned}\sigma _{0}(24)&=\prod _{i=1}^{2}(a_{i}+1)\\&=(3+1)(1+1)=4\times 2=8.\end{aligned}}$

Восемь делителей числа 24 — это 1, 2, 4, 8, 3, 6, 12, и 24.

Заметим также, что s(n) = σ(n) − n. Здесь s(n) обозначает сумму собственных делителей числа n, то есть делителей, за исключением самого числа n. Эта функция используется для определения совершенности числа — для них s(n) = n. Если s(n) > n, n называется избыточным, а если s(n) < n, n называется недостаточным.

Если n — степень двойки, то есть $n=2^{k}$, то $\sigma (n)=2\times 2^{k}-1=2n-1,$ и s(n) = n — 1, что делает n почти совершенным.

Как пример, для двух простых p и q (где p < q), пусть

$n=pq.$

Тогда

$\sigma (n)=(p+1)(q+1)=n+1+(p+q),$

$\phi (n)=(p-1)(q-1)=n+1-(p+q),$

и

$n+1=(\sigma (n)+\phi (n))/2,$

$p+q=(\sigma (n)-\phi (n))/2,$

где φ(n) — функция Эйлера.

Тогда корни p и q уравнения:

$(x-p)(x-q)=x^{2}-(p+q)x+n=x^{2}-[(\sigma (n)-\phi (n))/2]x+[(\sigma (n)+\phi (n))/2-1]=0$

можно выразить через σ(n) и φ(n) :

$p=(\sigma (n)-\phi (n))/4-{\sqrt {[(\sigma (n)-\phi (n))/4]^{2}-[(\sigma (n)+\phi (n))/2-1]}},$

$q=(\sigma (n)-\phi (n))/4+{\sqrt {[(\sigma (n)-\phi (n))/4]^{2}-[(\sigma (n)+\phi (n))/2-1]}}.$

Зная n и либо σ(n), либо φ(n) (или зная p+q и либо σ(n), либо φ(n)) мы легко можем найти p и q.

В 1984 году Хиз-Браун (Roger Heath-Brown) доказал, что

$\sigma _{0}(n)=\sigma _{0}(n+1)$

встречается бесконечно много раз.

Связь с рядами

Два ряда Дирихле, использующие функцию делителей:

$\sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)}{n^{s}}}=\zeta (s)\zeta (s-a),$

и при обозначении d(n) = σ₀(n) получим

$\sum _{n=1}^{\infty }{\frac {d(n)}{n^{s}}}=\zeta ^{2}(s),$

и второй ряд,

$\sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)\sigma _{b}(n)}{n^{s}}}={\frac {\zeta (s)\zeta (s-a)\zeta (s-b)\zeta (s-a-b)}{\zeta (2s-a-b)}}.$

Ряд Ламбера, использующий функцию делителей:

$\sum _{n=1}^{\infty }q^{n}\sigma _{a}(n)=\sum _{n=1}^{\infty }{\frac {n^{a}q^{n}}{1-q^{n}}}$

для любого комплексного |q| ≤ 1 и a.

Эта сумма появляется также в рядах Фурье для рядов Эйзенштейна и в инвариантах эллиптических функций Вейерштрасса.

Асимптотическая скорость роста

В терминах о-малое функция делителей удовлетворяет неравенству (см. стр. 296 книги Апостола)

для всех $\epsilon >0,\quad d(n)=o(n^{\epsilon }).$

Северин Вигерт дал более точную оценку

$\limsup _{n\to \infty }{\frac {\log d(n)}{\log n/\log \log n}}=\log 2.$

С другой стороны, ввиду бесконечности количества простых чисел,

$\liminf _{n\to \infty }d(n)=2.$

В терминах О-большое, Дирихле показал, что средний порядок функции делителей удовлетворяет следующему неравенству (см. теорему 3.3 книги Апостола)

для всех $x\geq 1,\sum _{n\leq x}d(n)=x\log x+(2\gamma -1)x+O({\sqrt {x}}),$

где $\gamma$ — постоянная Эйлера — Маскерони.

Задача улучшить границу $O({\sqrt {x}})$ в этой формуле — это проблема Дирихле о делителях

Поведение сигма-функции неравномерно. Асимптотическую скорость роста сигма-функции можно выразить формулой:

$\limsup _{n\rightarrow \infty }{\frac {\sigma (n)}{n\,\log \log n}}=e^{\gamma },$

где lim sup — верхний предел. Этот результат является теоремой Грёнвалла (Grönwall), опубликованной в 1913 году. Его доказательство использует третью теорему Мертенса, которая утверждает, что

$\lim _{n\to \infty }{\frac {1}{\log n}}\prod _{p\leq n}{\frac {p}{p-1}}=e^{\gamma },$

где p — простое.

В 1915 году Рамануджан доказал, что при выполнении гипотезы Римана неравенство

$\ \sigma (n)<e^{\gamma }n\ln \ln n$ (неравенство Робина)

выполняется для всех достаточно больших n. В 1984 году Гай Робин доказал, что неравенство верно для всех n ≥ 5041 в том и только в том случае, если гипотеза Римана верна. Это теорема Робина и неравенство стало широко известно после доказательства теоремы. Наибольшее известное число, нарушающее неравенство — это n=5040. Если гипотеза Римана верна, то нет чисел, больших этого и нарушающих неравенство. Робин показал, что в случае ошибочности гипотезы существует бесконечно много чисел n, нарушающих неравенство, и известно, что наименьшее из таких чисел n ≥ 5041 должно быть сверхизбыточным числом. Было показано, что неравенство выполняется для больших нечётных свободных от квадратов чисел, и что гипотеза Римана эквивалентна выполнению неравенства для всех чисел n, делящихся на пятую степень простого числа

Джефри Лагариас (Jeffrey Lagarias) в 2002 году доказал, что гипотеза Римана эквивалентна утверждению

$\sigma (n)\leq H_{n}+\ln(H_{n})e^{H_{n}}$

для любого натурального n, где $H_{n}$ — n-е гармоническое число.

Робин доказал, что неравенство

$\ \sigma (n)<e^{\gamma }n\ln \ln n+{\frac {0.6483\ n}{\ln \ln n}}$

выполняется для n ≥ 3 без каких-либо дополнительных условий.

Ссылки

• Bach, Eric; Shallit, Jeffrey, Algorithmic Number Theory, volume 1, 1996, MIT Press. ISBN 0-262-02405-5, see page 234 in section 8.8.
• Weisstein, Eric W. Robin's Theorem (англ.) на сайте Wolfram MathWorld.
• Elementary Evaluation of Certain Convolution Sums Involving Divisor Functions PDF, авторы — Huard, Ou, Spearman, и Williams. Содержит элементарное (то есть не опирающееся на теорию модулярных форм) доказательство свертки суммы делителей, формулы для представления различными способами чисел как суммы треугольных чисел.