В математике n-м гармоническим числом называется сумма обратных величин первых n последовательных чисел натурального ряда:
Гармонические числа являются частичными суммами гармонического ряда.
Изучение гармонических чисел началось в античности. Они имеют важное значение в различных областях теории чисел и теории алгоритмов и, в частности, тесно связаны с дзета-функцией Римана.
Альтернативные определения
править- Гармонические числа можно определить рекуррентно следующим образом:
- Также верно соотношение:
- ,
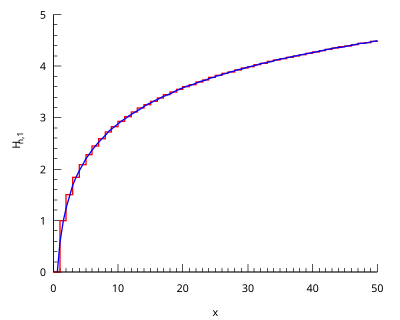
- где — дигамма-функция, — постоянная Эйлера — Маскерони.
- Еще соотношения:
- где в точке - верхняя конечная разность n-го порядка функции .
Дополнительные представления
правитьНижеследующие формулы могут быть использованы для вычисления гармонических чисел (в том числе и в точках, отличных от точек натурального ряда):
- интегральные представления:
- предельные представления:
- ;
- разложение в ряд Тейлора в точке :
- где — дзета-функция Римана;
- асимптотическое разложение:
- .
Производящая функция
править
Свойства
правитьЗначения от нецелого аргумента
править- где — золотое сечение.
Суммы, связанные с гармоническими числами
правитьТождества, связанные с гармоническими числами
править- , где
- , где
Приближённое вычисление
правитьС помощью формулы суммирования Эйлера-Маклорена получаем следующую формулу:
где , — постоянная Эйлера, которую можно вычислить быстрее из других соображений[каких?], а — числа Бернулли.
Теоретико-числовые свойства
править- Теорема Вольстенхольма утверждает, что для всякого простого числа выполняется сравнение:
Некоторые значения гармонических чисел
правитьЧислитель и знаменатель несократимой дроби, представляющей собой n-e гармоническое число, являются n-ми членами целочисленных последовательностей A001008 и A002805, соответственно.
Приложения
правитьВ 2002 году Lagarias доказал[1], что гипотеза Римана о нулях дзета-функции Римана эквивалентна утверждению, что неравенство
верно при всех целых со строгим неравенством при , где — сумма делителей числа .
См. также
правитьПримечания
править- ↑ Jeffrey Lagarias. An Elementary Problem Equivalent to the Riemann Hypothesis // Amer. Math. Monthly. — 2002. — № 109. — С. 534-543. Архивировано 27 июня 2021 года.
Для улучшения этой статьи желательно:
|



