Функция Эйлера
Фу́нкция Э́йлера — мультипликативная арифметическая функция, значение которой равно количеству натуральных чисел, меньших или равных и взаимно простых с ним[1].
Например, для числа 36 существует 12 меньших его и взаимно простых с ним чисел (1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35), поэтому .
Названа в честь Эйлера, который впервые использовал её в 1763 году в своих работах по теории чисел для доказательства малой теоремы Ферма, а затем и для доказательства более общего утверждения — теоремы Эйлера. Позднее функцию использовал Гаусс в своем труде «Арифметические исследования», вышедшем в свет в 1801 году. Гаусс ввёл ставшее стандартным обозначение [2].
Функция Эйлера находит применение в вопросах, касающихся теории делимости и вычетов (см. сравнение по модулю), теории чисел, криптографии. Функция Эйлера играет ключевую роль в алгоритме RSA[3].
Вычисление
править| +0 | +1 | +2 | +3 | +4 | +5 | +6 | +7 | +8 | +9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0+ | 1 | 1 | 2 | 2 | 4 | 2 | 6 | 4 | 6 | |
| 10+ | 4 | 10 | 4 | 12 | 6 | 8 | 8 | 16 | 6 | 18 |
| 20+ | 8 | 12 | 10 | 22 | 8 | 20 | 12 | 18 | 12 | 28 |
| 30+ | 8 | 30 | 16 | 20 | 16 | 24 | 12 | 36 | 18 | 24 |
| 40+ | 16 | 40 | 12 | 42 | 20 | 24 | 22 | 46 | 16 | 42 |
| 50+ | 20 | 32 | 24 | 52 | 18 | 40 | 24 | 36 | 28 | 58 |
| 60+ | 16 | 60 | 30 | 36 | 32 | 48 | 20 | 66 | 32 | 44 |
| 70+ | 24 | 70 | 24 | 72 | 36 | 40 | 36 | 60 | 24 | 78 |
| 80+ | 32 | 54 | 40 | 82 | 24 | 64 | 42 | 56 | 40 | 88 |
| 90+ | 24 | 72 | 44 | 60 | 46 | 72 | 32 | 96 | 42 | 60 |
Общие сведения
правитьФункция Эйлера показывает, сколько натуральных чисел из отрезка имеют c только один общий делитель — единицу. Функция Эйлера определена на множестве натуральных чисел, и значения её лежат во множестве натуральных чисел.
Как следует из определения, чтобы вычислить , нужно перебрать все числа от до , и для каждого проверить, имеет ли оно общие делители с , а затем подсчитать, сколько чисел оказались взаимно простыми с . Эта процедура для больших чисел весьма трудоёмка, поэтому для вычисления используют другие методы, которые основываются на специфических свойствах функции Эйлера.
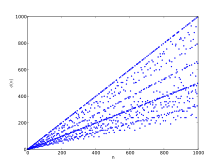
В таблице справа представлены первые 99 значений функции Эйлера. Значение при не превосходит , и в точности ему равно, если — простое. Таким образом, если в координатах провести прямую , то значения будут лежать либо на этой прямой, либо ниже её. Также, глядя на график, приведенный в начале статьи, и на значения в таблице, можно предположить, что существует прямая, проходящая через ноль, которая ограничивает значения снизу. Однако, оказывается, такой прямой не существует. То есть, какую бы пологую прямую мы ни провели, всегда найдется натуральное число , такое, что лежит ниже этой прямой. Ещё одной интересной особенностью графика является наличие некоторых прямых, вдоль которых концентрируются значения функции Эйлера. Так, например, помимо прямой , на которой лежат значения , где — простое, выделяется прямая, примерно соответствующая , на которую попадают значения , где — простое.
Более подробно поведение функции Эйлера рассматривается в разделе #Асимптотические соотношения.
Мультипликативность функции Эйлера
правитьОдним из основных свойств функции Эйлера является её мультипликативность. Это свойство было установлено ещё Эйлером и формулируется оно следующим образом: для любых взаимно простых чисел и [5]
Для доказательства мультипликативности функции Эйлера потребуется следующая вспомогательная теорема[6].
- Теорема 1. Пусть и пробегает полную систему вычетов по модулю , в то время как пробегает полную систему вычетов по модулю . Тогда числа образуют полную систему вычетов по модулю .
- Доказательство. Если
- тогда
- поэтому
- аналогично
- Поэтому существует несравнимых по модулю чисел, которые образуют полную систему вычетов по модулю .
Теперь можно доказать основное утверждение[7].
- Теорема 2. Функция Эйлера мультипликативна.
- Доказательство. Если , то по Теореме 1 пробегает приведённую систему вычетов по модулю , когда и пробегают приведённые системы вычетов по модулям и соответственно. Также:
- Поэтому чисел, которые меньше числа и взаимно просты с ним, являются наименьшими положительными вычетами среди значений , для которых взаимно просто с и взаимно просто с . Отсюда следует, что
Функция Эйлера от простого числа
правитьДля простого значение функции Эйлера задаётся явной формулой[8]:
которая следует из определения. Действительно, если — простое, то все числа, меньшие , взаимно просты с ним, а их ровно штук.
Для вычисления функции Эйлера от степени простого числа используют следующую формулу[8]:
Это равенство обосновывается следующим образом. Подсчитаем количество чисел от до , которые не взаимно просты с . Все они, очевидно, кратны , то есть, имеют вид: Всего таких чисел . Поэтому количество чисел, взаимно простых с , равно .
Функция Эйлера от натурального числа
правитьВычисление для произвольного натурального основывается на мультипликативности функции Эйлера, выражении для , а также на основной теореме арифметики. Для произвольного натурального числа значение представляется в виде[8]:
где — простое число и пробегает все значения, участвующие в разложении на простые сомножители.
Как следует из основной теоремы арифметики, всякое натуральное число единственным образом представляется в виде:
где — простые числа, — натуральные числа.
Используя мультипликативность функции Эйлера и выражение для , получаем:
Пример применения:
Свойства
правитьОбобщённая мультипликативность
правитьФункция Эйлера является мультипликативной арифметической функцией, то есть
Здесь существенно, что наибольший общий делитель и равен единице. Оказывается, существует обобщение этой формулы на случай, когда и имеют общие делители, отличные от единицы. А именно, для любых натуральных и [9]:
где — наибольший общий делитель и Это свойство является естественным обобщением мультипликативности.
Пусть тогда причем в общем случае и Поэтому можно записать:
Здесь первые делителей являются также делителями а последние делителей являются делителями Распишем:
В силу мультипликативности функции Эйлера, а также с учётом формулы
где — простое, получаем:
В первой строке записано во второй — а третью можно представить, как Поэтому:
Некоторые частные случаи:
- где — наименьшее общее кратное и , а — их наибольший общий делитель.
Теорема Эйлера
правитьНаиболее часто на практике используется свойство, установленное Эйлером:
если и взаимно просты.
Это свойство, которое называют теоремой Эйлера, вытекает из Теоремы Лагранжа и того факта, что равна порядку мультипликативной группы обратимых элементов кольца вычетов по модулю .
В качестве следствия теоремы Эйлера можно получить малую теорему Ферма. Для этого нужно взять не произвольное а простое. Тогда:
Последняя формула находит применение в различных тестах простоты.
Другие свойства
правитьИсходя из представимости произведением Эйлера, несложно получить следующее полезное утверждение:
Следующее равенство[10][11] является следствием теоремы Зигмонди[англ.]:
Всякое натуральное число представимо в виде суммы значений функции Эйлера от его натуральных делителей[12]:
Сумма всех чисел, меньших данного, и взаимно простых с ним, выражается через функцию Эйлера:
Множество значений
правитьИсследование структуры множества значений функции Эйлера является отдельной сложной задачей. Здесь представлены лишь некоторые результаты, полученные в этой области[13].
- Функция Эйлера принимает только чётные значения при Причём, если имеет различных нечётных простых делителей, то
- Действительно, если — простое нечётное и то
- — чётное.
- Из равенства
- следует утверждение.
В действительном анализе часто возникает задача нахождения значения аргумента по заданному значению функции, или, другими словами, задача нахождения обратной функции. Подобную задачу можно поставить и для функции Эйлера. Однако, надо иметь в виду следующее.
- Значения функции Эйлера повторяются (например, ), следовательно обратная функция является многозначной.
- Функция Эйлера принимает лишь чётные значения при то есть если нечётно и
В связи с этим нужны особые методы анализа. Полезным инструментом для исследования прообраза является следующая теорема[14].
- Пусть — чётное, положим
- где — простое.
- Если то
- Очевидно, если то С другой стороны, если и то
- Однако, если то Поэтому
- Следовательно
Эта теорема показывает, что прообраз элемента всегда представляет собой конечное множество. Также она даёт следующий практический способ нахождения прообраза:
- 1) вычислить ;
- 2) вычислить для всех из полуинтервала ;
- 3) все числа для которых образуют прообраз элемента .
Может оказаться, что в указанном промежутке нет такого числа что в этом случае прообраз является пустым множеством.
Для вычисления нужно знать разложение на простые сомножители, что для больших является вычислительно сложной задачей. Затем нужно раз вычислить функцию Эйлера, что для больших чисел также весьма трудоёмко. Поэтому нахождение прообраза в целом является вычислительно сложной задачей.
Найдем прообраз 4. Делителями 4 являются числа 1, 2 и 4. Добавляя по единице к каждому из них, получаем 2, 3, 5 — простые числа. Вычисляем
Чтобы найти прообраз 4, достаточно рассмотреть числа от 5 до 15. Проделав выкладки, получим:
Не существует, например, такого числа что То есть:
В самом деле, делители 14 суть 1, 2, 7 и 14. Добавив по единице, получим 2, 3, 8, 15. Из них только первые два числа — простые. Поэтому
Перебрав все числа от 15 до 42, несложно убедиться, что
Асимптотические соотношения
правитьПростейшие неравенства
править- для всех кроме и
- для всякого составного
- Для всех натуральных значений справедливо двойное неравенство[15]:
Сравнение φ(n) с n
править- Верхняя грань отношения приближается к единице с ростом [18]:
- В то же время отношение может быть сколь угодно большим[19]:
Отношение последовательных значений
править- Следующие равенства показывают, насколько непредсказуемо ведет себя функция Эйлера[20]:
- и
- Формулы, приведенные выше, получил Somayajulu в 1950 году. А четырьмя годами позже Шинцель и Серпинский доказали[20], что множество
- плотно в множестве действительных положительных чисел.
- В том же году они установили[20], что множество
- плотно на интервале
Асимптотики для сумм
править- Точное выражение для суммы последовательных значений функции Эйлера[21]:
- Отсюда вытекает, что средний порядок[англ.] функции Эйлера равно . Этот результат интересен тем, что позволяет получить вероятность события, состоящего в том, что два наугад выбранных натуральных числа являются взаимно простыми. А именно, эта вероятность равна [22].
- С учётом приведённого выше выражения, можно получить следующие асимптотические оценки:
- ;
- .
- Используя мультипликативность функции Эйлера и свойства суммы делителей , несложно установить, что[23]
- .
Порядок функции Эйлера
править- Этот результат можно уточнить. В 1962 году была получена оценка снизу для функции Эйлера[26]:
- для всех , с одним исключением в указанном случае следует заменить на Это одна из наиболее точных оценок снизу для [27].
- В качестве оценки сверху был установлен следующий факт[28]: существует бесконечно много натуральных таких, что
- Как отмечает Пауло Рибенбойм[англ.] по поводу доказательства этого неравенства[27]: «Способ доказательства интересен тем, что неравенство сначала устанавливается в предположении, что гипотеза Римана верна, а затем в предположении, что она не верна».
Связь с другими функциями
правитьФункция Мёбиуса
править- Следующую формулу можно использовать для вычисления [29]:
- где — функция Мёбиуса.
- Другие соотношения с функцией Мёбиуса:
- [30].
Ряд Дирихле
править- Ряд Дирихле с коэффициентами можно представить через дзета-функцию Римана[31]:
Ряд Ламберта
править- Сумма ряда Ламберта с коэффициентами [32]:
Наибольший общий делитель
править- Функция Эйлера является дискретным преобразованием Фурье наибольшего общего делителя[33]:
- Действительная часть:
- В отличие от произведения Эйлера, вычисления по этим формулам не требуют знания делителей
Связь с латинскими квадратами
править- Число циклических латинских квадратов порядка с фиксированной первой строкой определяется функцией Эйлера . Данную особенность можно использовать при вычислении значения функции Эйлера путем подсчета соответствующего числа квадратов заданного порядка используя алгоритм без умножений и делений, однако асимптотически это медленнее, чем расчет на базе факторизации аргумента . Циклические диагональные латинские квадраты являются подмножеством циклических латинских квадратов, поэтому число циклических диагональных латинских квадратов с фиксированной первой строкой (последовательность A123565 в OEIS) является ограничением снизу на значение функции Эйлера [34].
Приложения и примеры
правитьФункция Эйлера в RSA
правитьНа основе алгоритма, предложенного в 1978 году Рональдом Ривестом, Ади Шамиром и Леонардом Адлеманом, была построена первая система шифрования с открытым ключом, получившая название по первым буквам фамилий авторов — система RSA. Криптостойкость этой системы определяется сложностью разложения на сомножители целого -разрядного числа. Ключевую роль в алгоритме RSA играет функция Эйлера, свойства которой и позволяют построить криптографическую систему с открытым ключом[35].
На этапе создания пары из секретного и открытого ключей вычисляется
где и — простые. Затем выбираются случайные числа так, чтобы
Затем сообщение шифруется открытым ключом адресата:
После этого расшифровать сообщение может только обладатель секретного ключа :
Корректность последнего утверждения основывается на теореме Эйлера и китайской теореме об остатках.
В силу выбора чисел на этапе создания ключей
Если то, с учетом теоремы Эйлера,
В общем случае и могут иметь общие делители, но расшифрование всё равно оказывается верным. Пусть По китайской теореме об остатках:
Подставляя получаем тождество
Следовательно,
Вычисление обратного элемента
правитьФункция Эйлера может быть использована для вычисления обратного по умножению элемента по модулю , а именно[36]:
- если
Эта формула следует из теоремы Эйлера:
Найдем , то есть такое число , что
Очевидно, и не имеют общих делителей кроме единицы, , при этом число простое и
поэтому удобно воспользоваться формулой, приведенной выше:
Легко проверить, что в самом деле
В общем случае для вычисления обратных значений алгоритм Евклида быстрее, чем использование теоремы Эйлера[37], так как битовая сложность вычисления по алгоритму Евклида имеет порядок в то время как вычисление по теореме Эйлера требует порядка битовых операций, где Однако, в случае, когда известно разложение на простые сомножители, сложность вычислений можно уменьшить, используя алгоритмы быстрого возведения в степень: Алгоритм Монтгомери или алгоритм «возводи в квадрат и перемножай»[38].
Если то обратного к элемента не существует, или, иначе говоря, уравнение
не имеет решения на множестве натуральных чисел[39].
Доказательство. В самом деле, допустим
и решение существует. Тогда по определению наибольшего общего делителя
- причем
поэтому можно записать:
- где
или, перегруппировав слагаемые,
Слева стоит целое отличное от нуля число, значит и справа должно быть целое отличное от нуля число, поэтому с необходимостью
что противоречит предположению.
Решение линейного сравнения
правитьМетод вычисления обратного элемента можно использовать для решения сравнения
Решение задаётся формулой[37]:
- если
Рассмотрим сравнение
Так как можно воспользоваться указанной формулой:
Подстановкой убеждаемся, что
Если , сравнение либо имеет не единственное решение, либо не имеет решения. Как легко убедиться, сравнение
не имеет решения на множестве натуральных чисел. В то же время сравнение
имеет два решения
Вычисление остатка от деления
правитьФункции Эйлера позволяет вычислять остатки от деления больших чисел[40].
Найдем последние три цифры в десятичной записи числа Замечая, что
получаем
Переходя теперь от модуля к модулю имеем:
Следовательно, десятичная запись числа оканчивается на
Найдем остаток от деления на Легко видеть, что
Поэтому, воспользовавшись мультипликативностью функции Эйлера и равенством
- для всякого простого
получаем
Нахождение порядка мультипликативной группы кольца вычетов
правитьМультипликативная группа кольца вычетов по модулю состоит из классов вычетов[41].
Пример. Приведённая система вычетов по модулю 14 состоит из классов вычетов:
Приложения в теории групп
правитьЧисло порождающих элементов в конечной циклической группе равно . В частности, если мультипликативная группа кольца вычетов по модулю является циклической группой — что возможно только при , где — простое нечётное, — натуральное[42], — то существует генераторов группы (первообразных корней по модулю ).
Пример. Группа рассмотренная в примере выше, имеет генератора: и
Нерешенные вопросы
правитьЗадача Лемера
правитьКак известно, если — простое, то В 1932 году Деррик Лемер[англ.] задался вопросом, существует ли такое составное число , что является делителем . Лемер рассматривал уравнение:
где — целое. Ему удалось доказать, что если — решение уравнения, то либо — простое, либо оно является произведением семи или более различных простых чисел[43]. Позже были доказаны и другие сильные утверждения. Так, в 1980 году Cohen и Hagis показали, что если составное и делит то и где — количество простых делителей. В 1970 году Lieuwens установил, что если то и Wall в 1980 году доказал, что если то [44].
По сей день неизвестно, существуют ли составные решения задачи Лемера. Если предположить, что их не существует, то получается следующий критерий простоты: — простое тогда и только тогда, когда [43].
Гипотеза Кармайкла
правитьЕсли посмотреть даже на первые десять значений функции Эйлера {1, 1, 2, 2, 4, 2, 6, 4, 6, 4}, бросается в глаза, что среди них много повторяющихся. Гипотеза Кармайкла состоит в том, что нет такого значения , которое функция Эйлера принимала бы только один раз.
В 1907 году Кармайкл предложил как упражнение доказать следующее утверждение[45]:
- Если — натуральное число, то существует натуральное число такое, что
Иначе это утверждение можно сформулировать так[46]: не существует натурального числа такого, что
Однако в 1922 году Кармайкл обнаружил, что предложенное им доказательство содержит ошибку. В этом же году он показал, что если то Позже эта оценка неоднократно улучшалась, и современное значение нижней границы, с которой стоит начинать искать контрпример для гипотезы Кармайкла, есть Это значение получили Schlafly и Wagon в 1994 году, используя метод Klee[45].
В 1999 году Форд доказал следующую теорему[47]:
Это означает, что, задавшись некоторым числом можно найти среди множества значений функции Эйлера такое значение что оно принимается ровно раз. Однако, доказать, что нет такого значения, которое функция Эйлера принимала бы только один раз, до сих пор никому не удалось[46].
См. также
правитьПримечания
править- ↑ Эйлера функция // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5. — С. 934.
- ↑ Sandifer, 2007, p. 203.
- ↑ Габидулин, 2011, Системы RSA.
- ↑ последовательность A000010 в OEIS
- ↑ Burton, 2007, Theorem 7.2, p. 133.
- ↑ Hardy, 1975, Theorem 59, p. 52.
- ↑ Hardy, 1975, Theorem 60, p. 53.
- ↑ Перейти обратно: 1 2 3 Сагалович, 2007, Вычисление функции Эйлера, p. 35—36.
- ↑ Burton, 2007, Euler's Phi-Function, p. 136.
- ↑ Weisstein, MathWorld, Totient Function
- ↑ Ruiz, S., A Congruence With the Euler Totient Function, 2004
- ↑ Виноградов, 1952, Функция Эйлера.
- ↑ Информация в этом разделе основана на статье: Coleman, Some remarks on Euler’s totient function
- ↑ Gupta H., 1981
- ↑ Перейти обратно: 1 2 3 Handbook, 2005, Elementary inequalities for φ.
- ↑ Kendall and Osborn 1965
- ↑ Sierpiński and Schinzel 1988
- ↑ Hardy, 1975, Theorem 326, p. 267.
- ↑ Hardy, 1975, Theorem 327, p. 267.
- ↑ Перейти обратно: 1 2 3 Ribenboim, 1996, Values of Euler's Function, p. 38.
- ↑ Hardy, 1975, Theorem 330, p. 268.
- ↑ Hardy, 1975, Theorem 332, p. 269.
- ↑ Hardy, 1975, Theorem 329, p. 267.
- ↑ Handbook, 2005, On the function n/φ(n).
- ↑ Hardy, 1975, Theorem 328, p. 267.
- ↑ Rosser, J. Barkley and Schoenfeld, Lowell. Approximate formulas for some functions of prime numbers (англ.) // Illinois J. Math. : journal. — 1962. — Vol. 6, no. 1. — P. 64—94. (Theorem 15)
- ↑ Перейти обратно: 1 2 Ribenboim, 1996, Distribution of Values of Euler's Function, p. 320.
- ↑ Nicolas, 1983
- ↑ Виноградов, 1952, с. 29—31.
- ↑ Rosica Dineva, The Euler Totient, the Möbius, and the Divisor Functions
- ↑ Hardy, 1975, Theorem 288, p. 250.
- ↑ Hardy, 1975, Theorem 309, p. 258.
- ↑ Schramm, 2008
- ↑ Ватутин Э.И. О перечислении циклических латинских квадратов и расчете значения функции Эйлера с их использованием // Высокопроизводительные вычислительные системы и технологии. 2020. Т. 4, № 2. С. 40–48.
- ↑ Габидулин, 2011, Система шифрования RSA, с. 96.
- ↑ Алфёров, 2002, p. 462—463.
- ↑ Перейти обратно: 1 2 Schneier, 1995, The Euler Totient Function.
- ↑ Габидулин, 2011, Нахождение мультипликативного обратного по модулю, с. 233.
- ↑ Schneier, 1995, Number Theory.
- ↑ Сагалович, 2007, с. 36.
- ↑ Сагалович, 2007, Приведенная система вычетов.
- ↑ Виноградов, 1952, с. 106.
- ↑ Перейти обратно: 1 2 Lehmer, 1932
- ↑ Ribenboim, 1996, p. 36—37.
- ↑ Перейти обратно: 1 2 Ribenboim, 1996, p. 39—40.
- ↑ Перейти обратно: 1 2 Coleman, Some remarks on Euler’s totient function
- ↑ Ford, 1999
Литература
править- Charles Sandifer. The early mathematics of Leonhard Euler. — MAA, 2007. — С. 391. — ISBN 0-88385-559-3.
- József Sándor, Dragoslav S. Mitrinovic, Borislav Crstici. Euler's φ-function // Handbook of Number Theory I. — Springer, 2005. — 622 с.
- Виноградов И. М. Основы теории чисел. — 5-е изд. — М.—Л.: Гостехиздат, 1952. — 180 с. — 100 000 экз.
- G. H. Hardy, E. M. Wright. An Introduction to the Theory of Numbers. — fourth edition. — Oxford: Oxford University Press, 1975. — 421 с.
- Алферов А. П., Зубов А. Ю., Кузьмин А. С., Черемушкин А. В. Элементы алгебры и теории чисел // Основы криптографии. — 2-е изд., испр. и доп. — М.: Гелиос АРВ, 2002. — 480 с. — ISBN 5-85438-025-0.
- Bruce Schneier. Applied Cryptography: Protocols, Algorithms and Source Code in C. — Australia: John Wiley & Sons, 1995. — ISBN 0-471-12845-7.
- Сагалович Ю. Л. Введение в алгебраические коды — М.: МФТИ, 2007. — 262 с. — ISBN 978-5-7417-0191-1
- Paulo Ribenboim. The New Book of Prime Number Records. — New York: Springer, 1996. — ISBN 0-387-94457-5.
- Габидулин Э. М., Кшевецкий А. С., Колыбельников А. И. Защита информации: учебное пособие. — М.: МФТИ, 2011. — 262 с. — ISBN 5-7417-0377-9.
- David M. Burton. Elementary Number Theory. — Sixth Edition. — University of New Hampshire: McGraw-Hill, 2007. — 512 с. — ISBN 978-0-07-305188-8.
- Арнольд В. И. Группы Эйлера и арифметика геометрических прогрессий. — М.: МЦНМО, 2003. — 44 с. — ISBN 5-94057-141-7.
Ссылки
править- Арнольд В. И., Группы Эйлера и арифметика геометрических прогрессий (2003)
- Coleman R., Some remarks on Euler’s totient function (2012)
- Dineva R., The Euler Totient, the Möbius, and the Divisor Functions (2005)
- Ford K., The number of solutions of φ(x) = m (1999)
- József Sándor, Dragoslav S. Mitrinovic, Borislav Crstici, Handbook of Number Theory I (2005)
- Gupta H., Euler’s totient function and its inverse (1981)
- Hardy, Wright An Introduction to the Theory of Numbers (2008)
- Lehmer D. H., On Euler’s Totient Function (1932)
- Ruiz S., A Congruence With the Euler Totient Function (2004)
- Schramm, Wolfgang, The Fourier Transform of Functions of the Greatest Common Divisor (2008)
- Weisstein, Eric W. «Totient Function.» From MathWorld — A Wolfram Web Resource. http://mathworld.wolfram.com/TotientFunction.html
Для улучшения этой статьи желательно:
|


