Внешнепланарный граф

Внешнепланарный граф — в теории графов такой граф, который допускает планарную диаграмму, в которой все вершины принадлежат внешней грани.

Максимальный внешнепланарный граф и его 3-раскраска.

Полный граф K₄ является наименьшим планарным графом, не являющимся внешнепланарным.

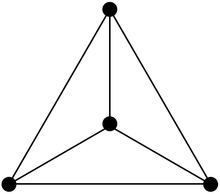
Внешнепланарные графы можно охарактеризовать (аналогично теореме Вагнера для планарных графов) двумя запрещёнными минорами K₄и K_2,3, или их инвариантами Колен де Вердьера. Эти графы имеют гамильтоновы циклы тогда и только тогда, когда они двусвязны, и в этом случае внешняя грань образует единственный гамильтонов цикл. Любой внешнепланарный граф раскрашиваем в 3 цвета и имеет вырожденность и древесную ширину не больше 2.

Внешнепланарные графы являются подмножеством планарных графов, подграфами параллельно-последовательных графов и круговых графов. Максимальный внешнепланарный граф — это граф, к которому нельзя добавить ребро без потери внешнепланарности. Они также являются хордальными и графами видимости.

История

Внешнепланарные графы впервые изучали и назвали Шартран и Харари при рассмотрении задачи определения планарности графов, образованных при помощи совершенных паросочетаний, связывающих две копии базового графа (например, многие из обобщённых графов Петерсена образованы этим способом из двух копий графа-цикла). Как они показали, если базовый граф двусвязен, граф, полученный из него описанным способом, планарен тогда и только тогда, когда базовый граф внешнепланарен и паросочетание образует диэдральные перестановки внешнего цикла.

Определение и описание

Внешнепланарный граф является неориентированным графом, который можно нарисовать на плоскости без пересечений таким образом, что все вершины принадлежат внешней неограниченной грани рисунка. То есть никакая из вершин не окружена полностью рёбрами. Альтернативно граф G внешнепланарен, если граф, образованный из G добавлением новой вершины, соединённой рёбрами со всеми остальными вершинами, планарен.

Максимальный внешнепланарный граф — это внешнепланарный граф, к которому нельзя добавить какое-либо ребро, не нарушив свойство внешнепланарности. Любой максимальный внешнепланарный граф с n вершинами имеет в точности 2n − 3 рёбер и любая ограниченная грань максимального внешнепланарного графа является треугольником.

Запрещённые графы

Внешнепланарные графы имеют характеризацию запрещёнными графами, аналогичную теореме Понтрягина — Куратовского и теореме Вагнера для планарных графов — граф внешнепланарен тогда и только тогда, когда он не содержит подразбиения полного графа K₄ или полного двудольного графа K_2,3 . Альтернативно, граф внешнепланарен тогда и только тогда, когда он не содержит K₄ или K_2,3 в качестве минора, графа, полученного путём удаления и стягивания рёбер.

Граф без треугольников внешнепланарен тогда и только тогда, когда он не содержит подразделений K_2,3.

Инвариант Колина де Вердьера

Граф внешнепланарен тогда и только тогда, когда его инвариант Колен де Вердьера не превосходит двух. Графы, характеризующиеся подобным образом по значению инварианта Колен де Вердьера (не превосходящего значение 1, 3 или 4) — это линейные леса, планарные графы и вложимые без зацепления графы.

Свойства

Двусвязность и гамильтоновость

Внешнепланарный граф является двусвязным тогда и только тогда, когда внешняя грань образует простой цикл без повторения вершин. Внешнепланарный граф является гамильтоновым тогда и только тогда, когда он двусвязен. В этом случае внешняя грань образует единственный гамильтонов цикл. Более обще, размер наиболее длинного цикла во внешнепланарном графе равен числу вершин в наибольшей двусвязной компоненте. По этой причине поиск гамильтоновых циклов и наиболее длинных циклов во внешнепланарных графах может быть осуществлён за линейное время, в контраст к NP-полноте этих задач для произвольных графов.

Любой максимальный внешнепланарный граф удовлетворяет более сильным условиям, чем гамильтоновость — он вершинно панцикличен, что означает, что для любой вершины v и любого числа k в интервале от трёх до числа вершин графа существует цикл длины k, содержащий v. Цикл такой длины может быть найден последовательным удалением треугольника, соединённого с остатком графа единственным ребром, таких, что удаляемая вершина не совпадает с v, пока внешняя грань оставшегося графа не станет длины k.

Планарный граф является внешнепланарным тогда и только тогда, когда все его двусвязные компоненты внешнепланарны.

Раскраска

Все внешнепланарные графы без петель могут быть раскрашены всего тремя цветами. Этот факт проявляется заметно в упрощенном доказательстве теоремы о картинной галерее Хватала Фиском. Раскраска тремя цветами может быть найдена за линейное время алгоритмом жадной раскраски, который удаляет любую вершину со степенью, не превосходящей двух и раскрашивает оставшийся граф рекурсивно, а затем возвращает каждую из удалённых вершин с цветом, отличным от цветов двух её соседей.

Согласно теореме Визинга хроматический индекс любого графа (минимальное число цветов, необходимых для раскраски рёбер графа так, что никакие два смежных ребра не имеют один цвет) либо равен максимуму степеней вершин графа, либо на единицу больше максимальной степени. Для внешнепланарных графов хроматический индекс равен максимальной степени, если только граф не является циклом нечётной длины. Рёберная раскраска с оптимальным числом цветов может быть найдена за линейное время на основе поиска в ширину слабого двойственного дерева.

Другие свойства

Внешнепланарные графы имеют вырожденность, не превосходящую 2 — любой подграф внешнепланарного графа содержит вершину со степенью, не превосходящей 2.

Внешнепланарные графы имеют древесную ширину, не превосходящую 2, откуда следует, что много задач оптимизации на графах, которые NP-полны для графов общего вида, могут быть решены за полиномиальное время с помощью динамического программирования, если входом служит внешнепланарный граф. Более обще, k-внешнепланарный граф имеет древесную ширину O(k).

Любой внешнепланарный граф можно представить в виде графа пересечений прямоугольников с параллельными осям сторонами, так что внешнепланарные графы имеют интервальную размерность максимум два.

Связанные семейства графов

Кактус. Кактусы образуют подкласс внешнепланарных графов.

Любой внешнепланарный граф является планарным. Любой внешнепланарный граф является подграфом параллельно-последовательного графа. Однако не все параллельно-последовательные графы внешнепланарны. Полный двудольный граф K_2,3 является планарным и параллельно-последовательным, но не внешнепланарным. С другой стороны, полный граф K₄ планарен, но ни параллельно-последователен, ни внешнепланарен. Любой лес и любой кактус внешнепланарны.

Cлабо двойственный планарный граф вложенного внешнепланарного графа (граф, имеющий по вершине для каждой ограниченной грани вложения и по ребру для смежных ограниченных граней) является лесом, а слабо двойственный планарный граф графа Халина является внешнепланарным графом. Планарный граф является внешнепланарным тогда и только тогда, когда его слабо двойственный является лесом, и граф является графом Халина тогда и только тогда, когда его слабо двойственный является двусвязным и внешнепланарным.

Существует понятие степени внешнепланарности. 1-внешнепланарное вложение графа — это то же самое, что внешнепланарное вложение. Для k > 1 говорят, что планарное вложение является k-внешнепланарным, если удаление вершины из внешней грани приводит к (k − 1)-внешнепланарному вложению. Граф является k-внешнепланарным тогда и только тогда, когда он имеет k-внешнепланарное вложение.

Любой максимальный внешнепланарный граф является хордальным графом. Любой максимальный внешнепланарный граф является графом видимости простого многоугольника. Максимальные внешнепланарные графы образуются как графы триангуляции многоугольников. Они являются также примерами 2-деревьев, параллельно-последовательноых графов и хордальных графов.

Любой внешнепланарный граф является круговым графом, графом пересечений множества хорд окружности.

Ссылки

• Outerplanar graphs, Information System on Graph Classes and Their Inclusions
• Weisstein, Eric W. Outplanar Graph (англ.) на сайте Wolfram MathWorld.