В теории графов графом Халина называется некоторый вид планарного графа, который строится из дерева, имеющего по меньшей мере 4 вершины, ни одна из которых не имеет в точности двух соседей. Дерево рисуется на плоскости так, что никакие рёбра не пересекаются, затем добавляются рёбра, соединяющие все его листья в цикл[1]. Графы Халина названы по имени немецкого математика Рудольфа Халина[англ.], изучавшего их в 1971 году[2], но кубические графы Халина изучались за столетие до этого английским математиком Томасом Киркманом[англ.][3].
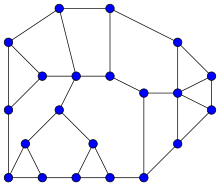
Построение
правитьГраф Халина строится следующим образом: пусть — вложенное в плоскость дерево с четырьмя или более вершинами, такой, что никакая вершина графа не имеет степень два (то есть, никакая вершина не имеет в точности двух соседей). Граф Халина создаётся путём добавления к графу цикла, проходящего через все листья таким образом, что расширяющий путь остаётся планарным.
Примеры
правитьЗвезда — это дерево с единственной внутренней вершиной. Применяя построение Халина получим колесо, граф пирамиды. Граф треугольной призмы является также графом Халина — его можно нарисовать так, что одна из его прямоугольных граней будет внешним циклом, а оставшиеся рёбра образуют дерево с четырьмя листьями, двумя внутренними вершинами и пятью рёбрами.
Граф Фрухта, один из двух наименьших кубических графов с нетривиальными автоморфизмами, является также графом Халина.
Свойства
правитьЛюбой граф Халина 3-связен, что означает, что нельзя разбить граф на два графа путём удаления двух вершин. Он также рёберно минимально 3-связен, что означает, что после удаления любого ребра граф перестаёт быть 3-связен[1]. По теореме Штайница, будучи 3-связным планарным графом, граф Халина можно представить в виде множества вершин и рёбер выпуклого многогранника. Таким образом, он является графом многогранника, но в этом случае, как и для любого графа многогранника, его вложение в плоскость единственно с точностью до выбора грани, которая будет его внешней гранью[1].
Любой граф Халина является гамильтоновым графом и любое ребро принадлежит гамильтонову циклу. Более того, любой граф Халина остаётся гамильтоновым после удаления любой вершины [4]. Поскольку любое дерево без вершин степени 2 содержит два листа с одним родителем, любой граф Халина содержит треугольник. В частности, граф Халина не может быть ни графом без треугольников, ни двудольным графом. Более строго, любой граф Халина является почти панциклическим, в том смысле, что он имеет циклы всех длин от 3 до n с возможным исключением одной чётной длины. Более того, любой граф Халина остаётся почти панциклическим после стягивания одного ребра, и любой граф Халина без внутренних вершин степени три является панциклическим [5].
Любой граф Халина имеет древесную ширину максимум три [6]. Таким образом, многие задачи оптимизации, являющиеся NP-полными для произвольных графов, такие как нахождение независимого множества, для графов Халина можно решить за линейное время при использовании динамического программирования[7].
Слабый двойственный граф вложенного планарного графа имеет вершины, соответствующие граням планарного графа и рёбра, соответствующие смежным граням (слабый двойственный получается из двойственного путём удаления вершины, соответствующей внешней грани). Слабый двойственный граф графа Халина всегда двусвязен и внешнепланарен. Это свойство можно использовать для характеризации графов Халина — вложенный в плоскость планарный граф является графом Халина с циклом через листья как внешней грани вложения тогда и только тогда, когда его слабый двойственный двусвязен и внешнепланарен[8].
История
правитьВ 1971 году Халин (Halin) предложил графы (получившие название графов Халина) как класс минимальных 3-вершинно-связных графов — для каждого ребра графа его удаление уменьшает связность[2]. Эти графы приобрели особое значение, когда выяснилось, что многие алгоритмические задачи, решение которых нереально для произвольных планарных графов, могут быть решены эффективно на графах Халина[4][8], что впоследствии объяснено как следствие их малой ширины дерева[6][7].
До работ Халина задачей перечисления кубических графов Халина занимался в 1856 году Томас Киркман[англ.][3], а в 1965 году — Ганс Радемахер[9] называл эти графы основанными на многогранниках. Он определил их как кубические графы многогранников с f гранями, у которых одна из граней имеет f − 1 рёбер. Графы, удовлетворяющие этому определению — в точности кубические графы Халина.
Графы Халина также иногда называют многогранниками без крыши[4] но, как и название «основанные на многранниках» это название можно отнести к кубическим графам Халина[10]. Выпуклые многогранники, графами которых являются графы Халина, называют также куполами[11].
Примечания
править- ↑ 1 2 3 Encyclopaedia of Mathematics, first Supplementary volume, 1988, ISBN 0-7923-4709-9, p. 281, статья «Halin Graph» Архивная копия от 11 января 2014 на Wayback Machine
- ↑ 1 2 Halin. Combinatorial Mathematics and its Applications (Proc. Conf., Oxford, 1969). — London: Academic Press, 1971. — С. 129—136.
- ↑ 1 2 Th. P. Kirkman (1856), "On the enumeration of x-edra having triedral summits and an (x − 1)-gonal base", Philosophical Transactions of the Royal Society of London, pp. 399–411, JSTOR 108592
- ↑ 1 2 3 G. Cornuéjols, D. Naddef, W. R. Pulleyblank (1983), Halin graphs and the travelling salesman problem, vol. 26, pp. 287–294, doi:10.1007/BF02591867
{{citation}}: Неизвестный параметр|выпуск=игнорируется (справка); Неизвестный параметр|издание l=игнорируется (справка)Википедия:Обслуживание CS1 (множественные имена: authors list) (ссылка) - ↑ Skowrońska. Cycles in Graphs. — Elsevier Science Publishers B.V., 1985. — Т. 27. — С. 179—194. — (Annals of Discrete Mathematics).
- ↑ 1 2 Hans Bodlaender. Planar graphs with bounded treewidth. — Department of Computer Science, Utrecht University, 1988. — (Technical Report RUU-CS-88-14). Архивировано 28 июля 2004 года.
- ↑ 1 2 Hans Bodlaender. Proceedings of the 15th International Colloquium on Automata, Languages and Programming. — Springer—Verlag, 1988. — Т. 317. — С. 105—118. — (Lecture Notes in Computer Science).
- ↑ 1 2 Maciej M. Sysło, Andrzej Proskurowski. Graph Theory: Proceedings of a Conference held in Lagów, Poland, February 10—13, 1981. — Springer—Verlag, 1983. — Т. 1018. — С. 248—256. — (Lecture Notes in Mathematics). — doi:10.1007/BFb0071635.
- ↑ Hans Rademacher. On the number of certain types of polyhedra // Illinois Journal of Mathematics. — 1965. — Т. 9. — С. 361—380.
- ↑ L. Lovász, M. D. Plummer. Combinatorics (Proc. British Combinatorial Conf., Univ. Coll. Wales, Aberystwyth, 1973). — London: Cambridge Univ. Press, 1974. — С. 103—107. London Math. Soc. Lecture Note Ser., No. 13.
- ↑ Erik D. Demaine, Martin L. Demaine, Ryuhei Uehara. Proceedings of the 25th Canadian Conference on Computational Geometry (CCCG 2013), Waterloo, Ontario, Canada, August 8–10, 2013. — 2013. — С. 43—48. Архивировано 24 июля 2018 года.
Ссылки
править- Halin graphs, Information System on Graph Class Inclusions.
- Weisstein, Eric W. Halin Graph (англ.) на сайте Wolfram MathWorld.
Для улучшения этой статьи желательно:
|