Полиэдральный граф
Полиэдральный граф — неориентированный граф, образованный из вершин и рёбер выпуклого многогранника, или, в контексте теории графов — вершинно 3-связный планарный граф.
Описание
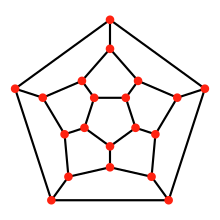
правитьДиаграмма Шлегеля выпуклого многогранника представляет его вершины и рёбра как точки и отрезки на евклидовой плоскости, образуя разбиение внешнего выпуклого многоугольника на более мелкие выпуклые многоугольники. Диаграмма не имеет самопересечений, так что любой полиэдральный граф является также планарным. Кроме того, по теореме Балинского, этот граф является вершинно 3-связным.
Согласно теореме Штейница этих двух свойств достаточно, чтобы полностью описать полиэдральные графы — это в точности вершинно 3-связные планарные графы. Таким образом, если граф и планарен, и вершинно 3-связен, существует многогранник, вершины и рёбра которого образуют изоморфный исходному граф[1][2]. Если задан такой граф, представление его в виде разбиения выпуклого многоугольника на меньшие выпуклые многоугольники может быть найдено с помощью вложение Татта[3].
Гамильтоновость и показатель короткости
правитьТэйт высказал гипотезу, что любой кубический полиэдральный граф (то есть полиэдральный граф, в котором каждая вершина инцидентна в точности трём рёбрам) имеет гамильтонов цикл, но эта гипотеза была опровергнута Уильямом Таттом, построившим контрпример — полиэдральный негамильтонов граф (граф Татта). Если ослабить условие, что граф должен быть кубическим, появится много других меньших по размерам негамильтоновых полиэдральных графов, один из них, имеющий 11 вершин и 18 рёбер — граф Хершеля[4], существует также негамильтонов полиэдральный граф с 11 вершинами, в котором все грани треугольны — граф Голднера — Харари[5].
Строго говоря, существует константа (показатель короткости[уточнить]) и бесконечное семейство полиэдральных графов, таких что длина самого длинного простого пути графа с вершинами в семействе равна [6][7].
Комбинаторное перечисление
правитьВ 1996 году определено число полиэдральных графов, имеющих до 26 рёбер[8], в частности, число таких графов с 6, 7, …, 21 рёбрами равно:
- 1, 0, 1, 2, 2, 4, 12, 22, 58, 158, 448, 1342, 4199, 13384, 43708, 144810[9].
Можно также перечислить полиэдральные графы по числу их вершин, число таких графов равно:
- 1, 2, 7, 34, 257, 2606, 32300, 440564, 6384634, 96262938, 1496225352, …[10].
Специальные случаи
правитьПолиэдральный граф — граф простого многогранника, если он является кубическим (в каждую вершину сходятся три ребра), и это граф симплициального многогранника, если он является максимальным планарным графом. Графы Халина, образованные из планарных деревьев путём добавления внешнего цикла, проходящего через все листья дерева, образуют другой важный подкласс полиэдральных графов.
Примечания
править- ↑ Günter M. Ziegler. Lectures on Polytopes. — 1995. — С. 103, Глава 4 "Steinitz' Theorem for 3-Polytopes". — ISBN 0-387-94365-X.
- ↑ Branko Grünbaum. Convex Polytopes. — Springer-Verlag, 2003. — Т. 221. — (Graduate Texts in Mathematics). — ISBN 978-0-387-40409-7.
- ↑ W. T. Tutte. How to draw a graph // Proceedings of the London Mathematical Society. — 1963. — Т. 13. — С. 743–767. — doi:10.1112/plms/s3-13.1.743.
- ↑ Weisstein, Eric W. Herschel Graph (англ.) на сайте Wolfram MathWorld.
- ↑ Weisstein, Eric W. Goldner-Harary Graph (англ.) на сайте Wolfram MathWorld.
- ↑ Weisstein, Eric W. Shortness Exponent (англ.) на сайте Wolfram MathWorld.
- ↑ Branko Grünbaum, T. S. Motzkin. Longest simple paths in polyhedral graphs // Journal of the London Mathematical Society. — 1962. — Т. s1-37, вып. 1. — С. 152–160. — doi:10.1112/jlms/s1-37.1.152.
- ↑ A. J. W. Duijvestijn. The number of polyhedral (3-connected planar) graphs // Mathematics of Computation. — 1996. — Т. 65. — С. 1289–1293. — doi:10.1090/S0025-5718-96-00749-1. Архивировано 17 февраля 2019 года.
- ↑ последовательность A002840 в OEIS
- ↑ последовательность A000944 в OEIS
Ссылки
править- Weisstein, Eric W. Polyhedral Graph (англ.) на сайте Wolfram MathWorld.
Для улучшения этой статьи желательно:
|