Дзета-функция Римана

Запрос «Дзета-функция» перенаправляется сюда; см. также другие значения.

Для термина «Функция Римана» см. также другие значения.

Дзе́та-фу́нкция Ри́мана — функция $\displaystyle \zeta (s)$ комплексного переменного $s=\sigma +it$, при $\sigma >1$, определяемая с помощью ряда Дирихле:

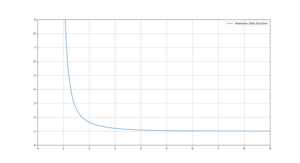
График дзета-функции Римана (аналитического продолжения ряда Дирихле) на действительной оси. Слева от нуля масштаб шкалы значений функции увеличен в 100 раз для наглядности

$\zeta (s)={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\ldots .$

В комплексной полуплоскости $\{s\in \mathbb {C} \mid \operatorname {Re} s>1\}$ этот ряд сходится, является аналитической функцией от $s$ и допускает аналитическое продолжение на всю комплексную плоскость, за исключением особой точки $s=1$.

Дзета-функция Римана играет очень важную роль в аналитической теории чисел, имеет приложения в теоретической физике, статистике, теории вероятностей.

В частности, если будет доказана или опровергнута до сих пор ни доказанная, ни опровергнутая гипотеза Римана о положении всех нетривиальных нулей дзета-функции на прямой комплексной плоскости $\operatorname {Re} s=1/2$, то многие важные теоремы о простых числах, опирающиеся в доказательстве на гипотезу Римана, станут либо истинными, либо ложными.

Дзета-функция Римана для вещественных s > 1

Тождество Эйлера

В области $\{s\mid \operatorname {Re} s>1\}$ также верно представление в виде бесконечного произведения (тождество Эйлера)

$\zeta (s)=\prod _{{\text{число }}p \atop {\text{простое}}}{\frac {1}{1-p^{-s}}}.$

Доказательство

Решето Эратосфена для поиска простых чисел используется в этом доказательстве

Идея доказательства использует лишь простую алгебру, доступную прилежному школьнику. Изначально этим способом Эйлер вывел формулу. Есть свойство решета Эратосфена, из которого мы можем извлечь пользу:

$\zeta (s)=1+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+{\frac {1}{4^{s}}}+{\frac {1}{5^{s}}}+\ldots$

${\frac {1}{2^{s}}}\zeta (s)={\frac {1}{2^{s}}}+{\frac {1}{4^{s}}}+{\frac {1}{6^{s}}}+{\frac {1}{8^{s}}}+{\frac {1}{10^{s}}}+\ldots$

Вычитая второе из первого, мы удаляем все элементы с делителем 2:

$\left(1-{\frac {1}{2^{s}}}\right)\zeta (s)=1+{\frac {1}{3^{s}}}+{\frac {1}{5^{s}}}+{\frac {1}{7^{s}}}+{\frac {1}{9^{s}}}+{\frac {1}{11^{s}}}+{\frac {1}{13^{s}}}+\ldots$

Повторяем для следующего:

${\frac {1}{3^{s}}}\left(1-{\frac {1}{2^{s}}}\right)\zeta (s)={\frac {1}{3^{s}}}+{\frac {1}{9^{s}}}+{\frac {1}{15^{s}}}+{\frac {1}{21^{s}}}+{\frac {1}{27^{s}}}+{\frac {1}{33^{s}}}+\ldots$

Опять вычитаем, получаем:

$\left(1-{\frac {1}{3^{s}}}\right)\left(1-{\frac {1}{2^{s}}}\right)\zeta (s)=1+{\frac {1}{5^{s}}}+{\frac {1}{7^{s}}}+{\frac {1}{11^{s}}}+{\frac {1}{13^{s}}}+{\frac {1}{17^{s}}}+\ldots ,$

где удалены все элементы с делителями 2 и/или 3.

Как можно увидеть, правая сторона просеивается через решето. Бесконечно повторяя, получаем:

$\ldots \left(1-{\frac {1}{11^{s}}}\right)\left(1-{\frac {1}{7^{s}}}\right)\left(1-{\frac {1}{5^{s}}}\right)\left(1-{\frac {1}{3^{s}}}\right)\left(1-{\frac {1}{2^{s}}}\right)\zeta (s)=1.$

Поделим обе стороны на всё, кроме $\zeta (s)$, получим:

$\zeta (s)={\frac {1}{\left(1-{\dfrac {1}{2^{s}}}\right)\left(1-{\dfrac {1}{3^{s}}}\right)\left(1-{\dfrac {1}{5^{s}}}\right)\left(1-{\dfrac {1}{7^{s}}}\right)\left(1-{\dfrac {1}{11^{s}}}\right)\ldots }},$

что можно записать короче как бесконечное произведение по всем простым p:

$\zeta (s)=\prod _{p}{\frac {1}{1-p^{-s}}}.$

Чтобы сделать доказательство строгим, необходимо потребовать только лишь, чтобы, когда $\operatorname {Re} s>1$, просеиваемая правая часть приближалась к 1, что немедленно следует из сходимости ряда Дирихле для $\zeta (s)$.

Это равенство представляет собой одно из основных свойств дзета-функции.

Свойства

Дзета-функции Римана в комплексной плоскости

• Если взять асимптотическое разложение при ${N\rightarrow +\infty }$ частичных сумм вида

  $\sum \limits _{n=1}^{N}{\frac {1}{n^{s}}}=\zeta (s)+{\frac {1}{1-s}}N^{1-s}+{\frac {1}{2}}N^{-s}-{\frac {1}{12}}sN^{-1-s}+\dots$,

справедливую для ${\rm {Re}}\,s>1$, она же останется верной и для всех $s$, кроме тех, для которых $2-s\in {\mathbb {N} }$ (это тривиальные корни дзета-функции). Из этого можно получить следующие формулы для $\zeta (s)$:

1. $\zeta (s)=\lim \limits _{N\rightarrow +\infty }\left(\sum \limits _{n=1}^{N}{\frac {1}{n^{s}}}-{\frac {N^{1-s}}{1-s}}\right)$, при ${\rm {Re}}\,s>0$, кроме $s=1$;
2. $\zeta (s)=\lim \limits _{N\rightarrow +\infty }\left(\sum \limits _{n=1}^{N}{\frac {1}{n^{s}}}-{\frac {N^{1-s}}{1-s}}-{\frac {1}{2}}N^{-s}\right)$, при ${\rm {Re}}\,s>-1$, кроме $s=1$ или $0$;
3. $\zeta (s)=\lim \limits _{N\rightarrow +\infty }\left(\sum \limits _{n=1}^{N}{\frac {1}{n^{s}}}-{\frac {N^{1-s}}{1-s}}-{\frac {1}{2}}N^{-s}+{\frac {1}{12}}sN^{-1-s}\right)$, при ${\rm {Re}}\,s>-2$, кроме $s=1$, $0$ или $-1$ и т. д.

• Существуют явные формулы для значений дзета-функции в чётных целых точках:

  $\zeta (2m)=(-1)^{m+1}{\frac {(2\pi )^{2m}}{2(2m)!}}B_{2m}$, где $\displaystyle B_{2m}$ — число Бернулли.

В частности, $\zeta (2)={\frac {\pi ^{2}}{6}}$ (ряд обратных квадратов), $\zeta (4)={\frac {\pi ^{4}}{90}},\ \ \zeta (6)={\frac {\pi ^{6}}{945}},\ \ \zeta (8)={\frac {\pi ^{8}}{9450}},\ \ \zeta (10)={\frac {\pi ^{10}}{93555}}$

• Кроме того, получено значение $\zeta (3)=-{\frac {\psi ^{(2)}(1)}{2}}$, где $\psi$ — полигамма-функция;
• Про значения дзета-функции в нечётных целых точках известно мало: предполагается, что они являются иррациональными и даже трансцендентными, но пока (2019 г.) доказана только лишь иррациональность числа ζ(3) (Роже Апери, 1978), а также то, что среди значений ζ(5), ζ(7), ζ(9), ζ(11) есть хотя бы ещё одно иррациональное.
• При $\operatorname {Re} \,s>1$
  • ${\frac {1}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n^{s}}}$, где $\displaystyle \mu (n)$ — функция Мёбиуса
  • ${\frac {\zeta (2s)}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {\lambda (n)}{n^{s}}}$, где $\displaystyle \lambda (n)$ — функция Лиувилля
  • $\zeta ^{2}(s)=\sum _{n=1}^{\infty }{\frac {\tau (n)}{n^{s}}}$, где $\displaystyle \tau (n)$ — число делителей числа $\displaystyle n$
  • ${\frac {\zeta (s)}{\zeta (2s)}}=\sum _{n=1}^{\infty }{\frac {|\mu (n)|}{n^{s}}}$
  • ${\frac {\zeta ^{2}(s)}{\zeta (2s)}}=\sum _{n=1}^{\infty }{\frac {2^{\nu (n)}}{n^{s}}}$, где $\displaystyle \nu (n)$ — число простых делителей числа $\displaystyle n$
  • ${\frac {\zeta ^{3}(s)}{\zeta (2s)}}=\sum _{n=1}^{\infty }{\frac {\tau (n^{2})}{n^{s}}}$
  • ${\frac {\zeta ^{4}(s)}{\zeta (2s)}}=\sum _{n=1}^{\infty }{\frac {(\tau (n))^{2}}{n^{s}}}$
• При $\operatorname {Re} \,s>2$
  • ${\frac {\zeta (s-1)}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {\varphi (n)}{n^{s}}}$, где $\displaystyle \varphi (n)$ — функция Эйлера
• $\displaystyle \zeta (s)$ имеет в точке $\displaystyle s=1$ простой полюс с вычетом, равным 1.
• Дзета-функция при $\displaystyle s\neq 0,s\neq 1$ удовлетворяет уравнению:

  $\zeta (s)=2^{s}\pi ^{s-1}\sin \left({\pi s \over 2}\right)\Gamma (1-s)\zeta (1-s)$,

где $\displaystyle \Gamma (z)$ — гамма-функция Эйлера. Это уравнение называется функциональным уравнением Римана, хотя последний и не является ни его автором, ни тем, кто его первым строго доказал.

• Для функции

  $\xi (s)={\frac {1}{2}}\pi ^{-s/2}s(s-1)\Gamma \left({\frac {s}{2}}\right)\zeta (s)$,

введённой Риманом для исследования $\displaystyle \zeta (s)$ и называемой кси-функцией Римана, это уравнение принимает вид:

$\displaystyle \ \xi (s)=\xi (1-s)$.

Нули дзета-функции

Основная статья: Гипотеза Римана

Как следует из функционального уравнения Римана, в полуплоскости $\operatorname {Re} \,s<0$ функция $\zeta (s)$ имеет лишь простые нули в отрицательных чётных точках: $0=\zeta (-2)=\zeta (-4)=\zeta (-6)=\dots$. Эти нули называются «тривиальными» нулями дзета-функции. Далее, $\zeta (s)\neq 0$ при вещественных $s\in (0,1)$. Следовательно, все «нетривиальные» нули дзета-функции являются комплексными числами. Кроме того, они обладают свойством симметрии относительно вещественной оси и относительно вертикали $\operatorname {Re} \,s={\frac {1}{2}}$ и лежат в полосе $0\leqslant \operatorname {Re} \,s\leqslant 1$, которая называется критической полосой. Согласно гипотезе Римана, они все находятся на критической прямой $\operatorname {Re} \,s={\frac {1}{2}}$.

Представления конкретных значений

ζ(2)

См. также: Ряд обратных квадратов

Из формулы $2\zeta (2m)=(-1)^{m+1}{\frac {(2\pi )^{2m}}{(2m)!}}B_{2m}$, где $\displaystyle B_{2m}$ — число Бернулли, получаем, что $\zeta (2)={\frac {\pi ^{2}}{6}}$.

Другие представления в виде рядов

Ниже приведены другие ряды, сумма которых равна $\zeta (2)$:

${\begin{aligned}\zeta (2)&=3\sum _{k=1}^{\infty }{\frac {1}{k^{2}{\binom {2k}{k}}}}\\\end{aligned}}$

${\begin{aligned}\zeta (2)&=\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{\frac {(i-1)!(j-1)!}{(i+j)!}}\end{aligned}}$

Существуют также представления для $\zeta (2)$ вида формулы Бэйли — Боруэйна — Плаффа, позволяющие в некоторых системах счисления вычислять $k$-й знак его записи без вычисления предыдущих:

${\begin{aligned}\zeta (2)={\frac {27}{4}}\sum _{k=0}^{\infty }{\frac {1}{64^{k}}}\left[{\frac {16}{(6k+1)^{2}}}-{\frac {24}{(6k+2)^{2}}}-{\frac {8}{(6k+3)^{2}}}-{\frac {6}{(6k+4)^{2}}}+{\frac {1}{(6k+5)^{2}}}\right]\end{aligned}}$

${\begin{aligned}\zeta (2)={\frac {4}{9}}\sum _{k=0}^{\infty }{\frac {1}{729^{k}}}\left[{\frac {243}{(12k+1)^{2}}}-{\frac {405}{(12k+2)^{2}}}-{\frac {81}{(12k+4)^{4}}}-{\frac {27}{(12k+5)^{2}}}-\right.\\-\left.{\frac {72}{(12k+6)^{2}}}-{\frac {9}{(12k+7)^{2}}}-{\frac {9}{(12k+8)^{2}}}-{\frac {5}{(12k+10)^{2}}}+{\frac {1}{(12k+11)^{2}}}\right]\end{aligned}}$

Интегральные представления

Дзета-функция представима в виде интеграла при ${\rm {Re}}\,s>0$ :

$\zeta (s+1)={\frac {1}{\Gamma (s+1)}}\int _{0}^{1}{\frac {(-\ln(1-x))^{s}}{x}}dx$

Ниже приведены формулы для $\zeta (2)$ с участием интегралов, полученные с использованием дзета-функции Римана:

${\begin{aligned}\zeta (2)&=-\int _{0}^{1}{\frac {\log x}{1-x}}\,dx\\[6pt]&=\int _{0}^{\infty }{\frac {x}{e^{x}-1}}\,dx\\[6pt]&=\int _{0}^{1}{\frac {(\log x)^{2}}{(1+x)^{2}}}\,dx\\[6pt]&=2+2\int _{1}^{\infty }{\frac {\lfloor x\rfloor -x}{x^{3}}}\,dx\\[6pt]&=\exp \left(2\int _{2}^{\infty }{\frac {\pi (x)}{x(x^{2}-1)}}\,dx\right)\\[6pt]&=\int _{0}^{1}\int _{0}^{1}{\frac {dx\,dy}{1-xy}}\\[6pt]&={\frac {4}{3}}\int _{0}^{1}\int _{0}^{1}{\frac {dx\,dy}{1-(xy)^{2}}}\\[6pt]&=\int _{0}^{1}\int _{0}^{1}{\frac {1-x}{1-xy}}\,dx\,dy+{\frac {2}{3}}.\end{aligned}}$

Цепные дроби

Некоторые из представлений $\zeta (2)$ в виде цепных дробей были получены в связи с аналогичными представлениями для константы Апери $\zeta (3)$, дающими возможность доказать её иррациональность.

$\zeta (2)={\cfrac {2}{1+{\cfrac {1^{4}}{3+{\cfrac {2^{4}}{5+{\cfrac {3^{4}}{7+{\cfrac {\dots }{\dots +{\cfrac {n^{4}}{(2n-1)+\dots }}}}}}}}}}}}$

$\zeta (2)=1+{\cfrac {1}{1+{\cfrac {1^{2}}{1+{\cfrac {1\cdot 2}{1+{\cfrac {2^{2}}{1+{\cfrac {2\cdot 3}{1+{\cfrac {3^{2}}{1+{\cfrac {\dots }{\dots +{\cfrac {n^{2}}{1+{\cfrac {n\cdot (n+1)}{1+\dots }}}}}}}}}}}}}}}}}}$

$\zeta (2)={\cfrac {5}{3+{\cfrac {1^{4}}{25+{\cfrac {2^{4}}{69+{\cfrac {3^{4}}{135+{\cfrac {\dots }{\dots +{\cfrac {n^{4}}{(11n^{2}-11n+3)+\dots }}}}}}}}}}}}$

$\zeta (2)={\frac {5}{3}}+{\cfrac {1}{25+{\cfrac {1^{4}}{69+{\cfrac {2^{4}}{135+{\cfrac {3^{4}}{223+{\cfrac {\dots }{\dots +{\cfrac {n^{4}}{(11n^{2}+11n+3)+\dots }}}}}}}}}}}}$

ζ(3)

Основная статья: Постоянная Апери

Одним из наиболее коротких представлений является $\zeta (3)=-{\frac {\psi ^{(2)}(1)}{2}}$, получаем, что $\zeta (3)\approx 1.2020569031595942853997381615114499907649862923404988817922715553...$ , где $\psi$ — полигамма-функция.

Цепные дроби

Цепная дробь для константы Апери (последовательность A013631 в OEIS) выглядит следующим образом:

$\zeta (3)=[1;4,1,18,1,1,1,4,1,9,9,2,1,1,1,2,7,1,1,7,11,1,1,1,\cdots ]=$

$=1+{\cfrac {1}{4+{\cfrac {1}{1+{\cfrac {1}{18+{\cfrac {1}{1+\ldots }}}}}}}}\;$

Первую обобщённую цепную дробь для константы Апери, имеющую закономерность, открыли независимо Стилтьес и Рамануджан:

$\zeta (3)=1+{\cfrac {1}{4+{\cfrac {1^{3}}{1+{\cfrac {1^{3}}{12+{\cfrac {2^{3}}{1+{\cfrac {2^{3}}{20+{\cfrac {3^{3}}{1+{\cfrac {3^{3}}{28+{\cfrac {\dots }{\dots +{\cfrac {n^{3}}{1+{\cfrac {n^{3}}{4(2n+1)+\dots }}}}}}}}}}}}}}}}}}}}$

Она может быть преобразована к виду:

$\zeta (3)=1+{\cfrac {1}{5-{\cfrac {1^{6}}{21-{\cfrac {2^{6}}{55-{\cfrac {3^{6}}{119-{\cfrac {4^{6}}{225-{\cfrac {\dots }{\dots +{\cfrac {n^{6}}{(2n^{3}+3n^{2}+11n+5)+\dots }}}}}}}}}}}}}}$

Апери смог ускорить сходимость цепной дроби для константы:

$\zeta (3)={\frac {6}{5}}-{\cfrac {1^{6}}{117-{\cfrac {2^{6}}{535-{\cfrac {3^{6}}{1436-{\cfrac {4^{6}}{3105-{\cfrac {\dots }{\dots +{\cfrac {n^{6}}{(34n^{3}+51n^{2}+27n+5)+\dots }}}}}}}}}}}}$

ζ(4)

Из формулы $2\zeta (2m)=(-1)^{m+1}{\frac {(2\pi )^{2m}}{(2m)!}}B_{2m}$, где $\displaystyle B_{2m}$ — число Бернулли, получаем, что $\zeta (4)={\frac {\pi ^{4}}{90}}$.

ζ(5)

Одним из наиболее коротких представлений является $\zeta (5)=-{\frac {\psi ^{(4)}(1)}{24}}$, получаем, что $\zeta (5)\approx 1.0369277551433699263313654864570341680570809195019128119741926779...$ , где $\psi$ — полигамма-функция.

Обобщения

Существует довольно большое количество специальных функций, связанных с дзета-функцией Римана, которые объединяются общим названием дзета-функции и являются её обобщениями. Например:

• Дзета-функция Гурвица:

  $\zeta (s,q)=\sum _{k=0}^{\infty }(k+q)^{-s},$

которая совпадает с дзета-функцией Римана при q = 1 (так как суммирование ведётся от 0, а не от 1).

• Полилогарифм:

  $\mathrm {Li} _{s}(z)=\sum _{k=1}^{\infty }{z^{k} \over k^{s}},$

который совпадает с дзета-функцией Римана при z = 1.

• Дзета-функция Лерха:

  $\Phi (z,s,q)=\sum _{k=0}^{\infty }{\frac {z^{k}}{(k+q)^{s}}},$

которая совпадает с дзета-функцией Римана при z = 1 и q = 1 (так как суммирование ведётся от 0, а не от 1).

• Квантовый аналог (q-аналог).

Аналогичные конструкции

В теории гауссовых интегралов по траекториям возникает задача регуляризации детерминантов. Одним из подходов к её решению является введение дзета-функции оператора. Пусть $A$ — неотрицательно определённый самосопряжённый оператор, имеющий чисто дискретный спектр $\mathrm {spec} A=\mathrm {diag} \{\lambda _{1},\lambda _{2},\dots \}$. Причём существует вещественное число $\alpha >0$, такое, что оператор $(I+A)^{-\alpha }$ имеет след. Тогда дзета-функция $\zeta _{A}(s)$ оператора $A$ определяется для произвольного комплексного числа $s$, лежащего в полуплоскости $\mathrm {Re} s>\alpha$, может быть задана сходящимся рядом

$\zeta _{A}(s)=\sum _{\lambda _{n}\neq 0}{\frac {1}{\lambda _{n}^{s}}}$

Если заданная таким образом функция допускает аналитическое продолжение на область, содержащую некоторую окрестность точки $s=0$, то на её основе можно определить регуляризованный детерминант оператора $A$ в соответствии с формулой

$\det \,'A=e^{-{\frac {d\zeta _{A}}{ds}}(0)}.$

История

Как функция вещественной переменной дзета-функция была введена в 1737 году Эйлером, который и указал её разложение в произведение. Затем эта функция рассматривалась Дирихле и, особенно успешно, Чебышёвым при изучении закона распределения простых чисел. Однако наиболее глубокие свойства дзета-функции были обнаружены позднее, после работы Римана (1859), где дзета-функция рассматривалась как функция комплексного переменного.

См. также

• Список всех дзета-функций

Литература

• Дербишир Дж. Простая одержимость. Бернхард Риман и величайшая нерешённая проблема в математике. — М.: Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2..
• Тахтаджян Л. А. Квантовая механика для математиков / Перевод с английского к.ф.-м.н. С. А. Славнов. — Изд. 2-е. — М.—Ижевск: НИЦ «Регулярная и хаотическая динамика», Ижевский институт компьютерных исследований, 2011. — 496 с. — ISBN 978-5-93972-900-0.
• Янке Е., Эмде Ф., Лёш Ф. Специальные функции: формулы, графики, таблицы / Пер. с 6-го переработанного немецкого издания под ред. Л. И. Седова. — Изд. 3-е, стереотип. — М.: Наука, 1977. — 344 с.

Ссылки

• Jonathan Sondow and Eric W. Weisstein. Riemann Zeta Function (англ.) на сайте Wolfram MathWorld.