Автоморфизм
Автоморфизм — изоморфизм между математическим объектом и им самим; отображение, изменяющее объект с сохранением всех его изначальных свойств. Множество всех автоморфизмов объекта образует группу автоморфизмов, которую можно рассматривать как обобщение группы симметрий объекта.
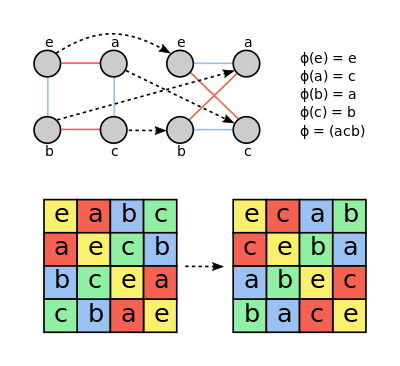
Точное определение автоморфизма зависит от типа математического объекта и контекста. В универсальной алгебре автоморфизм определяется как биективный гомоморфизм алгебраической системы на себя. Тождественное отображение иногда называется тривиальным автоморфизмом; соответственно, нетождественные автоморфизмы называются нетривиальными.
Автоморфизм в теории категорий определяется как эндоморфизм, который также является изоморфизмом.
Если автоморфизмы объекта в категории образуют множество, то они образуют группу относительно операции композиции морфизмов — группу автоморфизмов (или просто , если категория ясна из контекста).
Первый из известных описанных автоморфизмов групп — автоморфизм второго порядка в икосиане, выявленный Гамильтоном в 1856 году[1].
Примеры
правитьВ теории множеств произвольная перестановка элементов множества является автоморфизмом. Группа автоморфизмов также называется симметрической группой на .
Множество целых чисел , рассматриваемое как группа по сложению, имеет единственный нетривиальный автоморфизм: взятие противоположного по знаку. Однако, рассматриваемое как кольцо, оно имеет только тривиальный автоморфизм. Вообще говоря, взятие противоположного является автоморфизмом для любой абелевой группы, но не для кольца или поля.
Автоморфизм группы — это групповой изоморфизм группы на себя; «перестановка» элементов группы, при которой структура остаётся неизменной. Для каждой группы существует естественный гомоморфизм групп , образ которого есть группа внутренних автоморфизмов и ядро которого является центром группы . Таким образом, если группа а имеет тривиальный центр, её можно вложить в собственную группу автоморфизмов[2].
В линейной алгебре эндоморфизмом векторного пространства является линейный оператор . В этом контексте автоморфизм — это обратимый линейный оператор на . Когда векторное пространство конечномерно, группа автоморфизмов совпадает с общей линейной группой . (Алгебраическая структура, состоящая из всех эндоморфизмов[англ.] , сама по себе является алгеброй над тем же полем, что и , чьи обратимые элементы в точности состоят из .)
Автоморфизм полей — биективный кольцевой гомоморфизм поля в себя. В случае рациональных чисел и действительных чисел не существует нетривиальных автоморфизмов этих полей. Некоторые подполя имеют нетривиальные автоморфизмы, которые, однако, не продолжаются на всё (например, потому что эти автоморфизмы не сохраняют свойство числа иметь квадратный корень в ). В случае комплексных чисел существует единственный нетривиальный автоморфизм, переводящий в : комплексное сопряжение, но существует бесконечное (несчётное) множество «диких» автоморфизмов (в предположении аксиомы выбора)[3][4]. Автоморфизмы полей важны для теории расширений полей, в частности, расширений Галуа. В случае расширения Галуа подгруппа всех автоморфизмов , фиксирующих поточечно, называется группой Галуа расширения.
Группа автоморфизмов кватернионов ( ) как кольца — это внутренние автоморфизмы по теореме Скулема — Нётер: отображения вида [5]. Эта группа изоморфна , группе вращений в трёхмерном пространстве.
Группа автоморфизмов октонионов ( ) является исключительной группой Ли G2.
В теории порядков важную роль играет порядковый автоморфизм[англ.] — автоморфзим частично упорядоченных множеств, сохраняющий отношение порядка.
В теории графов автоморфизм графа — это перестановка узлов, сохраняющая рёбра и нерёбра. В частности если два узла соединены ребром, то и их отображения после применения автоморфизма также соединены ребром. В этом случае автоморфизм работает как перенумерация или перестановка вершин графа.
В геометрии автоморфизм называют движением пространства. Также используется специализированная терминология: в категории римановых поверхностей автоморфизм — это биголоморфное отображение (также называемое конформным отображением) с поверхности на себя. Например, автоморфизмы сферы Римана — это преобразования Мёбиуса. Автоморфизм дифференцируемого многообразия есть диффеоморфизм из в себя. Группа автоморфизмов иногда обозначается .
В топологии морфизмы между топологическими пространствами называются непрерывными отображениями, а автоморфизм топологического пространства — это гомеоморфизм пространства в себя. Это пример того, что не всегда достаточно биективности морфизма, чтобы он был изоморфизмом.
Внутренние и внешние автоморфизмы
правитьВ некоторых алгебраических системах, в том числе группах, кольцах и алгебрах Ли, автоморфизмы можно разделить на два типа — внутренние и внешние.
В случае групп внутренние автоморфизмы — это сопряжения при помощи элементов самой группы. Для каждого элемента группы сопряжение при помощи есть операция определяемая как (или ; зависит от источника). Легко проверить, что сопряжение при помощи является автоморфизмом групп. Внутренние автоморфизмы образуют нормальную подгруппу группы , обозначаемую через ; это описывается леммой Гурса[англ.].
Остальные автоморфизмы называются внешними автоморфизмами. Факторгруппу обычно обозначают ; нетривиальные элементы — это смежные классы, содержащие внешние автоморфизмы.
То же самое определение имеет смысл в любом кольце с единицей или в поле, где любой элемент обратим. Для алгебр Ли определение немного отличается.
Литература
править- ↑ Sir William Rowan Hamilton (1856). "Memorandum respecting a new System of Roots of Unity" (PDF). Philosophical Magazine. 12: 446. Архивировано (PDF) 9 октября 2022. Дата обращения: 29 августа 2022.
…so that is a new fifth root of unity, connected with the former fifth root by relations of perfect reciprocity.
- ↑ PJ Pahl, R Damrath. §7.5.5 Automorphisms // Mathematical foundations of computational engineering. — Felix Pahl translation. — Springer, 2001. — P. 376. — ISBN 3-540-67995-2.
- ↑ Yale, Paul B. (May 1966). "Automorphisms of the Complex Numbers" (PDF). Mathematics Magazine. 39 (3): 135–141. doi:10.2307/2689301. JSTOR 2689301. Архивировано (PDF) 8 ноября 2020. Дата обращения: 29 августа 2022.
{{cite journal}}:|archive-date=/|archive-url=несоответствие временной метки; предлагается 8 ноября 2020 (справка) - ↑ Lounesto, Pertti. Clifford Algebras and Spinors. — 2nd. — Cambridge University Press, 2001. — P. 22–23. — ISBN 0-521-00551-5.
- ↑ Handbook of algebra, vol. 3, Elsevier, 2003, p. 453
Ссылки
править- Артамонов В. А. . Глава VI. Универсальные алгебры // Общая алгебра / Под общ. ред. Л. А. Скорнякова. — М.: Наука, 1991. — Т. 2. — С. 295—367. — 480 с. — (Справочная математическая библиотека). — 25 000 экз. — ISBN 5-9221-0400-4.
- Алгебраической системы автоморфизм — статья из Математической энциклопедии. Д. М. Смирнов
- Плоткин Б. И. Группы автоморфизмов алгебраических систем. — М.: Наука, 1966. — 603 с. — 6000 экз.



