Частота Раби

Частота Раби определяется выражением

Поведение во времени населённости возбуждённого состояния $e$ двухуровневого атома для разных ситуаций: без учёта (красная линия) и с учётом (синяя линия) «оттока» населённости на другие, третьи уровни. Населённость уровней в обоих случаях осциллирует с частотой Раби $\Omega _{0}$ Коричневая линия показывает изменение количества атомов при спонтанном распаде с возбуждённого $e$ на спонтанный $g$ уровень.

$\Omega _{0}={\frac {{\vec {d}}\cdot {\vec {\mathcal {E}}}}{\hbar }}$,

$d$ — дипольный момент, ${\mathcal {E}}$ — электрическое поле излучения.

Двухуровневый атом:
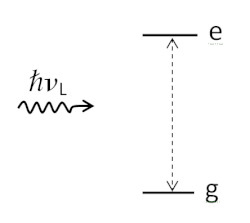
$g$ — основное и $e$ — возбуждённое состояния,
$\hbar \omega _{L}$ — внешнее резонансное излучение с частотой $\omega _{L}$

Из определения следует, что частота Раби количественно описывает взаимодействие резонансного излучения с дипольным моментом атома или молекулы. Под действием резонансного лазерного излучения интенсивностью ${\mathcal {E}}^{2}$ населённость $b_{e}^{2}(t)$ возбуждённого уровня атомной системы осциллирует с частотой Раби $\Omega _{0}$ (иногда их называют биениями Раби) :

$b_{e}^{2}(t)=\sin ^{2}\left({\frac {\Omega _{0}t}{2}}\right)$

Происхождение термина

Термин частота Раби назван именем американского физика, уроженца Галиции, лауреата Нобелевской премии по физике (1944 г.) Исидора Раби. В 1937 году Раби исследовал прецессию магнитного дипольного момента атома со спином 1/2 в магнитном поле и вероятность изменения направления спина атома на противоположное. Оказалось, что «переворот» спина происходит с частотой Раби, величина которой определяется выше приведенной формулой (англ. Rabi problem).

Обобщённая частота Раби

Для нерезонансного света вводится так называемая Обобщённая частота Раби $\Omega ^{'}$.

$\Omega ^{'}={\sqrt {|\Omega _{0}|^{2}+|\Delta |^{2}}}$

где $\Delta =\omega _{L}-\omega _{0}$ есть отстройка лазерного света от резонансного атомного перехода. Обобщённая частота Раби участвует в модели Джейнса-Каммингса, которая является самой простой и в то же время адекватной моделью взаимодействия двухуровнего атома с одной модой квантованного поля в резонаторе с высокой добротностью.

Вакуумная частота Раби

В 1946 г. Парселл обратил внимание на то, что скорость спонтанного излучения двухуровневой системы, помещённой в резонатор, увеличивается пропорционально отношению $Q/V$ по сравнению со скоростью спонтанного излучения в свободном пространстве (эффект Парселла) ; здесь
$Q,~V$ — добротность и объём моды резонатора соответственно. Если добротность резонатора $Q=\omega /\Delta \omega _{c}$ велика, так что $\Omega /\Delta \omega _{c}>1$, то спонтанное излучение становится обратимым, а атом обменивается энергией с созданным им же полем со скоростью, определяемой вакуумной частотой Раби $\Omega _{0}^{v}$.

Предположим, мы имеем пустой высокодобротный одномодовый резонатор. Если в такой резонатор влетает атом, находящийся в возбуждённом состоянии $e$, то вакуумные флуктуации моды резонатора сынициируют спонтанное испускание атомом фотона. В результате атом окажется в основном состоянии $g$. Так как резонатор добротный, то испущенный фотон перепоглотится, и атом снова перейдёт в возбуждённое состояние. Таким образом, вследствие вакуумных флуктуаций поля в резонаторе атом будет осциллировать между его уровнями. Такие осцилляции напоминают поведение атома под действием резонансного лазерного поля, поэтому описанные переходы атома из состояния $g$ в состояние $e$ и обратно, вызванные вакуумными флуктуациями поля в пустом добротном резонаторе, называют вакуумной частотой Раби $\Omega _{0}^{v}$.

Вакуумные осцилляции наблюдались на ридберговских переходах атомов в микроволновых резонаторах и на оптических переходах в микрорезонаторах . Аналитическое выражение для вакуумной частоты Раби имеет вид:

$\Omega _{0}^{v}={\frac {{\hat {d}}{\hat {E}}({\vec {r}})}{\hbar }}$,

где ${\hat {E}}({\vec {r}})={\sqrt {\frac {2\pi \hbar \omega }{V}}}{\vec {e}}u({\vec {r}})(c+c^{\dagger })$,
$V$ — объём моды резонатора, ${\vec {e}}$ — вектор поляризации моды, $\omega$ — частота поля, ${c+c^{\dagger }}$ — операторы рождения и уничтожения фотона, $u({\vec {r}})$ — описывает пространственное распределение моды резонатора.

Одетые состояния

(см. также Сизифово охлаждение#Переменный эффект Штарка)

Смещение атомных уровней $g$ и $e$ под действием лазерного излучения при «голубой» (a) и «красной» (b) настройке частоты лазера. Смещение атомных уровней $\Delta {E}$ противоположно по знаку отстройки частоты лазера

У атома, находящегося в резонансном, когерентном поле, появляются новые зависящие от времени состояния, которые описывают с помощью «одетых» состояний («одетых» полем). В строгом смысле считать их собственными состояниями нельзя, но для описания системы их охотно и успешно используют.

В основе этого понятия лежит известный эффект Штарка. Атом, помещённый во внешнее электрическое поле ${\mathcal {E}}$, меняет свою энергию. В результате энергетические уровни атома смещаются на величину $\Delta {E}={\vec {d}}\cdot {\vec {\mathcal {E}}}$, где ${\vec {d}}$ — дипольный момент атома. В 1955 г. Отлер и Таунс опубликовали работу, в которой представлены результаты исследования эффекта Штарка в интенсивных резонансных полях (см. en:Autler–Townes effect). Оказалось, что под действием переменного электрического поля, в том числе при освещении светом, уровни атома также смещаются. С этого времени этот эффект называют «переменным эффектом Штарка»:

$\Delta {E}=-c^{2}{\frac {\Omega _{0}^{2}}{2\delta }}$

где $\Omega _{0}={\frac {{\vec {d}}\cdot {\vec {\mathcal {E}}}}{\hbar }}$ — частота Раби, $\delta$ — отстройка частоты лазера от атомного резонанса $\nu _{L}$ В 1977 году К. Коэн-Таннуджи ввёл понятие одетые состояния.

π/2 и π импульсы

Если приложить импульс поля длительностью $\tau$ так, что $\Omega _{0}\times \tau =\pi$, то атом перейдёт из состояния $g$ в состояние $e$ (см. формулу для $b^{2}(t)$). Такой импульс называют $\pi$-импульс.

В случае, когда частица в результате импульсного воздействия за время $\tau ={\frac {\pi }{2\Omega _{0}}}$ перейдёт в суперпозиционное состояние ${\frac {g+e}{\sqrt {2}}}$, такой импульс называют $\pi /2$-импульсом.

Литература

• В. С. Летохов, В. П. Чеботаев. Принципы нелинейной лазерной спектроскопии. — М.: Наука, 1975. Рецензия Е. Б. Александрова
• М. О. Скалли, М. С. Зубайри (M.O. Scully, M.S. Zubairy), Квантовая оптика, Перевод с английского под ред В. В. Самарцева, — М.: Физматлит, 2003 г.

УДК 535(082) ББК 22.34 52487

• Serge Haroche and Daniel Kleppner, Cavity Quantum Electrodynamics, Physics Today, p24, January (1989),
• В. М. Акулин, Н. В. Карлов. Интенсивные резонансные взаимодействия в квантовой электронике. – М.: Наука, 1987.