Строго нормированное пространство

В математике строго нормированные пространства — это важный подкласс нормированных пространств, по своей структуре близких к гильбертовым. Для таких пространств решён вопрос единственности аппроксимаций, и это свойство находит широкое применение в вопросах вычислительной математики и математической физике. Кроме того, в строго нормированном пространстве отрезок соединяющий две точки произвольной сферы, будет целиком лежать строго внутри (за исключением граничных точек) открытого шара, ограниченного данной сферой.

Нормированное пространство X называют строго нормированным (или строго выпуклым), если для произвольных $x,y\in X$ , удовлетворяющих условию $\|x+y\|=\|x\|+\|y\|$ , найдётся такое $\lambda \in \mathbb {R}$ , что $y=\lambda x$ .

Свойства строго нормированных пространств

Пусть X — строго нормированное пространство, а L — линейное подпространство. Тогда для $\forall x\in X$ найдется не более одного элемента $u\in L$ такого, что $\rho (x,L)=\|x-u\|$ .

Элемент $u$ называют элементом наилучшего приближения x элементами из L. Существование элемента наилучшего приближения обеспечивает следующая теорема.

Теорема. Пусть X — нормированное пространство, а L — конечномерное линейное подпространство. Тогда для $\forall x\in E$ существует элемент наилучшего приближения $u\in L$ .

При этом в нормированном, но не строго нормированном пространстве, элемент наилучшего приближения, вообще говоря, не единственен.

Каждый шар строго нормированного пространства — строго выпуклое множество. Верно и обратное, если в нормированном пространстве каждый шар — строго выпуклое множество, то данное пространство является строго нормированным.
Нормированное пространство X является строго нормированным тогда и только тогда, когда из условия $\forall x,y\in X:\|x\|=1,\|y\|=1,x\neq y$ всегда следует что $\|x+y\|<2$ .

Примеры строго нормированных пространств

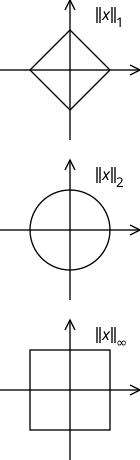
$\mathbb {R} ^{2}$ с нормой $\|\mathbf {x} \|_{2}={\sqrt {x_{1}^{2}+x_{2}^{2}}}$ . Однако нормы $\|\mathbf {x} \|_{1}=|x_{1}|+|x_{2}|$ и $\|\mathbf {x} \|_{\infty }=\max\{|x_{1}|,|x_{2}|\}$ на $\mathbb {R} ^{2}$ , эквивалентные норме $\|\cdot \|_{2}$ не порождают строго нормированное пространство (см. рисунок).
$L_{p}$ , где $1<p<\infty$ . Этот факт следует из неравенства Юнга, которое используется при выводе неравенств Гёльдера и Минковского.
Гильбертовы пространства

Литература

Треногин В. А. Функциональный анализ. — М.: Наука, 1980. — 495 с.
Функциональный анализ / редактор Крейн С. Г. — 2-е, переработанное и дополненное. — М.: Наука, 1972. — 544 с. — (Справочная математическая библиотека).