Стодвадцатиячейник
| Стодвадцатиячейник | |
|---|---|
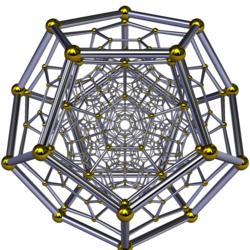 Диаграмма Шлегеля: проекция (перспектива) стодвадцатиячейника в трёхмерное пространство | |
| Тип | Правильный четырёхмерный политоп |
| Символ Шлефли | {5,3,3} |
| Ячеек | 120 |
| Граней | 720 |
| Рёбер | 1200 |
| Вершин | 600 |
| Вершинная фигура | Правильный тетраэдр |
| Двойственный политоп | Шестисотячейник |
Пра́вильный стодвадцатияче́йник, или просто стодвадцатияче́йник[1] — один из шести правильных многоячейников в четырёхмерном пространстве. Известен также под другими названиями: гекатоникосахор (от др.-греч. ἑκατόν — «сто», εἴκοσι — «двадцать» и χώρος — «место, пространство»), гипердодека́эдр (поскольку является четырёхмерным аналогом додекаэдра), додекаплекс (то есть «комплекс додекаэдров»), полидодека́эдр. Двойственен шестисотячейнику.
Открыт Людвигом Шлефли в середине 1850-х годов[2]. Символ Шлефли стодвадцатиячейника — {5,3,3}.
Все 9 его звёздчатых форм — правильные звёздчатые многоячейники. Из 10 правильных звёздчатых многоячейников лишь один не является звёздчатой формой стодвадцатиячейника.
Описание
правитьОграничен 120 трёхмерными ячейками — одинаковыми додекаэдрами. Угол между двумя смежными ячейками равен в точности
Его 720 двумерных граней — одинаковые правильные пятиугольники. Каждая грань разделяет 2 примыкающие к ней ячейки.
Имеет 1200 рёбер равной длины. На каждом ребре сходятся по 3 грани и по 3 ячейки.
Имеет 600 вершин. В каждой вершине сходятся по 4 ребра, по 6 граней и по 4 ячейки.
В координатах
правитьСтодвадцатиячейник можно разместить в декартовой системе координат так, чтобы:
- координаты 24 его вершин были всевозможными перестановками чисел
- координаты 64 вершин — всевозможными перестановками
- координаты 64 вершин — всевозможными перестановками где — отношение золотого сечения;
- координаты 64 вершин — всевозможными перестановками
- координаты 96 вершин — всевозможными чётными перестановками
- координаты 96 вершин — всевозможными чётными перестановками
- координаты остальных 192 вершин — всевозможными чётными перестановками
Начало координат будет при этом центром симметрии многоячейника, а также центром его вписанной, описанной и полувписанных трёхмерных гиперсфер.
Проекция вращающегося стодвадцатиячейника в трёхмерное пространство
правитьОртогональные проекции на плоскость
правитьМетрические характеристики
правитьЕсли стодвадцатиячейник имеет ребро длины то его четырёхмерный гиперобъём и трёхмерная гиперплощадь поверхности выражаются соответственно как
Радиус описанной трёхмерной гиперсферы (проходящей через все вершины многоячейника) при этом будет равен
радиус внешней полувписанной гиперсферы (касающейся всех рёбер в их серединах) —
радиус внутренней полувписанной гиперсферы (касающейся всех граней в их центрах) —
радиус вписанной гиперсферы (касающейся всех ячеек в их центрах) —
Примечания
править- ↑ Д. К. Бобылёв. Четырехмерное пространство // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- ↑ George Olshevsky. Hecatonicosachoron // Glossary for Hyperspace.
Ссылки
править- Weisstein, Eric W. Стодвадцатиячейник (англ.) на сайте Wolfram MathWorld.
- Построение стодвадцатиячейника на YouTube
- Главы 3 и 4: Четвертое измерение. Dimensions. dimensions-math.org. Архивировано 4 марта 2015 года.