Прямая Эйлера

Пряма́я Э́йлера — прямая, проходящая через центр описанной окружности, центроид и ортоцентр треугольника.

Прямая Эйлера (красная) проходит через центр описанной окружности треугольника, его ортоцентр, центр тяжести и центр окружности девяти точек

Прямая Эйлера выделена зелёным цветом. $H$ — ортоцентр; $M$ — центроид (точка пересечения медиан); $O$ — центр описанной окружности; $O_{9}$ — центр окружности девяти точек

Свойства

• Прямая Эйлера проходит через:
  • Центроид треугольника
  • Ортоцентр треугольника
  • Точку пересечения серединных перпендикуляров к сторонам треугольника (центр описанной окружности)
  • Центр окружности девяти точек
  • Точка Эксетера X(22)
  • Теорема Эйлера. Точка пересечения медиан M лежит на прямой Эйлера и делит отрезок между центром описанной окружности O и ортоцентром H в отношении 1:2 ($OM:MH=1:2$).
  • Прямая $X(485)X(486)$, проходящая через две точки Вектена $X(485)$ и $X(486)$, пересекает прямую Эйлера в центре девяти точек треугольника $ABC$.
  • Уравнение прямой Эйлера в трилинейных координатах есть

    $x\sin 2A\sin(B-C)+y\sin 2B\sin(C-A)+z\sin 2C\sin(A-B)=0.$

• На одной прямой лежат также точки пересечения прямых, содержащих стороны ортотреугольника, с прямыми, содержащими стороны треугольника. Эта прямая называется ортоцентрической осью, она перпендикулярна прямой Эйлера.

Точка Шиффлера $S_{p}$ — точка пересечения прямых Эйлера трёх треугольников: $\triangle BCI,\;\triangle CAI$и $\triangle ABI$

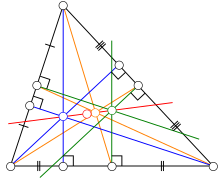
• Теорема Шиффлера утверждает следующее: Если в треугольнике ABC с центром вписанной окружности I рассмотреть три треугольника BCI, CAI и ABI, то их три (первые) прямые Эйлера, а также (первая) прямая Эйлера треугольника ABC (все четыре прямые) пересекутся в одной точке — в точке Шиффлера Sp (см. рис. справа).

Вторая прямая Эйлера (прямая Эйлера — Нагеля)

Указанную выше прямую Эйлера иногда называют (первой) обобщённой прямой Эйлера. На этой прямой лежат 4 точки:

• центроид данного треугольника (он же — центроид дополнительного треугольника, и он же — центроид антидополнительного треугольника)
• ортоцентр данного треугольника ABC
• центр описанной окружности данного треугольника ABC (он же — центр окружности Эйлера антидополнительного треугольника A"B"C")
• центр окружности Эйлера данного треугольника ABC
• Некоторые авторы добавляют ещё точку Лоншана L — точку зеркального отражения ортоцентра треугольника ABC относительно его центра описанной окружности. Эта точка — ортоцентр антидополнительного треугольника.

Вторую прямую Эйлера или прямую Эйлера — Нагеля определяет следующая Теорема Хузеля.

• Теорема Хузеля уточнённая(Housel). Центр тяжести (G) данного треугольника ABC (центроид), центр вписанной окружности (I), его точка Нагеля (M) и центр (S) круга, вписанного в дополнительный треугольник A’B’C' (или в Центр Шпикера), лежат на одной прямой. Более того,

$\left\{{\begin{matrix}IS=SM;\\IG=2GS;\\MG=2IG.\end{matrix}}\right.$

На этой прямой лежат 4 точки:

• центроид(G) данного треугольника (он же — центроид дополнительного треугольника, и он же — центроид антидополнительного треугольника).
• точка Нагеля (M) данного треугольника ABC (она же — центр круга, вписанного в антидополнительный треугольник A"B"C")
• центр вписанной окружности (I) данного треугольника ABC
• центр (S) круга, вписанного в дополнительный треугольник A’B’C', называемый также центром Шпикера.

• Все обобщённые прямые Эйлера обязательно проходят через центроид данного треугольника, являющегося одновременно центроидами дополнительного треугольника и антидополнительного треугольника.

Перспектор Госсарда и прямые Эйлера

Если брать у треугольника ABC любую пару сторон, а третьей стороной брать первую прямую Эйлера треугольника ABC, то перебором трёх вариантов можно построить три треугольника. Их первые прямые Эйлера образуют треугольник AgBgCg, конгруэнтный треугольнику ABC (равный ему, но повëрнутый на некоторый угол). Три пары отрезков, соединяющие сходственные вершины этих двух конгруэнтных треугольников пересекутся в точке Pg, называемой перспектором Госсарда.

Ссылка

Перспектор Госсарда (Gossard Perspector) http://faculty.evansville.edu/ck6/tcenters/recent/gosspersp.html

История

Теорема Эйлера была доказана в 1765 году Л. Эйлером. Тогда же он обнаружил и тот факт, что середины сторон треугольника и основания его высот лежат на одной окружности — окружности Эйлера.

См. также

• Список объектов, названных в честь Леонарда Эйлера
• Прямая Обера
• Прямая Симсона

Литература

• Leonhard Euler. Solutio facilis problematum quorundam geometricorum difficillimorum // Novi Commentarii academiae scientiarum imperialis Petropolitanae. 1767, т. 11. — С. 103—123. Перепечатано в Opera Omnia, ser. I, vol. XXVI, pp. 139—157, Societas Scientiarum Naturalium Helveticae, Lausanne, 1953, MR0061061.
• Дм. Ефремов. Новая геометрия треугольника. — 1902.
• Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
• Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 96—97. — 383 с. — ISBN 5-09-001287-3..
• Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание.. — М.: Учпедгиз, 1962. — 153 с.