Полугиперкуб - это геометрическое тело, получаемое в результате альтернации (удаления половины вершин (чередующихся)) гиперкуба. В пространствах с размерностью 3 и 4 полугиперкубы - это правильные политопы. В пространствах размерностью 5 и выше полугиперкубы - неправильные, но однородные политопы, то есть их трёхмерные грани - правильные многоугольники, хотя их гиперграни не являются правильными политопами. При этом пятимерный полугиперкуб, называющийся полупентеракт, является полуправильным политопом (это означает, что его гиперграни - разные правильные политопы).
Название полугиперкуба строится так: к префиксу полу- добавляется название исходного гиперкуба.
Вершинная фигура полугиперкуба - полностью усечённый симплекс размерности n-1, где n - размерность самого полугиперкуба. Частные случаи:
| Число измерений n | Гиперкуб | Изображение гиперкуба | Полугиперкуб | Изображение полугиперкуба |
|---|---|---|---|---|
| 2 | квадрат | 
|
отрезок | 
|
| 3 | куб | 
|
правильный тетраэдр | 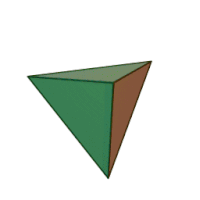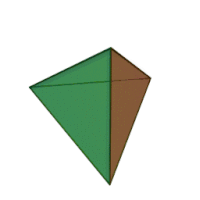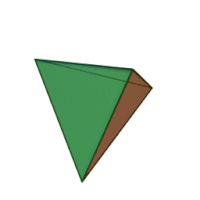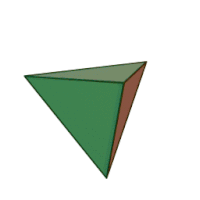
|
| 4 | тессеракт | 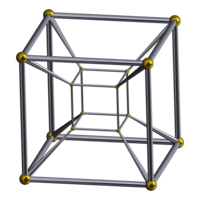
|
шестнадцатиячейник | 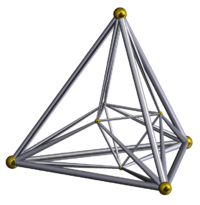
|
| 5 | пентеракт | 
|
полупентеракт | 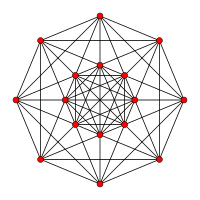
|
| 6 | гексеракт | 
|
полугексеракт | 
|
| 7 | гептеракт | 
|
полугептеракт | 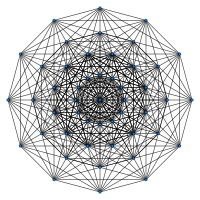
|
| 8 | октеракт | 
|
полуоктеракт | 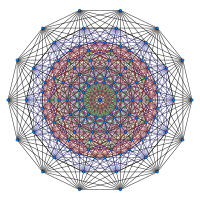
|
| 9 | эннеракт | 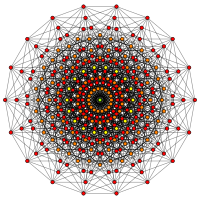
|
полуэннеракт | 
|
| 10 | декеракт | 
|
полудекеракт | 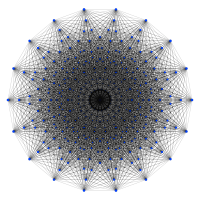
|
См. также
правитьЛитература
править- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900