Конъю́нкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И»[1].
| Конъюнкция | |
|---|---|
| И, AND | |
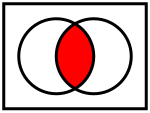 Диаграмма Венна | |
| Определение | |
| Таблица истинности | |
| Логический вентиль |
|
| Нормальные формы | |
| Дизъюнктивная | |
| Конъюнктивная | |
| Полином Жегалкина | |
| Принадлежность предполным классам | |
| Сохраняет 0 | Да |
| Сохраняет 1 | Да |
| Монотонна | Да |
| Линейна | Нет |
| Самодвойственна | Нет |
Конъюнкция может быть бинарной операцией (т. e. иметь два операнда), тернарной операцией (т. e. иметь три операнда), или n-арной операцией (т. e. иметь n операндов).
Инверсией конъюнкции является штрих Шеффера.
Обозначения
правитьНаиболее часто встречаются следующие обозначения для операции конъюнкции:
(в случае использования точки, как знака логического умножения, этот знак, как и при обычном умножении в алгебре, может быть опущен: [1]).
При этом обозначение , рекомендованное стандартом ISO 31-11, наиболее широко распространено в современной математике и математической логике, где оно, впрочем, конкурирует со знаком амперсанда &[1]; последний, появившись ещё в I веке до н. э. как графическое сокращение (лигатура) латинского союза et ‘и’, уже Якобом и Иоганном Бернулли в 1685 году использовался в качестве логической связки (у них он, однако, связывал не высказывания, а понятия)[2][3]. Джордж Буль (а за ним — и другие пионеры систематического применения символического метода к логике: У. С. Джевонс, Э. Шрёдер, П. С. Порецкий) обозначал конъюнкцию знаком — как обычное умножение[4]. Символ ⋀ (перевёрнутый знак дизъюнкции) в качестве обозначения конъюнкции был предложен Арендом Гейтингом (1930)[5].
Обозначение ⋀ для конъюнкции было использовано и в раннем языке программирования Алгол 60[6]. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для конъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения .AND. и & (с возможностью замены последнего на ключевое слово AND)[7]; в языках Паскаль и Ада используется зарезервированное слово and[8][9]; в языках C и C++ применяются обозначения & для побитовой конъюнкции и && для логической конъюнкции[10]).
Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что ), оказывается, что Таким образом, конъюнкция оказывается частным случаем операции вычисления минимума; это открывает наиболее естественный способ определить операцию конъюнкции в системах многозначной логики (хотя иногда рассматривают и другие способы обобщения конъюнкции — например, такой: в случае k-значной логики, в которой множество значений истинности представлено начальным отрезком полугруппы натуральных чисел)[11][12].
Булева алгебра
правитьОпределение.
Логическая функция MIN в двухзначной (двоичной) логике называется конъюнкция (логи́ческое «И», логи́ческое умноже́ние или просто «И»).
Правило: результат равен наименьшему операнду.
Описание.
В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества . Результат также принадлежит множеству . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений может использоваться любая другая пара подходящих символов, например или или «ложь», «истина», но при таком обозначении необходимо дополнительно доопределять старшинство, например, , при цифровом обозначении старшинство естественно .
Правило: результат равен , если все операнды равны ; во всех остальных случаях результат равен .
Таблицы истинности:
для бинарной конъюнкции
для тернарной конъюнкции
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
Конъюнкция коммутативна, ассоциативна и дистрибутивна по отношению к слабой дизъюнкции[13].
Многозначная логика
правитьОперации, называемой в двоичной логике конъюнкция, в многозначных логиках обычно сопоставляется операция минимум: , где а — значность логики; впрочем, возможны и другие варианты обобщения обычной конъюнкции на многозначный случай. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов и .
Название этой операции минимум имеет смысл в логиках с любой значностью, в том числе и в двоичной логике, а названия конъюнкция, логи́ческое «И», логическое умноже́ние и просто «И» характерны для двоичной логики, а при переходе к многозначным логикам используются реже.
Классическая логика
правитьВ классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции:
С помощью этих аксиом можно доказать другие формулы, содержащие операцию конъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
Схемотехника
правитьЛогический элемент, реализующий функцию конъюнкции, называется схемой совпадения[13]. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах есть «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе есть «0»
Теория множеств
правитьС точки зрения теории множеств, конъюнкция аналогична операции пересечения.
Программирование
правитьВ компьютерных языках используется два основных варианта конъюнкции: логическое «И» и побитовое (поразрядное) «И». Например, в языках C/C++ логическое «И» обозначается символом «&&», а побитовое — символом «&». В терминологии, используемой в C#, операцию «&» принято называть логическим «И», а операцию «&&» — условным «И», поскольку значения операндов являются условиями для продолжения вычисления. В языках Pascal/Delphi оба вида конъюнкции обозначаются с использованием ключевого слова «and», а результат действия определяется типом операндов. Если операнды имеют логический тип (например, Boolean) — выполняется логическая операция, если целочисленный (например, Byte) — поразрядная.
Логическое «И» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата или . Например:
if (a & b & c)
{
/* какие-то действия */
};
Сравнение в данном случае будет продолжаться до конца выражения, независимо от промежуточных результатов. Принцип работы условного «И» в аналогичной ситуации:
a = false; b = true; c = true;
if (a && b && c)
{
/* какие-то действия */
};
Проверка истинности выражения в данном случае остановится после проверки переменной a, так как дальнейшее сравнение не имеет смысла.
Результат будет равен , если оба операнда равны (для числовых типов не равны ). В любом другом случае результат будет равен .
При этом применяется стандартное соглашение: если значение левого операнда равно , то значение правого операнда не вычисляется (вместо может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приёмом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую
{$B-}
или выключающую
{$B+}
подобное поведение. Например, если левый операнд проверяет возможность вычисления правого операнда:
if (a != 0 && b / a > 3)
{
/* какие-то действия */
};
В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдёт деления на ноль.
Побитовое «И» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | |
| b = | |
| то | |
| a И b = |
Связь с естественным языком
правитьЧасто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как , а «ложь» как . При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом». Отличие логики естественного языка от математической выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребёнка» — не то же самое, что «Мэри родила ребёнка и вышла замуж».
См. также
правитьПримечания
править- ↑ 1 2 3 Кондаков, 1975, с. 264—266, 534—536.
- ↑ Ampersand. // Website Online Etymology Dictionary. Дата обращения: 7 февраля 2016. Архивировано 18 февраля 2011 года.
- ↑ Кондаков, 1975, с. 67.
- ↑ Стяжкин Н. И. Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 321, 348, 352, 368.
- ↑ Earliest Uses of Symbols of Set Theory and Logic. // Website Jeff Miller Web Pages. Дата обращения: 7 февраля 2016. Архивировано 21 августа 2011 года.
- ↑ Кондаков, 1975, с. 30.
- ↑ Пратт Т. Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
- ↑ Грогоно П. Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
- ↑ Вегнер П. Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
- ↑ Эллис М.[англ.], Строуструп Б. Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
- ↑ Яблонский С. В. Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
- ↑ Рвачёв В. Л. Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
- ↑ 1 2 Словарь по кибернетике. 2-е изд / Под ред. В. С. Михалевича. — Киев: Украинская советская энциклопедия, 1989. — 751 с. — ISBN 5-88500-008-5.
Литература
править- Кондаков Н. И. Логический словарь-справочник. 2-е изд. — М.: Наука, 1975. — 720 с.

