Центростремительное ускорение

Центростреми́тельное (норма́льное) ускоре́ние — составляющая ускорения тела, характеризующая быстроту изменения направления вектора скорости (вторая составляющая, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, с чем и связан термин. Обозначается символом, выбранным для ускорения, с добавлением значка «нормальное»: ${\vec {a}}_{n}$ (реже ${\vec {w}}_{n}$ ); в системе СИ измеряется в м/с².

Пример движения с ненулевым центростремительным ускорением — движение по окружности (в таком случае ${\vec {a}}_{n}$ направлено к центру окружности).

В классической механике нормальное ускорение вызывается компонентами сил, направленными ортогонально вектору скорости. Например, движение космического объекта на орбите характеризуется центростремительным ускорением, вызванным гравитацией. Составляющая суммы сил, обусловливающая наличие нормального ускорения, называется центростремительной силой. Связанное понятие для неинерциальных систем отсчёта — центробежная сила.

Осестремительное ускорение, рассматриваемое в случаях вращения тела вокруг оси, в проекции на плоскость, перпендикулярную оси, предстаёт как центростремительное.

Общая формула

Нормальное ускорение $a_{n}$ вычисляется по формуле

a_{n}={\frac {v^{2}}{R}}

или (с использованием соотношения $v=\omega R$ )

a_{n}=\omega ^{2}R

,

где $v$ — (мгновенная) линейная скорость движения по траектории, $\omega$ — (мгновенная) угловая скорость движения относительно центра кривизны траектории, $R$ — радиус кривизны траектории в данной точке.

Выражения могут быть переписаны в векторном виде:

\mathbf {a} _{n}={\frac {v^{2}}{R}}\mathbf {n} =\omega ^{2}R\mathbf {n}

.

Здесь $\mathbf {n}$ — единичный вектор, направленный от данной точки траектории к центру кривизны траектории.

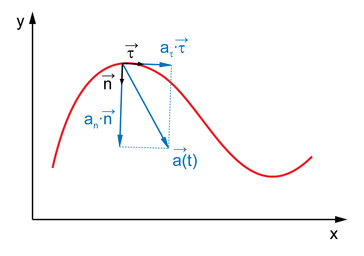
Эти формулы применимы как к частной ситуации равномерного движения ( $|{\vec {v}}|=\,$ const), так и к произвольному случаю. В равномерном случае нормальное ускорение совпадает с полным. В общем же случае нормальное ускорение — это лишь компонента вектора ${\vec {a}}$ , перпендикулярная траектории движения (вектору ${\vec {v}}$ ), а в полный вектор ускорения входит ещё и тангенциальная составляющая $a_{\tau }=dv/dt$ , сонаправленная касательной к траектории движения^[1].

Вывод формулы

Для разложения ускорения на тангенциальное и нормальное можно продифференцировать по времени вектор скорости, представленный в виде $\mathbf {v} =v\,\mathbf {\tau }$ через единичный вектор касательной $\mathbf {\tau }$ :

\mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d(v\mathbf {\tau } )}{dt}}={\frac {\mathrm {d} v}{\mathrm {d} t}}\,\mathbf {\tau } +v{\frac {d\mathbf {\tau } }{dt}}=\mathbf {a} _{\tau }+v{\frac {d\mathbf {\tau } }{dl}}{\frac {dl}{dt}}=\mathbf {a} _{\tau }+v^{2}{\frac {d\mathbf {\tau } }{dl}}=\mathbf {a} _{\tau }+{\frac {v^{2}}{R}}{\frac {d\mathbf {\tau } }{d\varphi }}=\mathbf {a} _{\tau }+{\frac {v^{2}}{R}}\,\mathbf {n}

.

Здесь первое слагаемое — тангенциальное ускорение, а второе — нормальное ускорение. Через $\mathbf {n}$ обозначен единичный вектор нормали, $R$ — радиус кривизны траектории в рассматриваемой точке, $dl$ — элемент длины траектории. Малый участок любой кривой может считаться дугой окружности, причём её радиус и есть радиус кривизны $R$ . В цепочке преобразований использованы очевидные соотношения $dl/dt=v$ и $dl=R\,d\varphi$ (где $d\varphi$ — малый угол поворота вокруг центра кривизны).

Равенство $d\mathbf {\tau } /d\varphi =\mathbf {n}$ вытекает из геометрических соображений. Разность $\Delta \mathbf {\tau } =\mathbf {\tau } '-\mathbf {\tau }$ единичных касательных векторов в рассматриваемой ( $\mathbf {\tau }$ ) и близкой к ней ( $\mathbf {\tau } '$ ) точках траектории составляет по величине $2\sin(\Delta \varphi /2)$ , где $\Delta \varphi$ — угол между $\mathbf {\tau } '$ и $\mathbf {\tau }$ . Эта разность направлена под углом $\Delta \varphi /2$ к нормали $\mathbf {n}$ в рассматриваемой точке. При малости $\Delta \varphi$ будет совпадение с вектором нормали $\mathbf {n}$ . Также при малости $\Delta \varphi$ возможно разложении синуса в ряд Тейлора. В результате придём к $\Delta \mathbf {\tau } =\Delta \varphi \,\mathbf {n}$ или, для бесконечно малых, $d\mathbf {\tau } /d\varphi =d\varphi /d\varphi \,\mathbf {n}$ .

О радиусе кривизны

Вычисление радиуса кривизны и координат центра кривизны траектории является математической задачей (см. Кривизна). Если кривая задана уравнением $y=f(x)$ , то радиус её кривизны в точке ( $x$ , $y$ ) находится как^[2]

R={\frac {(1+f'^{2})^{3/2}}{|f''|}}

,

а положение центра кривизны — по формулам^[2]

\xi =x-{\frac {f'(1+f'^{2})}{f''}},\qquad \eta =y+{\frac {1+f'^{2}}{f''}}

.

Единичный вектор нормали в таком случае составит ( ${\vec {i}}$ , ${\vec {j}}$ — орты)

{\vec {n}}={\frac {\xi -x}{R}}\,{\vec {i}}+{\frac {\eta -y}{R}}\,{\vec {j}}

.

Если известна зависимость радиус-вектора материальной точки от времени ${\vec {r}}(t)$ (с математической точки зрения это означает задание траектории в параметрическом виде), то радиус кривизны можно найти через ускорение:

R={\frac {v^{2}}{\sqrt {a^{2}-a_{\tau }^{2}}}}

,

где ${\vec {a}}=d{\vec {v}}/dt$ и $a_{\tau }=dv/dt$ ; предварительно находится скорость как ${\vec {v}}=d{\vec {r}}/dt$ . Центр кривизны в общем случае не будет совпадать с началом отсчёта радиус-вектора.

Мотивация, замечания

Разложение вектора ускорения на компоненты — одну (тангенциальную) вдоль касательной к траектории и другую (нормальную) ортогональную ей — может быть удобным и полезным. При движении с постоянной по модулю скоростью тангенциальная составляющая становится равной нулю, то есть в этом важном частном случае остается только нормальная составляющая. Кроме того, каждая из этих составляющих имеет ярко выраженные собственные свойства и структуру, и нормальное ускорение содержит в структуре своей формулы достаточно важное и нетривиальное геометрическое наполнение. Крайне важен также частный случай движения по окружности.

Абсолютная величина тангенциального ускорения зависит только от путевого ускорения, совпадая с его абсолютной величиной, в отличие от абсолютной величины нормального ускорения, которая от путевого ускорения не зависит, зато зависит от путевой скорости.

История понятия

Первым правильные формулы для центростремительного ускорения (или центробежной силы) получил, по-видимому, Гюйгенс. Практически с этого времени рассмотрение центростремительного ускорения входит в обычную технику решения механических задач.

Несколько позже эти формулы сыграли существенную роль в открытии закона всемирного тяготения (формула центростремительного ускорения использовалась для получения закона зависимости гравитационной силы от расстояния до источника гравитации, исходя из выведенного из наблюдений третьего закона Кеплера).

К XIX веку рассмотрение центростремительного ускорения становится уже совершенно рутинным как для чистой науки, так и для инженерных приложений.

См. также

Примечания

↑ Как видно из формулы, при движении с постоянной путевой скоростью — тангенциальное ускорение попросту равно нулю.
↑ ¹ ² Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», c. 368-370. (неопр.) Дата обращения: 17 апреля 2021. Архивировано 15 января 2022 года.

[1] Как видно из формулы, при движении с постоянной путевой скоростью — тангенциальное ускорение попросту равно нулю.

[kriv-2] ¹ ² Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», c. 368-370. (неопр.) Дата обращения: 17 апреля 2021. Архивировано 15 января 2022 года.

[1]

[2]