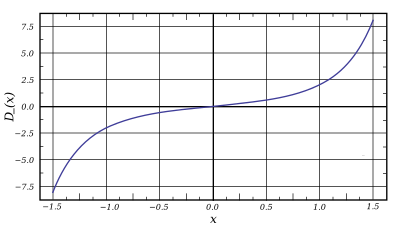
В математике функция Доусона, или интеграл Доусона (названная по имени Генри Гордона Доусона) — неэлементарная функция действительного переменного:

Свойства
править- Общие свойства
- Нечётная функция: .
- Производная: .
- Неопределённый интеграл: , где - обобщённая гипергеометрическая функция.
- Является дробной производной обратной экспоненты: .
- Имеет максимум в точке, являющейся решением уравнения : . Дроби задаются последовательностями цифр последовательность 133841 в OEIS и последовательность 133842 в OEIS.
- Имеет точку перегиба: (последовательность 133843 в OEIS).
- Раскладывается в цепные дроби:
- Функция ошибок
Функция Доусона тесно связана с интегралом ошибок erf:
где erfi является мнимой частью функции ошибок, erfi(x) = −i erf(ix).
Для |x|, близких к нулю, F(x) ≈ x, а для |x| больших, F(x) ≈ 1/(2x). Более точно, вблизи начала координат имеет место разложение в ряд:
(этот степенной ряд сходится при всех x) и, около , имеется асимптотическое разложение:
(которое, напротив, для всех x представляет собой расходящийся ряд).
- Альтернативное определение
F(x) удовлетворяет обыкновенному дифференциальному уравнению
с начальным условием F (0) = 0.
Обобщения
правитьИногда используют другое обозначение для функции Доусона: , тогда вводят "симметричную" её в нотации: ; в таких обозначениях:
- и
- .
См. также
правитьЛитература
править- Temme, N. M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255
Ссылки
править- Cephes — Библиотека математических функций на C и C++
- Weisstein, Eric W. Интеграл Доусона (англ.) на сайте Wolfram MathWorld.
- Функция ошибок
- Реализации функции Доусона


