Уравнение Масона — Вивера
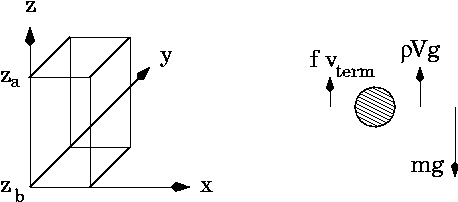
Уравнение Масона — Вивера описывает седиментацию и диффузию растворённого вещества под действием однородной силы, обычно гравитационного поля.[1] Предполагая, что сила тяжести направлена по оси , уравнение Масона — Вивера записывают в виде
- ,
где
— время,
— концентрация растворённого вещества (молей на единицу длины в направлении ),
— седиментационный коэффициент растворённого вещества,
— ускорение свободного падения (предполагается постоянным).
Уравнение Масона — Вивера дополняется граничными условиями
на верхней и нижней границах ячейки, обозначенных как и , соответственно. Эти граничные условия соответствуют тому условию, что растворённое вещество не покидает ячейку, то есть что поток равен нулю. Ячейка предполагается прямоугольной и выровненной относительно координатных осей, таким образом что поток через боковые стенки равен нулю. Отсюда следует, что полное количество растворённого вещества в ячейке
сохраняется, то есть .
Это заготовка статьи по физике. Помогите Википедии, дополнив её. |
Примечания
править- ↑ Mason, M; Weaver W. The Settling of Small Particles in a Fluid (неопр.) // Physical Review. — 1924. — Т. 23. — С. 412—426. — doi:10.1103/PhysRev.23.412.











