Закон больших чисел

Закон больших чисел (ЗБЧ) в теории вероятностей — принцип, описывающий результат выполнения одного и того же эксперимента много раз. Согласно закону, среднее значение конечной выборки из фиксированного распределения близко к математическому ожиданию этого распределения.

Иллюстрация закона больших чисел с использованием определённой серии бросков одной игральной кости. По мере увеличения количества бросков в серии среднее значение всех исходов (выпавших значений) стремится к 3,5. В то время как разные серии бросков дадут различный профиль этой линии при небольшом количестве бросков (слева), после значительного количества бросков (справа) они окажутся очень похожи

Другими словами, чем больше объём выборки, чем чаще проводятся измерения какого-либо параметра, тем выше вероятность того, что результаты окажутся близкими к ожидаемым.

Закон больших чисел важен, поскольку он гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.

Важно помнить, что закон применим только тогда, когда рассматривается большое количество испытаний.

Примеры

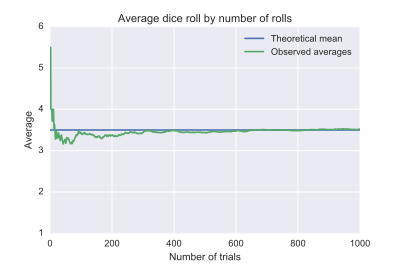
Например, рассмотрим бросок шестигранной игральной кости, на которой с равной вероятностью может выпасть одно из чисел 1, 2, 3, 4, 5 или 6. Следовательно, математическое ожидание одного броска равно

${\frac {1+2+3+4+5+6}{6}}=3{,}5.$

Согласно закону больших чисел, при большом количестве бросков их среднее значение, вероятно, будет близким к 3,5, при этом точность будет возрастать по мере увеличения числа бросков.

Из закона больших чисел следует, что эмпирическая вероятность успеха в серии испытаний Бернулли сходится к теоретической вероятности. Для случайной величины Бернулли математическое ожидание представляет собой теоретическую вероятность успеха, а среднее значение $n$ таких переменных (если они независимы и одинаково распределены) является относительной частотой.

Например, бросок правильной монеты — это испытание Бернулли. При одном броске теоретическая вероятность выпадения «орла» равна $1/2$. Поэтому, согласно закону больших чисел, доля «орлов» при большом количестве испытаний «должна быть» примерно $1/2$. В частности, доля «орлов» после $n$ бросков сходится к $1/2$, при $n\to \infty$.

Хотя доля орлов (и решек) стремится к $1/2$, почти наверняка модуль разности количества орлов и решек станет большим, когда число бросков будет неограниченно возрастать. То есть при увеличении числа бросков вероятность того, что модуль разницы будет невелик, идёт к нулю, а отношение модуля разницы к общему числу бросков почти наверное стремится к нулю:

$|n_{\text{о}}-n_{\text{р}}|\not \to 0,\quad {\frac {|n_{\text{о}}-n_{\text{р}}|}{n}}\to 0.$

История

Итальянский математик Джероламо Кардано (1501—1576) был страстным любителем азартных игр. «Побочным продуктом» его любви к игре в кости стала книга «Об азартных играх» (итал. De Ludo alea, 1563), содержащая формулировку закона больших чисел. В ней Кардано заявил, что точность эмпирической статистики, как правило, улучшается с количеством испытаний.

В 1713 году Якоб Бернулли изложил правила подсчёта вероятности для сложных событий и дал первый вариант «закона больших чисел», разъясняющего, почему частота события в серии испытаний не меняется хаотично, а в некотором смысле стремится к своему предельному теоретическому значению (то есть вероятности).

Следует также отметить работы С. Д. Пуассона (1781—1840), доказавшего более общую, чем у Якоба Бернулли, форму закона больших чисел.

П. Л. Чебышёв получил общую формулировку закона больших чисел: если математические ожидания серии случайных величин и квадраты этих математических ожиданий ограничены в совокупности, то среднее арифметическое этих величин с ростом сходится по вероятности к среднему арифметическому для их математических ожиданий.

А. А. Марков доказал вариант закона больших чисел для некоторых распространённых типов зависимых величин.

В XX веке исследования Чебышёва и Маркова продолжили А. Я. Хинчин и А. Н. Колмогоров. Они показали, что если случайные величины не только независимы, но и одинаково распределены, то существование у них математического ожидания является необходимым и достаточным условием для применимости закона больших чисел.

Варианты

Рассмотрим последовательность независимых в совокупности случайных величин $X_{1},X_{2},\dots$, интегрируемых по Лебегу, которые имеют одинаковые распределения, следовательно, и одинаковые математические ожидания $\mathbb {E} (X_{1})=\mathbb {E} (X_{2})=\ldots =\mu$.

Обозначим через ${\overline {X}}_{n}$ среднее арифметическое рассматриваемых случайных величин:

${\overline {X}}_{n}={\frac {1}{n}}(X_{1}+\ldots +X_{n}).$

Оно сходится к математическому ожиданию:

${\overline {X}}_{n}\to \mu$ при $n\to \infty .$

Независимость в совокупности случайных величин может быть заменена попарной независимостью в обоих вариантах закона.

Ниже описаны два различных варианта закона больших чисел. Их называют усиленным законом больших чисел и слабым законом больших чисел. Разница между усиленной и слабой формой связана с выбором способа сходимости.

Слабый закон

Слабый закон больших чисел (теорема Бернулли, сформулирована Я. Бернулли, опубликована в 1713 году) гласит, что среднее значение выборки сходится по вероятности к математическому ожиданию:

${\overline {X}}_{n}\xrightarrow {P} \mu$ при $n\to \infty .$

То есть $\forall \varepsilon >0$ выполняется

$\lim _{n\to \infty }P{\big (}|{\overline {X}}_{n}-\mu |>\varepsilon {\big )}=0.$

Интерпретируя данный результат, получаем, что слабый закон утверждает, что для любых ненулевых указанных границ, независимо от того, насколько они малы, при достаточно большой выборке вероятность того, что среднее значение выборки будет близко к математическому ожиданию, очень высока в пределах этих границ.

Как говорилось ранее, слабый закон применим в случае независимых одинаково распределённых случайных величин, имеющих математическое ожидание. Однако он может применяться и в некоторых других случаях. Например, дисперсия может быть разной для каждой случайной величины в выборке, а математическое ожидание оставаться константой. Если дисперсии ограничены, то закон также применим, как показал Чебышёв ещё в 1867 году. Доказательство Чебышёва работает до тех пор, пока дисперсия среднего числа первых $n$ значений не стремится к нулю при $n\to \infty$.

Усиленный закон

Усиленный закон больших чисел утверждает, что при определённых условиях с вероятностью единица происходит неограниченное сближение средних арифметических последовательности случайных величин с некоторыми постоянными величинами.

Пусть $X_{1},X_{2},\dots$ — последовательность случайных величин и ${\overline {X}}_{n}={\frac {1}{n}}(X_{1}+\ldots +X_{n})$.

Говорят, что последовательность $X_{1},X_{2},\dots$ удовлетворяет усиленному закону больших чисел, если существует такая последовательность $\mu _{n}$, что вероятность соотношения: ${\overline {X}}_{n}-\mu _{n}\to 0$, при $n\to \infty$ равна 1.

Другая формулировка, равносильная предыдущей, такова: последовательность $X_{1},X_{2},\dots$ удовлетворяет усиленному закону больших чисел, если $\forall \varepsilon >0$ вероятность одновременного выполнения всех неравенств

$|{\overline {X}}_{n}-\mu _{n}|\leqslant \varepsilon ,$

$|{\overline {X}}_{n+1}-\mu _{n+1}|\leqslant \varepsilon ,$

$\dots$

стремится к 1 при $n\to \infty$.

Таким образом, здесь рассматривается поведение всей последовательности сумм в целом, в то время как в обычном законе больших чисел речь идёт лишь об отдельных суммах.

Если последовательность $X_{1},X_{2},\dots$ удовлетворяет усиленному закону больших чисел, то она удовлетворяет и обычному закону больших чисел с теми же самыми $\mu _{n}$, то есть $P{\big (}|{\bar {X}}_{n}-\mu _{n}|\leqslant \varepsilon {\big )}\to 1$, при $n\to \infty$, $\forall \varepsilon >0$.

Обратное может быть неверно. Например, если случайные величины $X_{1},X_{2},\dots$ независимы и принимают при $n\geqslant 16$ два значения $\pm {\sqrt {n/\ln \ln \ln n}}$ с вероятностью $1/2$ каждое, то для них выполняется обычный закон больших чисел с $\mu _{n}=0$, но ни при каких $\mu _{n}$ не выполняется усиленный закон больших чисел.

Теорема Колмогорова

В случае независимых слагаемых наиболее известными являются условия приложимости усиленного закона больших чисел, установленные А. Н. Колмогоровым: достаточное — для величин с конечными дисперсиями, и необходимое и достаточное — для одинаково распределённых величин (заключающееся в существовании математического ожидания величин $X_{i}$). Теорема Колмогорова для случайных величин с конечными дисперсиями утверждает, что из условия

$\sum \limits _{n=1}^{\infty }{\frac {D[X_{n}]}{n^{2}}}<\infty$

(1)

вытекает приложимость к последовательности $X_{1},X_{2},\dots$ усиленного закона больших чисел с $A_{n}=\mathbb {E} ({\overline {X}}_{n})$. В терминах дисперсий условие (1) оказывается наилучшим в том смысле, что для любой последовательности положительных чисел $b_{n}$ с расходящимся рядом $\sum b_{n}/n^{2}$ можно построить последовательность независимых случайных величин $X_{n}$ с $DX_{n}=b_{n}$, не удовлетворяющую усиленному закону больших чисел.

Различия между слабым законом и усиленным законом

Слабый закон утверждает, что для заданного большого $n$ среднее значение ${\overline {X}}_{n}$, вероятно, будет близко к $\mu$. Таким образом, $|{\overline {X}}_{n}-\mu |>\varepsilon$ может происходить бесконечно много раз, хотя и сколь угодно редко. (Для всех $n$ не обязательно выполняется $|{\overline {X}}_{n}-\mu |\neq 0$).

Усиленный закон показывает, что $|{\overline {X}}_{n}-\mu |>\varepsilon$ почти наверное не произойдёт. Это означает, что с вероятностью 1 мы имеем, что $\forall \varepsilon >0$ выполняется неравенство $|{\overline {X}}_{n}-\mu |<\varepsilon$ для достаточно больших $n$.

Ниже приведены три примера симметричных распределений, в каждом примере математического ожидания эти распределения не имеют, усиленный закон больших чисел (сходимость почти всюду) не имеет места, но слабый закон выполнен: среднее случайных величин сходится по вероятности к константе, центру симметрии их распределения.

1. Пусть $x$ — экспоненциально распределённая случайная величина с параметром 1. Случайная величина ${\frac {\sin(x)e^{x}}{x}}$ не имеет математического ожидания, задаваемого интегралом Лебега, но используя условную сходимость и интерпретацию интеграла как интеграла Дирихле, являющегося несобственным интегралом Римана, можно сказать:

   $\mathbb {E} \left({\frac {\sin(x)e^{x}}{x}}\right)=\int _{0}^{\infty }{\frac {\sin(x)e^{x}}{x}}e^{-x}\,dx={\frac {\pi }{2}}.$

2. Пусть $x$ — геометрическое распределение с вероятностью $0{,}5$. Случайная величина ${\frac {2^{x}(-1)^{x}}{x}}$не имеет математического ожидания в обычном смысле, поскольку бесконечный ряд не является абсолютно сходящимся, но используя условную сходимость можно сказать:

   $\mathbb {E} \left({\frac {2^{x}(-1)^{x}}{x}}\right)=\sum _{1}^{\infty }{\frac {2^{x}(-1)^{x}}{x}}2^{-x}=-\ln(2).$

3. Если функция распределения случайной величины равна

   $1-F(x)={\frac {e}{2x\ln(x)}},\quad x\geqslant e,$

   $F(x)={\frac {e}{-2x\ln(-x)}},\quad x\leqslant -e,$

   то она не имеет математического ожидания, но слабый закон выполняется.

Равномерный закон больших чисел

Пусть $f(x,\theta )$ — некоторая функция, которая определена и непрерывна по переменной $\theta \in \Theta$. Тогда для любого фиксированного $\theta$ последовательность $\{f(X_{1},\theta ),f(X_{2},\theta ),\dots \}$ будет последовательностью независимых и одинаково распределённых случайных величин, такой, что выборочное среднее этой последовательности сходится по вероятности к $\mathbb {E} [f(X,\theta )]$.

Равномерный закон больших чисел описывает условия, при которых сходимость равномерна по $\theta$.

Если:

1. $\Theta$ компактно,
2. $f(x,\theta )$ непрерывна при каждом $\theta \in \Theta$ для почти всех $x$ и измеримой функции от $x$ в каждом $\theta$,
3. существует доминирующая функция $d(x)$ такая, что $\mathbb {E} [d(X)]<\infty$ и $\|f(x,\theta )\|\leqslant d(x)$ для всех $\theta \in \Theta$,

тогда $\mathbb {E} [f(X,\theta )]$ непрерывна в $\theta$ и

$\sup _{\theta \in \Theta }\left\|{\frac {1}{n}}\sum _{i=1}^{n}f(X_{i},\theta )-\mathbb {E} [f(X,\theta )]\right\|\xrightarrow {\text{п. н.}} 0.$

Борелевский закон больших чисел

Борелевский закон больших чисел, названный в честь Эмиля Бореля, гласит, что если эксперимент повторяется много раз независимо при одинаковых условиях, то доля раз, когда любое указанное событие происходит, приблизительно равна вероятности появления события в каком-либо конкретном испытании; чем больше число повторений, тем лучше приближение. Точнее, если $E$ обозначает событие, о котором идёт речь, $p$ — вероятность его появления, а $N_{n}(E)$ — число раз, когда $E$ встречается в первых $n$ испытаниях, тогда с вероятностью 1

${\frac {N_{n}(E)}{n}}\to p,\quad n\to \infty .$

Неравенство Чебышёва

Пусть $X$ — случайная величина с конечным математическим ожиданием $\mu$ и конечной ненулевой дисперсией $\sigma ^{2}$. Тогда для любого действительного числа $k>0$ выполняется

$P{\big (}|X-\mu |\geqslant k\sigma {\big )}\leqslant {\frac {1}{k^{2}}}.$

Доказательство слабого закона

Рассмотрим бесконечную последовательность $X_{1},X_{2},\dots$ независимых и одинаково распределённых случайных величин с конечным математическим ожиданием $\mathbb {E} (X_{1})=\mathbb {E} (X_{2})=\ldots =\mu <\infty$. Нас интересует сходимость по вероятности

${\overline {X}}_{n}={\frac {1}{n}}(X_{1}+\ldots +X_{n}).$

Теорема

${\overline {X}}_{n}\xrightarrow {P} \mu$ при $n\to \infty .$

Доказательство с использованием неравенства Чебышёва, предполагающего конечную дисперсию

Предположение о конечной дисперсии $D(X_{1})=D(X_{2})=\ldots =\sigma ^{2}<\infty$ не является обязательным. Большая или бесконечная дисперсия замедляет сходимость, но ЗБЧ выполняется в любом случае.

Это доказательство использует предположение о конечной дисперсии $\operatorname {D} (X_{i})=\sigma ^{2}$ (для всех $i$). Независимость случайных величин не предполагает корреляции между ними, мы имеем

$\operatorname {D} ({\overline {X}}_{n})=\operatorname {D} {\big (}{\tfrac {1}{n}}(X_{1}+\ldots +X_{n}){\big )}={\frac {1}{n^{2}}}\operatorname {D} (X_{1}+\ldots +X_{n})={\frac {n\sigma ^{2}}{n^{2}}}={\frac {\sigma ^{2}}{n}}.$

Математическое ожидание последовательности $\mu$ представляет собой среднее значение выборочного среднего:

$\mathbb {E} ({\overline {X}}_{n})=\mu .$

Используя неравенство Чебышёва для ${\overline {X}}_{n}$, получаем

$\operatorname {P} {\big (}|{\overline {X}}_{n}-\mu |\geqslant \varepsilon {\big )}\leqslant {\frac {\sigma ^{2}}{n\varepsilon ^{2}}}.$

Это неравенство используем для получения следующего:

$\operatorname {P} {\big (}|{\overline {X}}_{n}-\mu |<\varepsilon {\big )}=1-\operatorname {P} {\big (}|{\overline {X}}_{n}-\mu |\geqslant \varepsilon {\big )}\geqslant 1-{\frac {\sigma ^{2}}{n\varepsilon ^{2}}}.$

При $n\to \infty$ выражение стремится к 1.

Теперь по определению сходимости по вероятности мы получим:

${\overline {X}}_{n}\xrightarrow {P} \mu$ при $n\to \infty$.

Доказательство с использованием сходимости характеристических функций

По теореме Тейлора для комплексных функций, характеристическая функция любой случайной величины $X$ с конечным средним $\mu$ может быть записана как

$\varphi _{X}(t)=1+it\mu +o(t),\quad t\to 0.$

Все $X_{1},X_{2},\dots$ имеют одну и ту же характеристическую функцию, обозначим её как $\varphi _{X}$.

Среди основных свойств характеристических функций выделим два свойства:

$\varphi _{{\frac {1}{n}}X}(t)=\varphi _{X}{\big (}{\tfrac {t}{n}}{\big )},$

$\varphi _{X+Y}(t)=\varphi _{X}(t)\,\varphi _{Y}(t),$

где $X$ и $Y$ независимы.

Эти правила могут быть использованы для вычисления характеристической функции ${\overline {X}}_{n}$ в терминах $\varphi _{X}$:

$\varphi _{{\overline {X}}_{n}}(t)=\left[\varphi _{X}\left({\frac {t}{n}}\right)\right]^{n}=\left[1+i\mu {\frac {t}{n}}+o\left({\frac {t}{n}}\right)\right]^{n}\to e^{it\mu }$ при $n\to \infty .$

Предел $e^{it\mu }$ является характеристической функцией константы $\mu$ и, следовательно, по теореме непрерывности Леви, ${\overline {X}}_{n}$ сходится по распределению к $\mu$:

${\overline {X}}_{n}\xrightarrow {\mathcal {D}} \mu$ при $n\to \infty .$

Поскольку $\mu$ — константа, то отсюда следует, что сходимость по распределению к $\mu$ и сходимость по вероятности к $\mu$ эквивалентны. Поэтому

${\overline {X}}_{n}\xrightarrow {\mathcal {P}} \mu$ при $n\to \infty .$

Это показывает, что среднее значение выборки по вероятности сходится к производной характеристической функции в начале координат, если она существует.

См. также

• Закон малых чисел
• Закон повторного логарифма
• Теорема Колмогорова о трёх рядах
• Теорема о бесконечных обезьянах
• Центральная предельная теорема

Литература

• Чистяков В. П. Курс теории вероятностей. — М. : Наука, 1982.
• Ширяев А. Н. Вероятность. — М. : Наука, 1989.
• Пасхавер И. С. Закон больших чисел и статистические закономерности. — М. : Статистика, 1974.
• Теорема Бернулли : [арх. 3 октября 2022] / В. И. Битюцков // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.