Снарк «Цветок»

В теории графов снарки «Цветы» образуют бесконечное семейство снарков, введённых Айзексом Руфусом в 1975 году.

Снарки «Цветок» J3, J5 и J7.
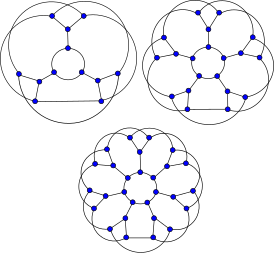Вершин	4n
Рёбер	6n
Обхват	3 для n=3 5 для n=5 6 для n≥7
Хроматическое число	3
Хроматический индекс	4
Свойства	снарк для n≥5
Медиафайлы на Викискладе

Снарк «Цветок» J5
Вершин	20
Рёбер	30
Обхват	5
Хроматическое число	3
Хроматический индекс	4
Свойства	снарк гипогамильтонов
Медиафайлы на Викискладе

Как и все снарки, цветы являются связными кубическими графами без мостов с хроматическим индексом 4. Они не планарны и не гамильтоновы.

Построение

Цветок J_n можно построить следующим процессом:

• Образуем n копий звезды с 4 вершинами. Обозначим центр каждой звезды через A_i, а внешние вершины — через B_i, C_i и D_i. Результатом будет несвязный граф с 4n вершинами и 3n рёбрами (A_i-B_i, A_i-C_i и A_i-D_i для 1≤i≤n).
• Образуем цикл длины n (B₁... B_n). Это добавит n рёбер.
• Образуем цикл длины 2n (C₁... C_nD₁... D_n). Это добавит ещё 2n рёбер.

По построению цветок J_n является кубическим графом с 4n вершинами и 6n рёбрами. Чтобы получить необходимые свойства, n должен быть нечётным.

Специальные случаи

Название «цветок» иногда используется для J₅, снарка с 20 вершинами и 30 рёбрами. Это один из 6 снарков с 20 вершинами (последовательность A130315 в OEIS). Цветок J₅ является гипогамильтоновым.

J₃ является тривиальным вариантом графа Петерсена, полученный путём применения преобразования треугольник-звезда к графу Петерсена, а затем заменой одной из вершин треугольником. Этот граф известен также как граф Титце. Чтобы избежать тривиальных случаев, обычно графы с обхватом меньше 5 не рассматриваются как снарки. Если следовать этим ограничениям, J₃ снарком не является.

Галерея

• 
  хроматическое число цветка J₅ равно 3
• 
  хроматический индекс цветка J₅ равен 4.
• 
  Первоначальное представление цветка J₅.