Свободное произведение

Свободным произведением групп называется группа, порождённая элементами этих двух групп, без каких-либо дополнительных соотношений.

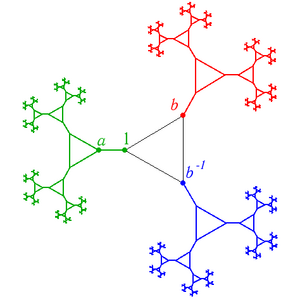
Свободное произведение $G_{1}$ и $G_{2}$ обычно обозначается $G_{1}*G_{2}$ .

Определения

Если группы заданы через порождающие и соотношения $G_{1}=\langle S_{1}|R_{1}\rangle$ , $G_{2}=\langle S_{2}|R_{2}\rangle$ то
$G_{1}*G_{2}=\langle S_{1}\cup S_{2}|R_{1}\cup R_{2}\rangle$
- Это определение также допускает естественное обобщение на случай свободного произведения любого числа групп.

Свободное произведение $G_{1}*G_{2}$ можно также определить как расслоенное копроизведение $G_{1}\amalg _{\{e\}}G_{2}$ для тривиальной группы $\{e\}$ в категории групп.

Свободное произведение $\mathbb {Z} _{2}*\mathbb {Z} _{2}$ изоморфно бесконечной группе диэдра $D_{\infty }$ .
Свободное произведение $\mathbb {Z} _{2}*\mathbb {Z} _{3}$ изоморфно проективной группе $PSL(2,\mathbb {Z} )$ .
Свободное произведение $n$ копий $\mathbb {Z}$ — свободная группа с $n$ образующими.
Теорема Зейферта — ван Кампена в частности утверждает, что если $X$ — топологическое пространство, и $V,U\subset X$ — два связных открытых множества таких, что пересечение $W=V\cap U$ односвязно, и $X=V\cup U$ , то фундаментальная группа $X$ есть свободное произведение фундаментальных групп $V$ и $U$ ; то есть
$\pi _{1}X=\pi _{1}V*\pi _{1}U.$