Ромбоикосододекаэдр

Ромбоикосододека́эдр — полуправильный многогранник (архимедово тело) с 62 гранями, составленный из 20 правильных треугольников, 30 квадратов и 12 правильных пятиугольников.

Ромбоикосододекаэдр
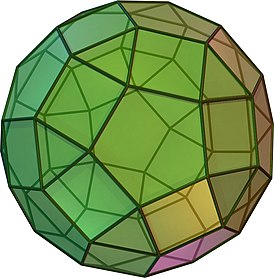(вращающаяся модель, 3D-модель)
Тип	архимедово тело
Свойства	выпуклый, изогональный
Комбинаторика
Элементы	62 грани 120 рёбер 60 вершин Χ = 2
Грани	20 треугольников 30 квадратов 12 пятиугольников
Конфигурация вершины	3.4.5.4
Двойственный многогранник	дельтоидальный гексеконтаэдр
Развёртка
Классификация
Обозначения	eD, aaD
Символ Шлефли	rr{5,3}
Группа симметрии	Ih (икосаэдрическая)
Медиафайлы на Викискладе

В каждой из его 60 одинаковых вершин сходятся одна пятиугольная грань, две квадратных и одна треугольная. Телесный угол при вершине равен $2\pi -\arccos {\frac {5-4{\sqrt {5}}}{15}}\approx 1{,}42\pi .$

Ромбоикосододекаэдр имеет 120 рёбер равной длины. При 60 рёбрах (между треугольной и квадратной гранями) двугранные углы равны $\arccos \left(-{\frac {{\sqrt {15}}+{\sqrt {3}}}{6}}\right)\approx 159{,}09^{\circ };$ при 60 рёбрах (между квадратной и пятиугольной гранями) $\arccos \left(-{\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right)\approx 148{,}28^{\circ }.$

Ромбоикосододекаэдр можно представить либо как додекаэдр, усечённый по вершинам и рёбрам (при этом треугольники соответствуют вершинам додекаэдра, а квадраты — рёбрам), либо как икосаэдр, усечённый таким же образом (при этом пятиугольники соответствуют вершинам икосаэдра, а квадраты — рёбрам), либо же как усечённый икосододекаэдр.

Фрагмент титульного листа «Геометрии» Августина Хиршфогеля (1543)

В координатах

Ромбоикосододекаэдр с длиной ребра $2$ можно расположить в декартовой системе координат так, чтобы координаты его вершин были всевозможными циклическими перестановками наборов чисел

• $(\pm 1;\;\pm 1;\;\pm (2\Phi +1)),$
• $(\pm (\Phi +1);\;\pm \Phi ;\;\pm 2\Phi ),$
• $(\pm (\Phi +2);\;0;\;\pm (\Phi +1)),$

где $\Phi ={\frac {1+{\sqrt {5}}}{2}}$ — отношение золотого сечения.

Начало координат $(0;\;0;\;0)$ будет при этом центром симметрии многогранника, а также центром его описанной и полувписанной сфер.

Метрические характеристики

Для удобства представления грани ромбоикосододекаэдра можно мысленно разделить на пять «поясов».

Пара каменных ромбоикосододекаэдров возле Капитолия штата Пенсильвания (установлены в 1928 году).

Если ромбоикосододекаэдр имеет ребро длины $a$, его площадь поверхности и объём выражаются как

$S=\left(30+5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}\approx 59{,}3059828a^{2},$

$V={\frac {1}{3}}\left(60+29{\sqrt {5}}\right)a^{3}\approx 41{,}6153238a^{3}.$

Радиус описанной сферы (проходящей через все вершины многогранника) при этом будет равен

$R={\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}\;a\approx 2{,}2329505a;$

радиус полувписанной сферы (касающейся всех рёбер в их серединах) —

$\rho ={\frac {1}{2}}{\sqrt {10+4{\sqrt {5}}}}\;a\approx 2{,}1762509a.$

Вписать в ромбоикосододекаэдр сферу — так, чтобы она касалась всех граней, — невозможно. Радиус наибольшей сферы, которую можно поместить внутри ромбоикосододекаэдра с ребром $a$ (она будет касаться только всех пятиугольных граней в их центрах), равен

$r_{5}={\frac {3}{2}}{\sqrt {1+{\frac {2}{\sqrt {5}}}}}\;a\approx 2{,}0645729a.$

Расстояния от центра многогранника до квадратных и треугольных граней превосходят $r_{5}$ и равны соответственно

$r_{4}={\frac {1}{2}}\left(2+{\sqrt {5}}\right)a\approx 2{,}1180340a,$

$r_{3}=\left({\frac {\sqrt {3}}{2}}+{\sqrt {\frac {5}{3}}}\right)a\approx 2{,}1570199a.$

В культуре

Соединители в Zometool

В наборах для моделирования пространственных фигур Zometool в качестве соединителей используются рёберные каркасы ромбоикосододекаэдра.

Литература

• М. Веннинджер. Модели многогранников. — Мир, 1974.
• Многоугольники и многогранники // Энциклопедия элементарной математики. Книга четвёртая. Геометрия / Под ред. П. С. Александрова, А. И. Маркушевича, А. Я. Хинчина. — М.: Государственное издательство физико-математической литературы, 1963. — С. 382—447.
• Л. А. Люстерник. Выпуклые фигуры и многогранники. — М.: Государственное издательство технико-теоретической литературы, 1956.

Ссылки

• Weisstein, Eric W. Ромбоикосододекаэдр (англ.) на сайте Wolfram MathWorld.