Пра́вильный семнадцатиуго́льник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Среди других правильных многоугольников с больши́м (больше пяти) простым числом сторон интересен тем, что его можно построить при помощи циркуля и линейки (так, семи-, одиннадцати- и тринадцатиугольники построить циркулем и линейкой нельзя).
| Семнадцатиугольник | |
|---|---|
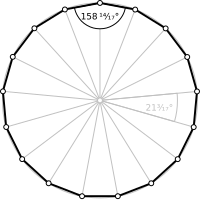 Правильный семнадцатиугольник | |
| Тип | Правильный многоугольник |
| Рёбра | 17 |
| Символ Шлефли | {17} |
| Диаграмма Коксетера — Дынкина |
|
| Вид симметрии | Диэдрическая группа (D18) порядок 2×18 |
| Внутренний угол | ≈158.82° |
| Свойства | |
| выпуклый, вписанный, равносторонний, равноугольный[англ.], изотоксальный | |
Свойства
правитьЦентральный угол α равен .
Отношение длины стороны к радиусу описанной окружности составляет
Правильный семнадцатиугольник можно построить при помощи циркуля и линейки, что было доказано Гауссом в монографии «Арифметические исследования» (1796 год). Им же найдено значение косинуса центрального угла семнадцатиугольника:
В этой же работе Гаусс доказал, что если нечётные простые делители числа n являются различными простыми Ферма (числа Ферма), то есть простыми числами вида то правильный n-угольник может быть построен с помощью циркуля и линейки (см. Теорема Гаусса — Ванцеля).
Факты
править- Гаусс был настолько воодушевлён своим открытием, что в конце жизни завещал, чтобы правильный семнадцатиугольник высекли на его могиле. Скульптор отказался это сделать, утверждая, что построение будет настолько сложным, что результат нельзя будет отличить от окружности.
- В 1893 году Герберт Уильям Ричмонд[англ.] опубликовал явное описание построения правильного семнадцатиугольника в 64 шагах. Ниже приводится это построение.
Построение
правитьТочное построение
править- Проводим большую окружность k₁ (будущую описанную окружность семнадцатиугольника) с центром O.
- Проводим её диаметр AB.
- Строим к нему перпендикуляр m, пересекающий k₁ в точках C и D.
- Отмечаем точку E — середину DO.
- Посередине EO отмечаем точку F и проводим отрезок FA.
- Строим биссектрису w₁ угла ∠OFA.
- Строим w₂ — биссектрису угла между m и w₁, которая пересекает AB в точке G.
- Восстанавливаем s — перпендикуляр к w₂ из точки F.
- Строим w₃ — биссектрису угла между s и w₂. Она пересекает AB в точке H.
- Строим окружность Фалеса (k₂) на диаметре HA с центром в точке M. Она пересекается с CD в точках J и K.
- Проводим окружность k₃ с центром G через точки J и K. Она пересекается с AB в точках L и N. Здесь важно не перепутать N с M, они расположены очень близко.
- Строим касательную к k₃ через N.
Точки пересечения этой касательной с исходной окружностью k₁ — это точки P₃ и P₁₄ искомого семнадцатиугольника. Если принять середину получившейся дуги за P₀ и отложить дугу P₀P₁₄ по окружности три раза, все вершины семнадцатиугольника будут построены.
Примерное построение
правитьСледующее построение хоть и приблизительно, но гораздо более удобно.
- Ставим на плоскости точку M, строим вокруг неё окружность k и проводим её диаметр AB;
- Делим пополам радиус AM три раза по очереди по направлению к центру (точки C, D и E).
- Делим пополам отрезок EB (точка F).
- строим перпендикуляр к AB в точке F.
- Вкратце: строим перпендикуляр к диаметру на расстоянии 9/16 диаметра от B.
Точки пересечения последнего перпендикуляра с окружностью являются хорошим приближением для точек P₃ и P₁₄.
При этом построении получается относительная ошибка в 0,83%. Углы и стороны получаются таким образом немного больше, чем нужно. При радиусе 332,4 мм сторона получается длиннее на 1 мм.
Анимированное построение Эрхингера
правитьЗвёздчатые формы
правитьУ правильного семнадцатиугольника существуют 7 правильных звёздчатых форм.
-
{17/2}
-
{17/3}
-
{17/4}
-
{17/5}
-
{17/6}
-
{17/7}
-
{17/8}
См. также
правитьСсылки
править- Karin Reich. Die Entdeckung und frühe Rezeption der Konstruierbarkeit des regelmäßigen 17-Ecks und dessen geometrische Konstruktion durch Johannes Erchinger (1825). // В кн.: Mathesis, Festschrift zum siebzigsten Geburtstag von Matthias Schramm. Hrsg. von Rüdiger Thiele, Berlin, Diepholz 2000, стр. 101—118.
- Weisstein, Eric W. Семнадцатиугольник (англ.) на сайте Wolfram MathWorld.