Полуикосаэдр
Полуикосаэдр — абстрактный правильный многогранник, содержащий половину граней правильного икосаэдра. Он может быть реализован как проективный многогранник[англ.] (мозаика проективной плоскости 10 треугольниками), который можно представить себе путём построения проективной плоскости как полусферы, противоположные точки которой вдоль границы соединены и делят полусферу на три равные части.
| Полуикосаэдр | ||
|---|---|---|
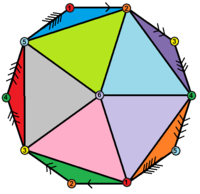 Десятиугольная диаграмма Шлегеля | ||
| Тип |
Абстрактный правильный многогранник проективный многогранник[англ.] |
|
| Свойства |
неориентированный[англ.] эйлерова характеристика = 1 |
|
| Комбинаторика | ||
| Элементы |
|
|
| Грани | 10 треугольников | |
| Конфигурация вершины | 3.3.3.3.3 | |
| Двойственный многогранник | полудодекаэдр | |
| Классификация | ||
| Символ Шлефли | {3,5}/2 or {3,5}5 | |
| Группа симметрии | A5, порядок 60 | |
Геометрия
правитьПолуикосаэдр имеет 10 треугольных граней, 15 рёбер и 6 вершин.
Он также связан с невыпуклым однородным многогранником, тетрагемигексаэдром, который топологически идентичен полуикосаэдру, если 3 его квадратные грани разделить на треугольники.
Графы
правитьМногогранник можно представить симметричным относительно граней и вершин диаграммой Шлегеля:
| Гранецентрированная диаграмма |
|---|
Полный граф K6
правитьМногогранник имеет те же вершины и рёбра, что и пятимерный гексатерон, имеющий полный набор рёбер, но содержит только половину (20) граней.
С точки зрения теории графов это вложение графа (полный граф с 6 вершинами) в проективную плоскость. Для этого вложения двойственным графом будет граф Петерсена (см. полудодекаэдр).
См. также
править- 11-ячейник – абстрактный правильный четырёхмерный многогранник, построенный из 11 hemi-icosahedra.
- полудодекаэдр
- Полукуб[англ.]
- Полуоктаэдр[англ.]
Литература
править- Peter McMullen, Egon Schulte. 6C. Projective Regular Polytopes // Abstract Regular Polytopes. — Cambridge University Press, December 2002. — P. 162–165. — ISBN 0-521-81496-0.
Ссылки
правитьДля улучшения этой статьи желательно:
|