Орицикл (греч. ὅρος + κύκλος — «граница + круг»), предельная линия ― линия на плоскости Лобачевского, ортогональная к некоторому семейству параллельных прямых.
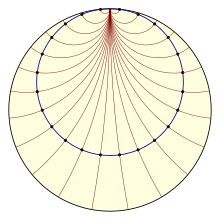
Орицикл может быть определён как предел семейства окружностей с общей касательной, проходящих через фиксированную точку и лежащих по одну сторону от этой касательной, образующийся при стремлении радиуса этих окружностей к бесконечности. Неформально его можно рассматривать как «окружность бесконечно большого радиуса с бесконечно удалённым центром».
Все орициклы конгруэнтны между собой, кривизна орицикла постоянна.
В модели Пуанкаре орицикл ― окружность, касающаяся изнутри абсолюта.
См. также
править- Гиперцикл — это кривая, точки которой лежат на фиксированном расстоянии до прямой.