Орисфера

Орисфера ― поверхность пространства Лобачевского, ортогональная к прямым, параллельным в некотором направлении.

Орицикл ― аналог орисферы на плоскости Лобачевского, изображён в конформной модели на диске.

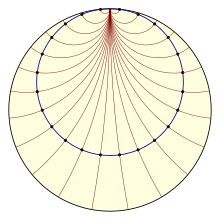
Орисферу можно рассматривать как сферу с бесконечно удаленным центром, точнее она является пределом сфер проходящих через фиксированную точку и центром стремящимся к бесконечности вдоль фиксированного луча. Эквивалентно, орисфера это поверхность уровня функции Буземана, построенной по этому лучу.

Свойства

• Орисфера с индуцированной внутренней метрикой изометрична евклидовой плоскости, при этом движения плоскости продолжаются до движений пространства Лобачевского, переводящих орисферу в себя.
  • Этот факт был замечен уже Лобачевским. По сути он даёт модель евклидовой плоскости в геометрии Лобачевского и может быть использован при доказательстве непротиворечивости евклидовой геометрии в предположении непротиворечивости геометрии Лобачевского.

Литература

• Клейн Ф. «Неевклидова геометрия», М.-Л., ОНТИ, 1936, 356 с.
• Иовлев Н. Н. «Введение в элементарную геометрию и тригонометрию Лобачевского», М. -Л., Гиз, 1930 г., 67 с.

См. также

• Орицикл
• Паракомпактные замощения пространства Лобачевского