Модулярная решётка
Модулярная решётка (дедекиндова решётка) — решётка, в которой каждая пара элементов модулярна, то есть справедлив закон модулярности — квазитождество:
- .
Важнейший пример модулярной решётки — решётка подпространств векторного пространства; также модулярны решётка нормальных подгрупп группы, решётка идеалов кольца.
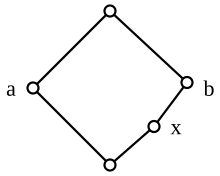
Любая дистрибутивная решётка является модулярной, обратное неверно: ромб (диамант) — пример модулярной решётки, которая не является дистрибутивной.
Наименьшая немодулярная решётка — пятиэлементный пентагон , любая немодулярная решётка содержит его в качестве подрешётки.
В модулярных решётках справедлива теорема об изоморфизмах интервалов: для любых двух элементов модулярной решётки и интервалы и изоморфны, прямое отображение: , обратное — .
Немодулярная решётка может содержать элементы, удовлетворяющие закону модулярности. Элемент называется левомодулярным, если для любого элемента пара модулярна.
Элемент называется правомодулярным, если для любого элемента пара модулярна.
Закон модулярности и некоторые его следствия впервые установлены Рихардом Дедекиндом в 1894 году.
Литература
править- Дедекиндова решётка — статья из Математической энциклопедии. Л. А. Скорняков
- Салий В. Н., Скорняков Л. А. . Глава V. Решётки // Общая алгебра / Под общ. ред. Л. А. Скорнякова. — М.: Наука, 1991. — Т. 2. — С. 192—294. — 480 с. — (Справочная математическая библиотека). — 25 000 экз. — ISBN 5-9221-0400-4.
- Г. Гретцер. IV. Модулярные решётки // Общая теория решёток = General Lattice Theory / под редакцией Д. М. Смирнова. — М.: Мир, 1981. — С. 211—224. — 456 с.
- Биркгоф Г. Теория решёток. — М.: Наука, 1984. — 568 с.
Это заготовка статьи по математике. Помогите Википедии, дополнив её. |





![{\displaystyle [a\wedge b,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b0393d6f6c22dfa89d7d560022398535b72408c)
![{\displaystyle [a,a\vee b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/879c2a825e065f5181818beba0ce853bb34163de)


