Мир тесен (граф)

Граф «Мир те́сен» (ма́ленький мир) — разновидность графа, который имеет следующее свойство: если взять две произвольные вершины a и b, то они с большой вероятностью не являются смежными, однако одна достижима из другой посредством небольшого количества переходов через другие вершины. А именно, граф «Мир тесен» определяется как сеть, в которой типичное расстояние L между двумя произвольно выбранными вершинами (количество шагов, необходимых, чтобы достичь одну из другой) растёт пропорционально логарифму от числа вершин N в сети, таким образом:

Пример графа «Мир тесен», выделены вершины — хабы.
Средняя степень вершины = 3,833
Средняя длина кратчайшего пути = 1.803.
Коэффициент кластеризации = 0.522

Случайный граф
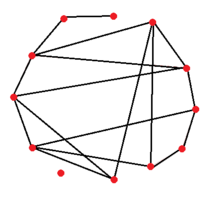
Средняя степень вершины = 2,833
Средняя длина кратчайшего пути = 2.109.
Коэффициент кластеризации = 0.167

$L\propto \log N$,

но при этом глобальный коэффициент кластеризации не является малым.

В контексте социальной сети это приводит к феномену «Мир тесен», то есть незнакомых людей связывает небольшое количество промежуточных знакомых. Много реально существующих графов хорошо моделируются через графы «Мир тесен». Социальные сети, связность сети Интернет, вики-сайты, такие, как Википедия, и генные сети проявляют свойства графа «Мир тесен». Дункан Уоттс и Стивен Строгац в 1998 году идентифицировали определённую категорию графов «Мир тесен» как класс случайных графов. Они отметили, что такие графы могут быть классифицированы в соответствии с двумя независимыми структурными особенностями, а именно коэффициент кластеризации и расстояние от одной вершины до другой в среднем (также известное как длина кратчайшего пути в среднем). Совершенно случайные графы, построенные в соответствии с моделью Эрдёша — Реньи, имеют малую длину кратчайшего пути в среднем (она растёт как логарифм от количества вершин в графе) и маленький коэффициент кластеризации. Уоттс и Строгац выяснили, что большинство реально существующих сетей имеют малую длину кратчайшего пути в среднем, но коэффициент кластеризации в них существенно выше, чем ожидается при случайном выборе. После этого Уоттс и Строгац предложили новую модель графа, в настоящее время называемую модель Уоттса — Строгаца, для которой характерны (i) малая длина кратчайшего пути в среднем, и (ii) большой коэффициент кластеризации. Пересечение в модели Уоттса и Строгаца между «большим миром» (таким, как решётчатый граф) и маленьким миром было впервые описано Бартелми и Амарал в 1999. За этой работой последовало большое количество исследований.

Свойства графа «Мир тесен»

Графы «Мир тесен» имеют тенденцию содержать в себе клики и почти-клики, под которыми понимают подсети, имеющие связи почти между всеми вершинами в них. Это следует из определения такого свойства графа, как высокий коэффициент кластеризации. Во-вторых, большинство пар вершин будут соединены хотя бы одним коротким путём. Более строго: расстояние от одной вершины до другой в среднем (также известное как длина кратчайшего пути в среднем) относительно мало. Длина кратчайшего пути в среднем высчитывается по следующей формуле:

$L={\frac {1}{N(N-1)}}\sum _{i,j\in N,i\neq j}d_{ij}$

$d_{ij}$ — расстояние от вершины $i$ до вершины $j$

$N$ — количество вершин в графе

Некоторые другие особенности, которые будут описаны далее, часто присутствуют в графах «Мир тесен». Обычно в таких графах много хабов — вершин, степень которых значительно (во много раз) больше чем степени большинства вершин графа. Именно эти хабы уменьшают средний кратчайший путь графа. Типичным примером графа «Мир тесен» является сеть авиарейсов с узлами-аэропортами. Между любыми двумя городами в мире потребуется, вероятно, не больше трёх перелётов из-за того, что большинство авиарейсов проходят через узловые аэропорты.

Для анализа этого свойства (а именно, наличия хабов) учитывают долю вершин в сети, которые имеют большую степень. Сети с бо́льшим количеством хабов, чем ожидается, будут иметь бо́льшую долю вершин с высокой степенью, и очень много вершин с малыми степенями. Следовательно распределение степеней вершин графа будет «распределением тяжёлого хвоста». Графы очень разной топологии классифицируются как графы «Мир тесен», если выполняются указанные выше два условия.

Принадлежность к классу графов «Мир тесен» оценивается сравнением кластеризации и длины путей данной сети с соответствующими параметрами эквивалентной случайной сети с такой же средней степенью вершин . Другой метод оценивания принадлежности сети к классу графов «Мир тесен» использует исходное определение графа «Мир тесен», сравнивая степень кластеризации данной сети со степенью кластеризации эквивалентного графа-решётки и длину среднего пути с длиной среднего пути в произвольном графе. Мера принадлежности графа к классу «Мир тесен» ($\omega$) определяется, как

$\omega ={\tfrac {L_{r}}{L}}-{\tfrac {C}{C_{l}}}$

$L$ — средняя длина кратчайшего пути в рассматриваемом графе

$C$ — степень кластеризации рассматриваемого графа

$L_{r}$ — длина кратчайшего пути в среднем в случайном графе

$C_{l}$ — степень кластеризации графа-решётки

Р. Коуэн и Шломо Хавлин показали аналитически, что безмасштабные сети — ультра-малые миры. В этом случае, из-за хабов, кратчайшие пути становятся существенно короче и масштабируются как

$L\propto \log \log N$

Примеры графов «мир тесен»

Свойства графа «мир тесен» были обнаружены во многих объектах реального мира, включая карты дорог, пищевые цепочки, электрические сети, сети протекания метаболизма (metabolite processing networks), нейронные сети, сети избирателей, граф телефонных звонков и сети социального влияния.

Белок-белковые взаимодействия имеют такое свойство графа «Мир тесен», как соответствие степенному закону распределения.

Аналогично, свойствами графа «Мир тесен» обладает регуляция транскрипции, в которой вершинам соответствуют гены, причём они связаны, если один ген имеет вверх- или вниз-регулирующее генетическое влияние на другой.

Надёжность сети

Некоторыми исследователями (например, Barabási ) было высказано предположение, что распространённость графов «Мир тесен» в биологических системах может отражать эволюционное преимущество такой топологии. Поводом к такому предположению стала гипотеза, что графы «Мир тесен» более устойчивы при различных внешних воздействиях по сравнению с другими топологиями сети. Если бы эта гипотеза была верна, то это обеспечило бы преимущество биологическим системам, которые являются субъектами мутаций и вирусных инфекций.

В графах «Мир тесен» со степенным законом распределения степеней вершин удаление случайной вершины редко служит причиной существенного увеличения кратчайшего пути в среднем (или существенного уменьшения коэффициента кластеризации). Это следует из того факта, что большинство кратчайших путей проходят через хаб, и если периферическая вершина удаляется, маловероятно, что она вмешается в прохождение между другими периферийными вершинами. Поскольку доля периферийных вершин в графе «Мир тесен» существенно выше, чем доля хабов, вероятность удаления важной вершины крайне мала. Например, если маленький аэропорт в Петрозаводске перестанет функционировать, то это не увеличит среднее количество полётов, которые требуются пассажирам, чтобы добраться до точки назначения. Тем не менее, если случайное удаление попадает в хаб, длина кратчайшего пути в среднем может вырасти весьма существенно. Это можно увидеть ежегодно, когда какой-либо аэропорт, располагающийся в северных штатах в США, такой, как Чикагский аэропорт О’Хара (штат Иллинойс) заносит снегом, и многие люди вынуждены лететь с пересадками и добираться до пункта назначения окольными путями.

В отличие от графа «Мир тесен», в случайной сети, в которой все вершины имеют приблизительно одинаковое количество соединений, удаление случайной вершины увеличивает длину кратчайшего пути в среднем незначительно, но одинаково для любой удаляемой вершины. В этом смысле случайные сети уязвимы для случайных возмущений, в то время как графы «Мир тесен» устойчивы. Однако графы «Мир тесен» уязвимы для направленных атак на хабы, в то время как в случайных сетях нельзя выбрать цели, уничтожение которых приведёт к катастрофическим последствиям.

Соответственно, вирусы эволюционировали таким образом, чтобы взаимодействовать с протеинами-хабами, такими как p53, тем самым внося существенные изменения в поведение клеток, благоприятствующие воспроизведению вирусов.

Конструирование графов «Мир тесен»

Основной механизм конструирования графов «Мир тесен» - Модель Уоттса — Строгаца

Построение графов «Мир тесен» с временным запаздыванием, позволяет создавать не только фракталы, но и хаос при правильных условиях или переход к хаосу в динамических сетях.

При решении задачи о степени диаметра конструируется граф, в котором количество соседей каждой вершины ограничено, в то время как расстояние между любой парой вершин (диаметр сети) минимизируется. Конструирование таких графов «Мир тесен» осуществляется в рамках усилий нахождения графов порядка, близкого к пределу Мура.

Другой путь конструирования графов «Мир тесен» с нуля показан у Бармпутиса и Мюррея, где строится сеть с очень маленьким средним расстоянием и очень большой средней кластеризацией. Быстрый алгоритм константной сложности дан вместе с измерениями надёжности полученных графов. В зависимости от области, можно начать с одного такого «ultra small-world» графа, и затем заново включить некоторые рёбра, или использовать некоторые маленькие такие сети как подграф большего графа.

Применение и приложения

Граф «Мир тесен» используют для моделирования в различных областях.

Приложения в социологии

Одно из преимуществ графов «Мир тесен» для общественного движения состоит в их защищённости от фильтрующих аппаратов, использующих сильно связанные вершины. Другое преимущество — лучшая эффективность в передаче информации при сохранении количества ссылок, необходимых для подключения к сети на минимальном уровне.

Модель графа «Мир тесен» напрямую применима к теории аффинити-групп, представленной в социологических аргументах Уильямом Финнеганом. Аффинити-группы — это общественные движения, являющиеся маленькими и полунезависимыми, но ставящие перед собой значительные цели и задачи. Несмотря на то, что отдельные участники относительно независимы и самостоятельны, несколько участников, обладающих высокой степенью связности, соответствуют хабам в графе «Мир тесен» — являются соединяющими вершинами, связывающими различные группы. Такая модель графа «Мир тесен» доказала чрезвычайно эффективную тактику организации протеста против действий полиции. Клей Ширки утверждает, что чем больше социальная сеть основывается на малых сетях, образуя граф «Мир тесен», тем более ценны вершины высокой степени связности в этой сети. То же самое может быть сказано и о модели аффинити-групп, где несколько людей в каждой группе соединены с внешними группами, которым позволена значительно большая степень мобилизации и адаптации. Практический пример этого — граф «Мир тесен» через аффинити-группы, который Уильям Финнеган наметил в общих чертах в протестах 1999 года в Сиэтле.

Приложение к наукам о Земле

Много сетей, изучаемых в геологии и геофизике, по характеристикам похожи на граф «Мир тесен». Сети, определённые в системе трещин и пористых субстанций, демонстрируют эти характеристики. Сейсмические сети региона Южной Калифорнии могут быть графами «Мир тесен». Приведенные выше примеры встречаются на самых разных пространственных масштабах, демонстрируя масштабную инвариантность феномена в науках о Земле.

Приложения к вычислениям

Графы «Мир тесен» были использованы для оценки возможности использования информации, хранящейся в больших базах данных. Мера оценки называется «Small World Data Transformation Measure». Чем больше связи базы данных похожи на граф «Мир тесен» — тем более вероятно, что пользователь будет в состоянии извлечь информацию в будущем. Это удобство обычно достигается за счёт количества информации, которое может храниться в том же хранилище.

P2P-сеть Freenet образует граф «Мир тесен», предоставляя возможность хранения и нахождения информации таким образом, чтобы эффективно масштабироваться при росте сети.

Графы «Мир тесен» в нейронных сетях головного мозга

Основная статья: Сети головного мозга топологии «Мир тесен»

Анатомические соединения в мозгу и сети синхронизации корковых нейронов представляют собой примеры графов «Мир тесен».

Граф «Мир тесен» из нейронов может проявлять свойства рабочей памяти. Компьютерная модель, разработанная Солла и др., имеет два стабильных состояния; это свойство называется бистабильностьюи считается важным в хранении памяти. Активирующий импульс генерируется самоподдерживающимися петлями коммуникационной активности среди нейронов. Второй импульс заканчивает эту активность. Пульсы переключают систему между стабильными состояниями: поток (запись «памяти») и состояние покоя (хранение памяти).

На более общем уровне многие крупные нейронные сети головного мозга, такие как зрительная система и ствол головного мозга, проявляют свойства графа «Мир тесен».

Граф «Мир тесен» в вычислительной лингвистике и в задачах по обработке текста

Об истории и развитии языков известно мало. У всех языков есть общие признаки: например, синтаксические и семантические категории. Для большинства языков характерен закон Ципфа. Для изучения различных свойств языков используются сети слов (то есть сети, в которых вершинам соответствуют слова, а рёбрам — какие-либо связи между словами). Также они могут быть использованы для обоснования различных гипотез о развитии языков. Например, исходя из сходства языков делается вывод о наличии у них общего предка. Однако сходство может быть вызвано влиянием языков друг на друга и заимствованием слов.

В семантической сети английского языка WordNet полисемия имеет огромное влияние на организацию семантического графа. Из-за неё семантический граф является графом «Мир тесен». Вершинами с высокой степенью (хабами), являются вершины, представляющие абстрактные понятия, такие как линия, голова, или круг.

Одна из задач обработки естественного языка — задача идентификации авторства текста. Один из методов — нахождение авторского инварианта. Сначала текст обрабатывается, из него удаляются шумовые слова (предлоги, союзы и т. п.). Затем строится сеть, в которой вершины соответствуют словам, а рёбра проводятся между вершинами, которые соответствуют словам, которые в тексте расположены рядом. Установлено, что полученный граф является графом «Мир тесен». Если посчитать у сети, построенной по литературному произведению, некоторые параметры (например, среднюю степень вершины, коэффициент кластеризации, корреляцию степени вершин), то можно заметить, что в произведениях одного автора эти параметры изменяются в относительно небольшом диапазоне, в то время как у разных авторов эти параметры отличаются гораздо сильнее.

Если представить статьи Википедии как вершины, а ссылки между страницами представить рёбрами между соответствующими вершинами, то получается граф, обладающий свойствами графа «Мир тесен». Причинами этого являются уже указанная выше принадлежность к классу графов «Мир тесен» семантической сети слов, а также наличие в Википедии списков и категорий, выполняющих роль хабов. Высокая степень связности Википедии дополнительно поддерживается проектом «Связность».

Граф «Мир тесен» с распределением длины ссылок

Модель графа «Мир тесен» включает равномерное распределение длин ссылок, подчиняющееся степенному закону распределения, среднее расстояние между двумя вершинами изменяется в зависимости от силы распределения.

Децентрализованный алгоритм поиска

Если в эксперименте Стэнли Милгрэма исследователю требуется найти именно кратчайший путь, то ему надо отправить письма всем своим знакомым и заставить их сделать то же самое. Такой «флуд» в сети достигнет цели так быстро, как только возможно, но такая массовая рассылка практически невозможна. Другой вариант эксперимента — отправлять письмо только одному человеку за раз. В результате проведения эксперимента Мир тесен было совершено поразительное алгоритмическое открытие: в графе «Мир тесен» людям, не знающим всю структуру графа, а имеющим только локальную информацию (о своих знакомых), удаётся коллективно найти относительно короткий путь к цели (наличие относительно короткого пути является известным свойством графов типа «Мир тесен»).

Возникает вопрос: почему социальная сеть структурирована таким образом, что такой децентрализованный алгоритм поиска даёт оптимальные результаты? Подобные децентрализованные алгоритмы поиска работают также во Всемирной паутине, в нейронных сетях и во множестве других областей. Следовательно, понимание алгоритмов работы децентрализованных поисковых алгоритмов обеспечит их широкое применение.

Для дальнейших рассуждений необходимо сформулировать более строгое определение децентрализованного алгоритма поиска. Алгоритм рекурсивный: мы стоим в вершине $v$, нам нужно достичь вершины $t$, мы знаем лишь соседей вершины $v$, среди них нужно выбрать вершину $w$ и запустить алгоритм от неё. Децентрализованный алгоритм оценивается временем доставки — ожидаемым количеством шагов, необходимых для достижения цели, при этом граф «Мир тесен», стартовая и целевая вершины генерируются случайным образом. Цель исследований — найти полилогарифмические относительно $n$ алгоритмы децентрализованного поиска. Эти исследования проводил Джон Клейнберг в работе «Complex networks and decentralized search algorithms».

См. также

• Модель Эрдёша — Реньи
• Модель Барабаши — Альберт
• Число Эрдёша
• Безмасштабная сеть
• Шесть шагов до Кевина Бэйкона
• Мир тесен
• Социальная сеть (социология)
• Число Данбара

Литература

• Jin Chen. Systematic Assessment of Protein Interaction Data using Graph Topology Approaches (англ.). — 2006. (недоступная ссылка)
• Maaike Snelder. Designing Robust Road Networks A general design method applied to the Netherlands. — 2010. — ISBN 978-90-5584-135-6. Архивная копия от 27 мая 2014 на Wayback Machine
• Stefano Boccaletti, Vito Latora, Yamir Moreno. Handbook on Biological Networks. — 2010. — ISBN 978-981-283-979-7.
• F. Lamanna and G. Longo. Connectivity and stability of the air network in the Southeastern Europe: A Small World approach (англ.) // JOURNAL OF TRANSPORT AND SHIPPING. — 2007. — № 4. — ISSN 1109–9437. Архивировано 4 марта 2016 года.
• Robert Hillard. Information-Driven Business (неопр.). — Wiley, 2010. — ISBN 978-0-470-62577-4.
• Клей Ширки. Here Comes Everybody (неопр.). — Penguin Group, 2008. — 327 с. — ISBN 978-1-59420-153-0.
• M. D. Humphries, K. Gurney and T. J. Prescott, Phil. Trans. Is there a brainstem substrate for action selection? (англ.) // R. Soc. B : journal. — 2007. — doi:10.1098/rstb.2007.2057.
• K.E. Joyce, S. Hayasaka, J.H. Burdette, P.J. Laurienti. The ubiquity of small-world networks Q.K. Telesford, (англ.) // Brain Connect : journal. — 2011. — P. 367—375. — doi:10.1089/brain.2011.0038.
• Finnegan, William. Affinity Groups and the Movement Against Corporate Globalization (англ.) // Goodwin, Jeff and Jasper, James M The Social Movements Reader: Cases and Concepts (Wiley Blackwell Readers in Sociology) : journal. — Wiley-Blackwell, 2003. — Vol. 1. — P. 210—218. — ISBN 978-0631221968.
• X. S. Yang. Small-world networks in geophysics (неопр.) // Geophys. Res. Lett., 28(13). — 2001. — С. 2549—2552.
• A. Jimenez, K. F. Tiampo, A. M. Posadas. Small-world in a seismic network: the California case (англ.) // Nonlin. Processes Geophys., 15 : journal. — 2008. — P. 389—395.
• Jon Kleinberg. Complex networks and decentralized search algorithms : Proceedings of the International Congress of Mathematicians, Madrid, Spain. — 2006. (недоступная ссылка)
• Xiangdong Che, M. Ali, R.G. Reynolds. Robust evolution optimization at the edge of chaos: Commercialization of culture algorithms : Evolutionary Computation (CEC), 2010 IEEE Congress on. — 2010. — ISBN 978-1-4244-6909-3.
• Sporns, Olaf; Tononi G., Edelman G. M. Organization, development and function of complex brain networks (англ.) // Trends Cogn Sci. : journal. — 2004. — Vol. 8, no. 9. — P. 418—425.. — doi:10.1016/j.tics.2004.07.008. — PMID 15350243.
• Yu, Shan; D. Huang, W. Singer and D. Nikolić. A Small World of Neuronal Synchrony (неопр.) // Cerebral Cortex. — 2008. — Т. 18, № 12. — С. 2891—2901. — doi:10.1093/cercor/bhn047. — PMID 18400792. — PMC 2583154.
• M.Barthelemy, L.Amaral. Small-world networks: Evidence for a crossover picture (англ.) // Phys. Rev. Lett. : journal. — 1999. — Vol. 82, no. 15. — P. 3180. — doi:10.1103/PhysRevLett.82.3180. — . — arXiv:cond-mat/9903108.
• R.Cohen, S.Havlin, and D.ben-Avraham. Structural properties of scale free networks (неопр.) // Handbook of graphs and networks. — Wiley-VCH, 2002, 2002. — № Chap. 4.
• R. Cohen, S.Havlin. Scale-free networks are ultrasmall (англ.) // Phys. Rev. Lett. : journal. — 2003. — Vol. 90, no. 5. — P. 058701. — doi:10.1103/PhysRevLett.90.058701. — . — arXiv:cond-mat/0205476. — PMID 12633404.

• P.Bork, LJ Jensen, C. von Mering, A.Ramani, I.Lee, EM.Marcotte. Protein interaction networks from yeast to human (англ.) // Current Opinion in Structural Biology. — Elsevier, 2004. — Vol. 14, no. 3. — P. 292—299. — doi:10.1016/j.sbi.2004.05.003. — PMID 15193308.
• V.Van Noort, B.Snel, MA.Huynen. The yeast coexpression network has a small-world, scale-free architecture and can be explained by a simple model (англ.) // EMBO Rep. : journal. — 2004. — March (vol. 5, no. 3). — P. 280—284. — doi:10.1038/sj.embor.7400090. — PMID 14968131. — PMC 1299002.
• X. S. Yang. Fractals in small-world networks with time-delay (неопр.) // Chaos, Solitons & Fractals. — 2002. — Т. 13. — С. 215—219.
• X. S. Yang. Chaos in small-world networks (неопр.) // Phys. Rev. E 63, 046206. — 2001.
• W. Yuan, X. S. Luo, P. Jiang, B. Wang, J. Fang. Transition to chaos in small-world dynamical network (англ.) : journal. Архивировано 3 января 2014 года.
• D.Barmpoutis and R.M. Murray. Networks with the Smallest Average Distance and the Largest Average Clustering (англ.) : journal. — 2010.
• D. Li, K. Kosmidis, A. Bunde, S. Havlin. Dimension of spatially embedded networks (англ.) // Nature Physics : journal. — 2011. — doi:10.1038/nphys1932. — .

Ссылки

• Патент US8495206 - Method and system for job scheduling in distributed data processing system ... - Google Патенты (англ.).
• Duncan J. Watts & Steven H. Strogatz. Collective dynamics of ‘small-world’ networks (англ.). Nature Publishing Group, a division of Macmillan Publishers Limited. (1999).
• A.Barrat and M.Weigt. On the properties of small-world network models (англ.). Europ. Phys. J. B 13, 547 (2000) (1999).
• S.N. Dorogovtsev, J.F.F. Mendes. Evolution of networks (англ.). Adv. Phys. 51, 1079 (2002) (2002).
• Dionysios Barmpoutis, Richard M. Murray. Noise Propagation in Biological and Chemical Reaction Networks (англ.). California Institute of Technology.
• S. Boccaletti, V. Latora, Y. Moreno, M. Chavez., D.-U. Hwang. Complex networks: Structure and dynamics (англ.). Elsevier.
• Mariano Sigman, Guillermo A. Cecchi. Global organization of the Wordnet lexicon  (неопр.) (2001).
• Information Theory & Business Intelligence Strategy — Small Worlds Data Transformation Measure — MIKE2.0, the open source methodology for Information Development  (неопр.).
• Sandberg, Oskar Searching in a Small World  (неопр.).
• Cohen, Philip. Small world networks key to memory  (неопр.) (26 мая 2004).
• Sara Solla. Lecture & Slides: Self-Sustained Activity in a Small-World Network of Excitable Neurons  (неопр.).
• Lucas Antiqueira, Thiago Alexandre Salgueiro Pardo, Maria das Gra ̧cas Volpe Nunes, Osvaldo Novais de Oliveira Jr., Luciano da Fontoura Costa. Some issues on complex networks for author characterization  (неопр.) (2006). doi:10.1.1.94.3070.
• Adolfo Paolo Masucci, Alkiviadis Kalampokis, Victor Martínez Eguíluz, Emilio Hernández-García. Wikipedia Information Flow Analysis Reveals the Scale-Free Architecture of the Semantic Space (англ.) (28 февраля 2011). doi:10.1371/journal.pone.001733.
• Ricard V. Sole, Bernat Corominas Murtra, Sergi Valverde, Luc Steels. Language Networks: their structure, function and evolution  (неопр.) (9 января 2007).
• Dynamic Proximity Networks by Seth J. Chandler, The Wolfram Demonstrations Project.
• Small-World Networks entry on Scholarpedia (by Mason A. Porter)