Курносый куб

Курно́сый куб, или плосконо́сый куб, — полуправильный многогранник (архимедово тело) с 38 гранями, составленный из 6 квадратов и 32 правильных треугольников. В каждой из его 24 одинаковых вершин сходятся одна квадратная грань и четыре треугольных. Треугольные грани делятся на две группы: 8 из них окружены только другими треугольными, остальные 24 — квадратной и двумя треугольными.

Курносый куб
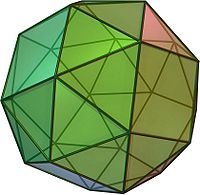«Правый» вариант (вращающаяся модель, 3D-модель)
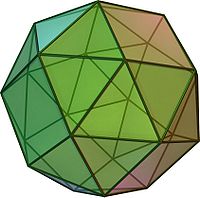«Левый» вариант (вращающаяся модель, 3D-модель)
Тип	архимедово тело
Свойства	выпуклый, изогональный, хиральный
Комбинаторика
Элементы	38 граней 60 рёбер 24 вершины Χ = 2
Грани	32 треугольника, 6 квадратов
Конфигурация вершины	34.4
Двойственный многогранник	пентагональный икоситетраэдр
Вершинная фигура
Развёртка Развёртка для «левого» варианта
Классификация
Обозначения	sC
Символ Шлефли	sr{4,3}
Группа симметрии	O (хиральная октаэдрическая)
Медиафайлы на Викискладе

Имеет 60 рёбер равной длины.

Название «курносый куб» (лат. cubus simus) дал этому многограннику Иоганн Кеплер в трактате 1619 года «Гармония мира». Гарольд Коксетер, отметив, что многогранник родствен октаэдру в той же мере, что и кубу, предлагал называть его «курносым кубооктаэдром».

В отличие от большинства других архимедовых тел, курносый куб (наряду с курносым додекаэдром) является хиральным и существует в двух разных зеркально-симметричных (энантиоморфных) вариантах — «правом» и «левом».

Преобразование ромбокубооктаэдра в «левый» и «правый» курносые кубы.

Метрические характеристики и углы

При определении метрических свойств курносого куба приходится решать кубические уравнения и пользоваться кубическими корнями — тогда как для ахиральных архимедовых тел и для платоновых тел не требуется ничего сложнее квадратных уравнений и квадратных корней. Поэтому курносый куб, в отличие от платоновых и ахиральных архимедовых тел, не допускает евклидова построения. То же верно и для курносого додекаэдра, а также для двойственных им каталановых тел.

При описании метрических свойств и углов курносого куба важную роль играет константа трибоначчи:

$t={\frac {1}{3}}\left(1+{\sqrt[{3}]{19-3{\sqrt {33}}}}+{\sqrt[{3}]{19+3{\sqrt {33}}}}\right)\approx 1{,}8392868.$.

Если курносый куб имеет ребро длины $a$, его площадь поверхности и объём выражаются как

$S=\left(6+8{\sqrt {3}}\right)a^{2}\approx 19{,}8564065a^{2},$

$V={\sqrt {\frac {613t+203}{9(35t-62)}}}\;a^{3}\approx 7{,}8894774a^{3}.$

Радиус описанной сферы (проходящей через все вершины многогранника) при этом будет равен

$R={\sqrt {\frac {3-t}{4(2-t)}}}\;a\approx 1{,}3437134a;$

радиус полувписанной сферы (касающейся всех рёбер в их серединах) —

$\rho ={\sqrt {R^{2}-{\frac {a^{2}}{4}}}}={\sqrt {\frac {1}{4(2-t)}}}\;a\approx 1{,}2472232a.$

Вписать в курносый куб сферу — так, чтобы она касалась всех граней, — невозможно. Радиус наибольшей сферы, которую можно поместить внутри курносого куба с ребром $a$ (она будет касаться только всех квадратных граней в их центрах), равен

$r_{4}={\sqrt {R^{2}-{\frac {a^{2}}{2}}}}={\sqrt {\frac {t-1}{4(2-t)}}}\;a\approx 1{,}1426135a.$

Расстояние от центра многогранника до любой треугольной грани превосходит $r_{4}$ и равно

$r_{3}={\sqrt {R^{2}-{\frac {a^{2}}{3}}}}={\sqrt {\frac {t+1}{12(2-t)}}}\;a\approx 1{,}2133558a.$

Двугранные углы между двумя смежными треугольными гранями курносого куба равны $\alpha _{33}=\arccos \,{\frac {1-2t}{3}}\approx 153{,}23^{\circ },$ между смежными квадратной и треугольной гранями $\alpha _{43}=\arccos \left(-{\sqrt {1-{\frac {2}{3t}}}}\right)\approx 142{,}98^{\circ }.$

Телесный угол при вершине равен $3\alpha _{33}+2\alpha _{43}-3\pi \approx 1{,}14\pi .$

В координатах

«Левый» курносый куб можно разместить в декартовой системе координат так, чтобы координаты 12 его вершин были всевозможными чётными перестановками тех троек чисел $(\pm t;\pm 1;\pm t^{-1}),$ среди которых чётное число отрицательных, а координаты остальных 12 вершин — всевозможными нечётными перестановками тех троек, среди которых нечётное число отрицательных.

Если поступить наоборот — взять чётные перестановки троек с нечётным числом минусов и нечётные перестановки троек с чётным числом минусов — получим «правый» вариант курносого куба.

Начало координат $(0;0;0)$ в обоих случаях будет центром описанной и полувписанной сфер многогранника.

Ссылки

• Weisstein, Eric W. Курносый куб (англ.) на сайте Wolfram MathWorld.

Литература

• М. Веннинджер. Модели многогранников. — Мир, 1974.
• Многоугольники и многогранники // Энциклопедия элементарной математики. Книга четвёртая. Геометрия / Под ред. П. С. Александрова, А. И. Маркушевича, А. Я. Хинчина. — М.: Государственное издательство физико-математической литературы, 1963. — С. 382—447.
• Л. А. Люстерник. Выпуклые фигуры и многогранники. — М.: Государственное издательство технико-теоретической литературы, 1956.