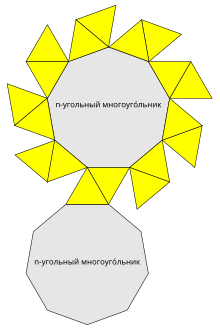
Антипризма
Антипризма — полуправильный многогранник, у которого две параллельные грани (основания) — равные между собой правильные n-угольники, а остальные 2n граней (боковые грани) — правильные треугольники.
| Антипризма на -угольнике | |||
|---|---|---|---|
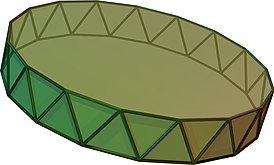 Антипризма на 17-угольнике | |||
| Тип | полуправильный многогранник | ||
| Комбинаторика | |||
| Элементы |
|
||
| Грани | треугольников, 2 -угольника | ||
| Конфигурация вершины | 3.3.3. | ||
| Двойственный многогранник | трапецоэдр | ||
| Классификация | |||
| Обозначения | |||
| Символ Шлефли |
|
||
| Диаграмма Дынкина |
|
||
| Группа симметрии | |||
| Группа вращения | |||
| Количественные данные | |||
| Длина ребра | |||
| Площадь поверхности | |||
| Объём | |||
Октаэдр является антипризмой с треугольными основаниями. Икосаэдр сложен из пятиугольной антипризмы и двух правильных пятиугольных пирамид.
Объем и площадь поверхности
правитьПусть — длина ребра правильной антипризмы. Тогда её объем вычисляется по формуле:
а площадь поверхности по формуле:
Вариации и обобщения
править- Скрученная квадратная антипризма получается из антипризмы поворотом одного из оснований при сохранении комбинаторной структуры граней рёбер и вершин.
- Многогранник Шёнхардта — скрученная треугольная антипризма.
| Многогранник | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Мозаика | ||||||||||||
| Конфигурация | V2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | ...∞.3.3.3 |
| *n62 варианты симметрии правильных мозаик: {6,n} | ||||||||
|---|---|---|---|---|---|---|---|---|
| Сферические | Евклидовы | Гиперболические мозаики | ||||||
| {6,2} |
{6,3} |
{6,4} |
{6,5} |
{6,6} |
{6,7} |
{6,8} |
... | {6,∞} |
См. также
правитьЭто заготовка статьи по математике. Помогите Википедии, дополнив её. |
В статье не хватает ссылок на источники (см. рекомендации по поиску). |