Антиподера

Обзорная статья: Подера

Антиподе́ра (фр. antipodaire, от др.-греч. άντί- — против и подера; англ. antipedal) кривой относительно точки — кривая, для которой данная кривая есть подера относительно той же точки.

Парабола — антиподера прямой

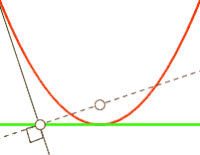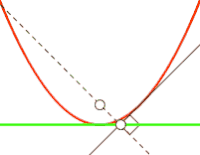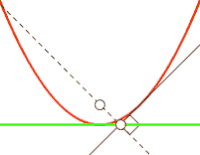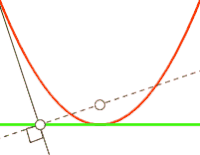
Например, парабола есть антиподера прямой, если полюс антиподеры совпадает с фокусом параболы, как показано на рисунке справа.

Антиподера кривой есть инверсия этой кривой с последующим полярным преобразование кривой, полюсы которых совпадают с полюсом антиподеры. Также антиподера кривой есть инверсия подеры инверсии этой кривой, полюсы которых совпадают с полюсом антиподеры.

Полное определение антиподеры

Окружность — антиподера улитки Паскаля

Антиподе́ра, или отрицательная подера, или первая отрицательная подера ( англ. antipedal; negative pedal; first negative pedal), кривой относительно точки — кривая, подера которой относительно той же точки есть исходная кривая. Другими словами, антиподера — огибающая кривая перпендикуляров, проведённых через точки исходной кривой к прямым, соединяющим точки исходной кривой с фиксированной точкой, которая называется полюсом, или центром, или точкой подеры.

Построение антиподеры исходя из уже построенной её подеры называется построением с помощью подеры.

Например, всегда получится коническое сечение, если осуществить построение с помощью подеры из окружности или прямой.

Антриподе́ры степене́й вы́ше пе́рвой определяются как антиподеры антиподер предыдущей степени с одним и тем же полюсом.

• Антиподеры секстики Кэли и подеры кубики Чирнгауза шести степеней
• 
  Кардиоида — 1-я антиподера секстики Кэли — 6-я подера кубики Чирнгауза
• 
  Окружность — 2-я антиподера секстики Кэли, кардиоида — 5-я подера кубики Чирнгауза
• 
  Точка — 3-я антиподера секстики Кэли, окружность — 4-я подера кубики Чирнгауза
• 
  Прямая — 4-я антиподера секстики Кэли, точка — 3-я подера кубики Чирнгауза
• 
  Парабола — 5-я антиподера секстики Кэли, прямая — 2-я подера кубики Чирнгауза
• 
  Кубика Чирнгауза — 6-я антиподера секстики Кэли, парабола — 1-я подера кубики Чирнгауза

Определение антиподеры через инверсию

Имеет место схема преобразований кривых для подеры, инверсии и полярного преобразования кривой, показанная на рисунке справа, из которой вытекает следующее два утверждения:

• антиподера кривой есть инверсия с последующим полярным преобразованием кривой, окружности преобразования которых совпадают, а полюсы совпадают с полюсом подеры;
• антиподера кривой есть инверсия подеры инверсии кривой, окружности преобразования которых совпадают, а полюсы совпадают с полюсом антиподеры.

Уравнения антиподеры

Параметрические уравнения антиподеры

Параметрические уравнения антиподеры на вещественной плоскости

В общем случае, для параметрически заданной кривой $\mathbf {z} (t)=(x(t),\;y(t))$, имеющей производную $\mathbf {z} '(t)=(x'(t),\;y'(t))$, антиподера

$\operatorname {antipedal} [\mathbf {z} ,\;\mathbf {z} _{0}](t)=\mathbf {Z} (t)=(X(t),\;Y(t))$

относительно точки $\mathbf {z} _{0}=(x_{0},\;y_{0})$ задаётся следующими уравнениями:

$X={\frac {((x-x_{0})x-(y-y_{0})^{2})y'-(2x-x_{0})(y-y_{0})x'}{(x-x_{0})y'-(y-y_{0})x'}}=$

$=2x-x_{0}-y'{\frac {(x-x_{0})^{2}+(y-y_{0})^{2}}{(x-x_{0})y'-(y-y_{0})x'}}=$

$=x-(y-y_{0}){\frac {(x-x_{0})x'+(y-y_{0})y'}{(x-x_{0})y'-(y-y_{0})x'}},$

$Y={\frac {-((y-y_{0})y-(x-x_{0})^{2})x'+(2y-y_{0})(x-x_{0})y'}{(x-x_{0})y'-(y-y_{0})x'}}=$

$=2y-y_{0}+x'{\frac {(x-x_{0})^{2}+(y-y_{0})^{2}}{(x-x_{0})y'-(y-y_{0})x'}}=$

$=y+(x-x_{0}){\frac {(x-x_{0})x'+(y-y_{0})y'}{(x-x_{0})y'-(y-y_{0})x'}}.$

Эти основные уравнения можно принять за определение антиподеры.

Доказательство

Уравнение прямой $(X(t),\;Y(t))$, проходящей через две точки:

• полюс антиподеры $(x_{0},\;y_{0})$,
• текущую точку исходной кривой $(x,\;y)$,

есть

${\frac {Y-y}{y_{0}-y}}={\frac {X-x}{x_{0}-x}},$

или

$Y-y={\frac {y_{0}-y}{x_{0}-x}}(X-x).$

Тогда уравнение перпендикулярной прямой, проходящей через текущую точку исходной кривой $(x,\;y)$

$Y-y=-{\frac {x_{0}-x}{y_{0}-y}}(X-x).$

Антиподера исходной кривой — огибающая семейства кривых

$U(X,\;Y,\;t)=Y-y+{\frac {x_{0}-x}{y_{0}-y}}(X-x)=0$ —

определяется системой уравнений

$U(X,\;Y,\;t)={\frac {\partial U(X,\;Y,\;t)}{\partial t}}=0.$

Находим:

${\frac {\partial U(X,\;Y,\;t)}{\partial t}}={\frac {\partial }{\partial t}}(Y-y+{\frac {x_{0}-x}{y_{0}-y}}(X-x))=$

$=-y'-X{\frac {x'}{y_{0}-y}}+X{\frac {(x_{0}-x)y'}{(y_{0}-y)^{2}}}-$

${}-{\frac {(x_{0}-x)x'}{y_{0}-y}}+{\frac {xx'}{y_{0}-y}}-{\frac {(x_{0}-x)xy'}{(y_{0}-y)^{2}}}=0,$

$X((x_{0}-x)y'-(y_{0}-y)x')=$

$=(y_{0}-y)(x_{0}-x)x'-(y_{0}-y)xx'+$

${}+(x_{0}-x)xy'+(y_{0}-y)^{2}y',$

$X={\frac {((x-x_{0})x-(y-y_{0})^{2})y'-(2x-x_{0})(y-y_{0})x'}{(x-x_{0})y'-(y-y_{0})x'}}.$

$Y=y-{\frac {x_{0}-x}{y_{0}-y}}(X-x)=$

$=y+{\frac {x-x_{0}}{y-y_{0}}}(y-y_{0}){\frac {(x-x_{0})x'+(y-y_{0})y'}{(x-x_{0})y'-(y-y_{0})x'}}=$

$=y+(x-x_{0}){\frac {(x-x_{0})x'+(y-y_{0})y'}{(x-x_{0})y'-(y-y_{0})x'}}.$

В частном случае, относительно полюса $\mathbf {z} _{0}=(0,\;0)$ в начале координат, основные уравнения будут такими:

$X={\frac {(x^{2}-y^{2})y'-2xyx'}{xy'-yx'}}=$

$=2x-y'{\frac {x^{2}+y^{2}}{xy'-yx'}}=$

$=x-y{\frac {xx'+yy'}{xy'-yx'}},$

$Y={\frac {-(y^{2}-x^{2})x'+2xyy'}{xy'-yx'}}=$

$=2y+x'{\frac {x^{2}+y^{2}}{xy'-yx'}}=$

$=y+x{\frac {xx'+yy'}{xy'-yx'}}.$

Примеры антиподеры

• Парабола — антиподера прямой.

Источники

• Антиподера // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 75.
• Гильберт Д., Кон-Фоссен С. Наглядная геометрия: Пер. с нем. С. А. Каменецкого. 3-е изд. М.: Наука, 1981. 144 с., ил.
• Иванов А. Б. Подера // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 4 Ок—Сло. М.: «Советская Энциклопедия», 1984. 1216 стб., ил. Стб. 370.
• Коренцова М. М. Колин Маклорен. 1698—1746. М.: Наука, 1998. 144 с., ил. (Научно-биографическая литература.) ISBN 5-02-003691-9.
• Подера и антиподера // Большая советская энциклопедия. (В 30 томах) Гл. ред. А. М. Прохоров. Изд. 3-е. М.: «Советская энциклопедия», 1975. Т. 20. Плата — проб. 1975. 608 с. с илл., 17 л. илл., 4 л. карт. С. 109.
• Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка. М.: Физматлит, 1961. 271 с., ил.
• Яглом И. М., Атанасян Л. С. Геометрические преобразования // Энциклопедия элементарной математики, книга четвёртая — геометрия / Гл. ред. П. С. Александров, А. И. Маркушевич, А. Я. Хинчин. Ред. книги 4: В. Г. Болтянский, И. М. Яглом. М.: Физматгиз, 1963. 568 с., ил. С. 49—158.
• Alfred Gray. Modern differential geometry of curves and surfaces with Mathematica. Third Edition by Elsa Abbena and Simon Salamon. Studies in Advanced Mathematics: Chapman and Hall/CRC, 2006. 982 p.
• Ferréol Robert. Pedal of a Curve // ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES Архивная копия от 10 апреля 2023 на Wayback Machine
• Lawrence J. D. A Catalog of Special Plane Curves. New York: Dover Publications, Inc., 1972. 218 p.
• Weisstein Eric W. Negative Pedal Curve // Wolfram MathWorld Архивная копия от 30 ноября 2022 на Wayback Machine
• Zwikker C. The Advanced Geometry of Plane Curves and Their ApplicationsThe Advanced Geometry of Plane Curves and Their Applications. New York: Dover Publications, Inc., 1963. 299 p. ISBN 0486610780. ISBN 9780486610788.