Делящаяся плитка

Делящаяся плитка (англ. rep-tile) — понятие геометрии мозаик, фигура, которую можно разрезать на меньшие копии самой фигуры. В 2012 обобщение делящихся мозаик с названием self-tiling tile set (набор плиток с самозамощением) было предложено английским математиком Ли Сэлоусом в журнале Mathematics Magazine .

«Сфинкс» полиамондная самовоспроизводящаяся мозаика. Четыре копии сфинкса можно сложить вместе и получить большего сфинкса.

Набор делящихся плиток, включая плитку «Сфинкс», две рыбы и 5-треугольник

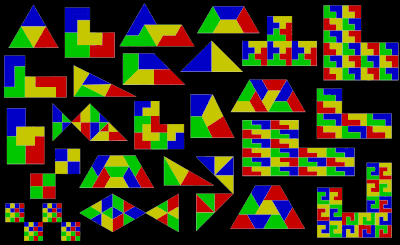
Терминология

Делящиеся плитки обозначаются rep-n, если разрезание использует n копий. Такие фигуры обязательно формируют протоплитку замощения плоскости, во многих случаях образующую непериодичную мозаику. Разрезание делящейся плитки с использованием различных размеров называется нерегулярной делящейся плиткой. Если такое разрезание использует n копий, фигуру обозначают irrep-n. Если все подплитки имеют различные размеры, разрезание называют совершенным. Фигуры rep-n или irrep-n являются, очевидно, irrep-(kn − k + n) для любого k > 1 (просто заменяем самый маленький элемент разрезания на n ещё более мелких элементов). Порядком плитки, будь то rep- или irrep-плитка, называется наименьшее возможное число частей, на которые плитку можно разрезать (сохраняя форму частей).

Примеры

Определение апериодичной мозаики (мозаики «Вертушка») путём повторяющегося разрезания и растяжения делящейся плитки.

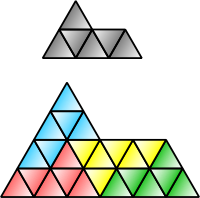
Любой квадрат, прямоугольник, параллелограмм, ромб или треугольник является rep-4. Гексиамонд «Сфинкс» (верхний рисунок) является rep-4 и rep-9 и является одним из нескольких известных самовоспроизводящихся пятиугольников. Кривая Госпера является rep-7. Снежинка Коха является irrep-7 — шесть меньших снежинок одинакового размера, вместе со снежинкой втрое большей площади, можно скомбинировать для получения одной снежинки большего размера.

Прямоугольный треугольник с длинами сторон в пропорции 1:2 является rep-5, а его rep-5 разрезание образует базис апериодичной мозаики «Вертушка». По теореме Пифагора гипотенуза треугольника rep-5 имеет длину √5.

Международный стандарт ISO 216 определяет размеры листов бумаги с помощью √2 — длинная сторона прямоугольного листа бумаги в квадратный корень из 2 раз длинней короткой стороны. Прямоугольники с такой формой являются rep-2. Прямоугольник (или параллелограмм) является rep-n, если его характеристическое отношение равно √n:1(но не только, например √3: √2 является rep-6, как и прямоугольник √6:1). Равнобедренный прямоугольный треугольник является rep-2.

Делящаяся плитка и симметрия

Некоторые делящиеся плитки, такие как квадрат и правильный треугольник, симметричны и остаются идентичными при зеркальном отражении. Другие, такие как сфинкс, являются асимметричными и существуют в двух различных формах, связанных зеркальным отражением. Разрезание сфинкса и некоторых других асимметричных делящихся плиток требует использования обоих видов — исходной фигуры и её зеркального образа.

Делящаяся плитка и полиформы

Некоторые делящиеся плитки основываются на полиформах, таких как полиамонды и полимино, или на фигурах, созданных соединением правильных треугольников и квадратов ребро-к-ребру.

Квадраты

Если полимино квадрируемо или может замостить прямоугольник, то оно будет делящейся плиткой, поскольку прямоугольником можно замостить квадрат (который сам по себе является частным случаем прямоугольника). Это легко можно видеть в элементах октамино, состоящих из восьми квадратов. Две копии некоторых элементов октамино заполняют квадрат, поэтому эти элементы также являются делящимися плитками rep-16.

Делящаяся плитка, основанная на квадрируемых октамино

Четыре копии одних и тех же нонамино и нонакингов замощают квадрат, поэтому эти полиформы являются также делящимися плитками rep-36.

Делящиеся плитки, созданные из квадрируемых нонамино и 9-поликингов (нонакингов)

Правильные треугольники

Таким же образом, если полиамонд замощает правильный треугольник, он будет также делящейся плиткой.

Делящаяся плитка, созданная из правильных треугольников

Ракетоподобная делящаяся плитка (додекамонд), созданная из двенадцати правильных треугольников

Прямоугольные треугольники

Полиформы, основанные на равнобедренных прямоугольных треугольниках (с углами 45°-90°-45°), известны как полиаболо. Бесконечное число из них являются делящимися плитками. Более того, простейшей из всех делящихся плиток является (одиночный) равнобедренный прямоугольный треугольник. Он является rep-2, если разделить высотой гипотенузу. Rep-2 делящиеся плитки являются rep-2ⁿ плитками и rep-4,8,16+ треугольники порождают дальнейшие делящиеся плитки. Нижеприведённые плитки найдены путём отбрасывания половины плиток и перестановки оставшихся, пока они не станут дополнением при зеркальной симметрии внутри прямоугольного треугольника. Одна плитка напоминает рыбу, образованную тремя правильными треугольниками.

Делящиеся плитки, основанные на прямоугольных треугольниках

Напоминающая рыбу делящаяся плитка, образованная тремя правильными треугольниками

Напоминающая рыбу делящаяся плитка, образованная четырьмя правильными треугольниками

Пятиугольные делящиеся плитки

Треугольные и квадратные (четырёхсторонние) делящиеся плитки встречаются часто, а пятиугольные делящиеся плитки редки. Долгое время считалось, что сфинкс является единственным примером, но немецкий/новозеландский математик Карл Шерер и американский математик Джордж Зихерман нашли дополнительные примеры, включая двойную пирамиду и удлинённую версию сфинкса. Эти пятиугольные делящиеся плитки проиллюстрированы на страницах Math Magic, которые поддерживает американский математик Эрих Фридман. Однако сфинкс остаётся единственной известной пятиугольной делящейся плиткой, подкопии которой имеют тот же размер.

Пятиугольная делящаяся плитка, обнаруженная Карлом Шерером

---

Делящиеся плитки и фракталы

Делящиеся плитки как фракталы

Делящиеся плитки можно использовать для создания фракталов или фигур, которые самоподобны во всё меньшем и меньшем размере. Фрактал (из делящейся плитки) образуется делением делящейся плитки (возможным) удалением нескольких копий разделённой фигуры, продолжая процесс рекурсивно. Например, ковёр Серпинского образуется этим способом из делящейся плитки (квадрата) делением на 27 меньших квадратов, а треугольник Серпинского образуется из делящейся плитки (правильного треугольника) делением на четыре меньших треугольника. Если удалять одну из копий, rep-4 L-тримино можно использовать для создания четырёх фракталов, два из которых идентичны, если не принимать во внимание ориентацию.

Геометрическое разрезание L-тримино (rep-4)	Фрактал, основанный на L-тримино (rep-4)
Другой фрактал, основанный на L-тримино	Третий фрактал, основанный на L-тримино

Фракталы в качестве делящихся плиток

Поскольку фракталы являются самоподобными, многие из них являются также самозамощаемыми, а потому являются делящимися плитками. Например, Треугольник Серпинского является rep-3, замощённым тремя копиями себя, а ковёр Серпинского является rep-8, замощённым восемью копиями себя.

Треугольник Серпинского как три меньшие копии треугольника Серпинского

Ковёр Серпинского как восемь меньших копий ковра Серпинского

Делящиеся плитки с множественными разрезаниями

Многие из известных делящихся плиток являются rep-n² для всех положительных значений числа n. В частности, это верно для трёх трапеций, включая образованную из трёх правильных треугольников, для трёх пентамино (L-тримино, L-тетрамино P-пентамино) и гексимонда «Сфинкс».

Бесконечные мозаики

Среди правильных многоугольников только треугольник и прямоугольник можно разрезать на меньшие равные копии себя. Однако правильный шестиугольник может быть разрезан на шесть равносторонних треугольников, каждый из которых может быть разрезан на правильный шестиугольник и три правильных треугольника. Это является базисом бесконечного замощения шестиугольника шестиугольниками. Таким образом, шестиугольник является irrep-∞ или irrep-бесконечной делящейся плиткой.

Замощение правильного шестиугольника бесконечной копией себя

См. также

• Мозаика
• Самовоспроизведение
• Рептилии (литография)

Литература

• М. Гарднер. Математические досуги. — Москва: «Мир», 1972.
• M. Gardner. Rep-Tiles // The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems. — New York: W. W. Norton, 2001. — С. 46–58..
• M. Gardner. The Unexpected Hanging and Other Mathematical Diversions. — Chicago: Chicago University Press, 1991. — С. 222–233.
• C. D. Langford. Uses of a Geometric Puzzle // Math. Gaz. — 1940. — Вып. 260.
• Viorel Niţică. MASS selecta. — Providence, RI: American Mathematical Society, 2003. — С. 205–217..
• Lee Sallows. On self-tiling tile sets // Mathematics Magazine. — 2012. — Т. 85, вып. 5. — С. 323–333. — doi:10.4169/math.mag.85.5.323..
• Scherer, Karl. «A Puzzling Journey to the Reptiles and Related Animals», 1987
• Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 213—214, 1991.

Ссылки

Rep-плитки

• Mathematics Centre Sphinx Album: https://web.archive.org/web/20130409094814/http://blackdouglas.com.au/taskcentre/sphinx.htm
• Clarke, A. L. «Reptiles.» http://www.recmath.com/PolyPages/PolyPages/Reptiles.htm.
• Weisstein, Eric W. Rep-Tile (англ.) на сайте Wolfram MathWorld.
• http://www.meden.demon.co.uk/Fractals/reptiles.html (2001)
• https://web.archive.org/web/20111027142835/http://www.uwgb.edu/dutchs/SYMMETRY/reptile1.htm (1999)

Irrep-плитки

• Math Magic — Problem of the Month 10/2002 Архивная копия от 9 декабря 2015 на Wayback Machine
• Tanya Khovanova — L-Irreptiles