Эксцесс (сферическая тригонометрия)
Эксцесс сферического треугольника, или сферический избыток, — величина в сферической тригонометрии, показывающая, насколько сумма углов сферического треугольника превышает развёрнутый угол.
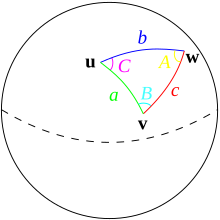
Определение
правитьОбозначим A, B, C радианные меры углов сферического треугольника. Тогда эксцесс
Свойства и вычисление
править- Поскольку в любом сферическом треугольнике, в отличие от треугольника на плоскости, сумма углов всегда больше π, то эксцесс всегда положителен. Сверху он ограничен числом 2π, то есть всегда меньше этого числа[1]:15.
- Для вычисления эксцесса сферического треугольника со сторонами a, b, c используется формула Люилье[1]:94:
- Для вычисления эксцесса сферического треугольника по сторонам a, b и углу C между ними используется формула[1]:95:
Применение
править- Эксцесс сферического треугольника применяется при вычислении его площади, поскольку (здесь — радиус сферы, на которой расположен сферический треугольник, а эксцесс выражен в радианах)[1]:99.
- Телесный угол трёхгранного угла выражается по теореме Люилье через его плоские углы при вершине, как:
- , где — полупериметр.
- Через двугранные углы телесный угол выражается, как:
Примечания
правитьСсылки
править- Сферический избыток — статья из Большой советской энциклопедии.
- Сферический избыток на сайте MathWorld