Хи-распределение — непрерывное вероятностное распределение случайной величины, являющейся квадратным корнем суммы квадратов независимых нормальных случайных величин. Оно связано с хи-квадрат распределением и является распределением квадратного корня случайной величины, распределённой по закону
χ
2
{\displaystyle \chi ^{2}}
Распределение хи Плотность вероятности Функция распределения
Параметры
k
>
0
{\displaystyle k>0\,}
Носитель
x
∈
[
0
,
∞
)
{\displaystyle x\in [0,\infty )}
Плотность вероятности
1
2
(
k
/
2
)
−
1
Γ
(
k
/
2
)
x
k
−
1
e
−
x
2
/
2
{\displaystyle {\frac {1}{2^{(k/2)-1}\Gamma (k/2)}}\;x^{k-1}e^{-x^{2}/2}}
Функция распределения
P
(
k
/
2
,
x
2
/
2
)
{\displaystyle P(k/2,x^{2}/2)\,}
Математическое ожидание
μ
=
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
{\displaystyle \mu ={\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}}
Медиана
примерно
k
(
1
−
2
9
k
)
3
{\displaystyle {\sqrt {k{\bigg (}1-{\frac {2}{9k}}{\bigg )}^{3}}}}
Мода
k
−
1
{\displaystyle {\sqrt {k-1}}\,}
k
≥
1
{\displaystyle k\geq 1}
Дисперсия
σ
2
=
k
−
μ
2
{\displaystyle \sigma ^{2}=k-\mu ^{2}\,}
Коэффициент асимметрии
γ
1
=
μ
σ
3
(
1
−
2
σ
2
)
{\displaystyle \gamma _{1}={\frac {\mu }{\sigma ^{3}}}\,(1-2\sigma ^{2})}
Коэффициент эксцесса
2
σ
2
(
1
−
μ
σ
γ
1
−
σ
2
)
{\displaystyle {\frac {2}{\sigma ^{2}}}(1-\mu \sigma \gamma _{1}-\sigma ^{2})}
Дифференциальная энтропия
ln
(
Γ
(
k
/
2
)
)
+
{\displaystyle \ln(\Gamma (k/2))+\,}
1
2
(
k
−
ln
(
2
)
−
(
k
−
1
)
ψ
0
(
k
/
2
)
)
{\displaystyle {\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi _{0}(k/2))}
Производящая функция моментов
См. в тексте
Характеристическая функция
См. в тексте
Если
Z
1
,
…
,
Z
k
{\displaystyle Z_{1},\ldots ,Z_{k}}
нормально распределёнными случайными величинами с нулевым математическим ожиданием (средним) и дисперсией равной 1, то статистика
Y
=
∑
i
=
1
k
Z
i
2
{\displaystyle Y={\sqrt {\sum _{i=1}^{k}Z_{i}^{2}}}}
распределена по закону хи. Соответственно, если оценку среднеквадратического отклонения
s
{\displaystyle s}
μ
1
/
n
−
1
{\displaystyle \mu _{1}/{\sqrt {n-1}}}
μ
1
{\displaystyle \mu _{1}}
k
{\displaystyle k}
степеней свободы (то eсть количество
Z
i
{\displaystyle Z_{i}}
Самые известные примеры — распределение Рэлея (число степеней свободы равно двум) и статистика Максвелла — Больцмана (число степеней свободы — три).
Плотность вероятности хи распределения равна
f
(
x
;
k
)
=
{
x
k
−
1
e
−
x
2
/
2
2
k
/
2
−
1
Γ
(
k
2
)
,
x
⩾
0
;
0
,
x
<
0.
{\displaystyle f(x;k)={\begin{cases}{\dfrac {x^{k-1}e^{-x^{2}/2}}{2^{k/2-1}\Gamma \left({\frac {k}{2}}\right)}},&x\geqslant 0;\\0,&x<0.\end{cases}}}
где
Γ
(
z
)
{\displaystyle \Gamma (z)}
гамма-функция .
Функция распределения равна:
F
(
x
;
k
)
=
P
(
k
/
2
,
x
2
/
2
)
{\displaystyle F(x;k)=P(k/2,x^{2}/2)\,}
где
P
(
k
,
x
)
{\displaystyle P(k,x)}
регуляризованная гамма-функция .
Производящая функция моментов равна:
M
(
t
)
=
M
(
k
2
,
1
2
,
t
2
2
)
+
t
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
M
(
k
+
1
2
,
3
2
,
t
2
2
)
,
{\displaystyle M(t)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {t^{2}}{2}}\right)+t{\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {t^{2}}{2}}\right),}
где
M
(
a
,
b
,
z
)
{\displaystyle M(a,b,z)}
гипергеометрическая функция Куммера. Характеристическая функция равна:
φ
(
t
;
k
)
=
M
(
k
2
,
1
2
,
−
t
2
2
)
+
i
t
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
M
(
k
+
1
2
,
3
2
,
−
t
2
2
)
.
{\displaystyle \varphi (t;k)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {-t^{2}}{2}}\right)+it{\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {-t^{2}}{2}}\right).}
Моменты вычисляются по формуле:
μ
j
=
2
j
/
2
Γ
(
(
k
+
j
)
/
2
)
Γ
(
k
/
2
)
{\displaystyle \mu _{j}=2^{j/2}{\frac {\Gamma ((k+j)/2)}{\Gamma (k/2)}}}
где
Γ
(
z
)
{\displaystyle \Gamma (z)}
гамма-функция . Первые шесть моментов задаются по следующим формулам:
μ
1
=
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
{\displaystyle \mu _{1}={\sqrt {2}}\,\,{\frac {\Gamma ((k\!+\!1)/2)}{\Gamma (k/2)}}}
μ
2
=
k
{\displaystyle \mu _{2}=k\,}
μ
3
=
2
2
Γ
(
(
k
+
3
)
/
2
)
Γ
(
k
/
2
)
=
(
k
+
1
)
μ
1
{\displaystyle \mu _{3}=2{\sqrt {2}}\,\,{\frac {\Gamma ((k\!+\!3)/2)}{\Gamma (k/2)}}=(k+1)\mu _{1}}
μ
4
=
k
(
k
+
2
)
{\displaystyle \mu _{4}=k(k+2)\,}
μ
5
=
4
2
Γ
(
(
k
+
5
)
/
2
)
Γ
(
k
/
2
)
=
(
k
+
1
)
(
k
+
3
)
μ
1
{\displaystyle \mu _{5}=4{\sqrt {2}}\,\,{\frac {\Gamma ((k\!+\!5)/2)}{\Gamma (k/2)}}=(k+1)(k+3)\mu _{1}}
μ
6
=
k
(
k
+
2
)
(
k
+
4
)
{\displaystyle \mu _{6}=k(k+2)(k+4)\,}
где правые выражения получены, используя рекуррентное соотношение для гамма-функции:
Γ
(
x
+
1
)
=
x
Γ
(
x
)
{\displaystyle \Gamma (x+1)=x\Gamma (x)\,}
Также из этих выражений можно получить следующие формулы:
Среднее :
μ
=
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
{\displaystyle \mu ={\sqrt {2}}\,\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}}
Дисперсия :
σ
2
=
k
−
μ
2
{\displaystyle \sigma ^{2}=k-\mu ^{2}\,}
Коэффициент асимметрии :
γ
1
=
μ
σ
3
(
1
−
2
σ
2
)
{\displaystyle \gamma _{1}={\frac {\mu }{\sigma ^{3}}}\,(1-2\sigma ^{2})}
Коэффициент эксцесса :
γ
2
=
2
σ
2
(
1
−
μ
σ
γ
1
−
σ
2
)
{\displaystyle \gamma _{2}={\frac {2}{\sigma ^{2}}}(1-\mu \sigma \gamma _{1}-\sigma ^{2})}
Дифференциальная энтропия задаётся по формуле:
S
=
ln
(
Γ
(
k
/
2
)
)
+
1
2
(
k
−
ln
(
2
)
−
(
k
−
1
)
ψ
0
(
k
/
2
)
)
{\displaystyle S=\ln(\Gamma (k/2))+{\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi ^{0}(k/2))}
где
ψ
0
(
z
)
{\displaystyle \psi ^{0}(z)}
полигамма-функция .
править
Если
X
∼
χ
k
{\displaystyle X\sim \chi _{k}}
X
2
∼
χ
k
2
{\displaystyle X^{2}\sim \chi _{k}^{2}}
хи-квадрат-распределение )
lim
k
→
∞
χ
k
−
μ
k
σ
k
→
d
N
(
0
,
1
)
{\displaystyle \lim _{k\to \infty }{\tfrac {\chi _{k}-\mu _{k}}{\sigma _{k}}}{\xrightarrow {d}}\ N(0,1)\,}
нормальное распределение )Если
X
∼
N
(
0
,
1
)
{\displaystyle X\sim N(0,1)\,}
|
X
|
∼
χ
1
{\displaystyle |X|\sim \chi _{1}\,}
Если
X
∼
χ
1
{\displaystyle X\sim \chi _{1}\,}
σ
X
∼
H
N
(
σ
)
{\displaystyle \sigma X\sim HN(\sigma )\,}
полунормальное распределение ) для любых
σ
>
0
{\displaystyle \sigma >0\,}
χ
2
∼
R
a
y
l
e
i
g
h
(
1
)
{\displaystyle \chi _{2}\sim \mathrm {Rayleigh} (1)\,}
распределение Рэлея )
χ
3
∼
M
a
x
w
e
l
l
(
1
)
{\displaystyle \chi _{3}\sim \mathrm {Maxwell} (1)\,}
распределение Максвелла )
‖
N
i
=
1
,
…
,
k
(
0
,
1
)
‖
2
∼
χ
k
{\displaystyle \|{\boldsymbol {N}}_{i=1,\ldots ,k}{(0,1)}\|_{2}\sim \chi _{k}}
вторая норма от
k
{\displaystyle k}
k
{\displaystyle k}
Хи-распределение — специальный случай гамма-распределения , распределение Накагами и нецентрального хи-распределения .
Виды распределений хи и хи-квадрат
Название
Статистика
хи-квадрат распределение
∑
i
=
1
k
(
X
i
−
μ
i
σ
i
)
2
{\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}
нецентральное хи-квадрат распределение
∑
i
=
1
k
(
X
i
σ
i
)
2
{\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}
хи-распределение
∑
i
=
1
k
(
X
i
−
μ
i
σ
i
)
2
{\displaystyle {\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}}
нецентральное хи-распределение
∑
i
=
1
k
(
X
i
σ
i
)
2
{\displaystyle {\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}}}
Martha L. Abell, James P. Braselton, John Arthur Rafter, John A. Rafter, Statistics with Mathematica (1999), 237f.
Jan W. Gooch, Encyclopedic Dictionary of Polymers vol. 1 (2010), Appendix E, p. 972 .  Плотность вероятности
Плотность вероятности 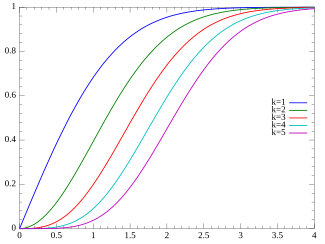 Функция распределения
Функция распределения 



















