Формула Эйлера (дифференциальная геометрия)
Формула Эйлера — формула, позволяющая вычислить нормальную кривизну поверхности.
Названа в честь Леонарда Эйлера, который доказал её в 1760 году.
Формулировка
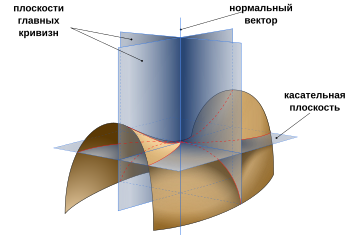
правитьПусть есть регулярная поверхность в трёхмерном евклидовом пространстве. Пусть — точка — касательная плоскость к в точке — единичная нормаль к в точке а — плоскость, проходящая через и некоторый единичный вектор в . Кривая получающаяся как пересечение плоскости с поверхностью называется нормальным сечением поверхности в точке в направлении Величина
где обозначает скалярное произведение, а — вектор кривизны в точке , называется нормальной кривизной поверхности в направлении . С точностью до знака нормальная кривизна равна кривизне кривой .
В касательной плоскости существуют два перпендикулярных направления и такие, что нормальную кривизну в произвольном направлении можно представить с помощью так называемой формулы Эйлера:
где — угол между этим направлением и , a величины и нормальные кривизны в направлениях и , они называются главными кривизнами, а направления и — главными направлениями поверхности в точке . Главные кривизны являются экстремальными значениями нормальных кривизн. Структуру нормальных кривизн в данной точке поверхности удобно графически изображать с помощью индикатрисы Дюпена.
См. также
правитьСсылки
править- Euler, Leonhard (1760), "Recherches sur la courbure des surfaces", Memoires de l'academie des sciences de Berlin, 16 (published 1767): 119–143.