Теория размещения производства
Теория размещения производства (теория локации) — учение размещения производственных сил на территории[1], является частью региональной экономики. Теория рассматривает вопросы, какая хозяйственная деятельность находится там, где и почему, и базируется на принципе, что фирмы выбирают месторасположения, которые будут максимизировать их прибыль, а частные лица выбирают те места, которые максимизируют их полезность.
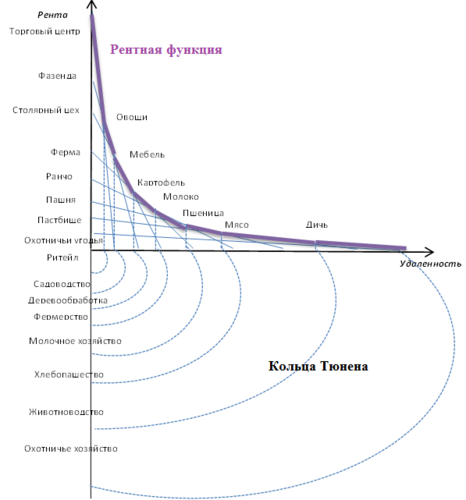
Теория сельскохозяйственного штандорта
правитьИсследования географического размещения экономической активности прослеживались в работах Ричарда Кантильона, Этьен Бонно де Кондильяк, Дэвида Юма, Джеймса Денем-Стюарта, Давида Рикардо. Уолтер Айзард считает, что создание модели Тюнена (теории сельскохозяйственного штандорта) в 1826 году послужило базисом теории по размещению производства[2].
Вильгельм Лаунхардт добавляет в модель Тюнена, имеющую свои допущения и принципы, дополнительную закономерность, что производство скоропортящихся, тяжелых и объемных продуктов будет располагаться вблизи города и формирует «Диаграмму модели Тюнена» в своей книге «Математическое обоснование учения о народном хозяйстве» от 1885 года. Данная диаграмма демонстрирует рентную функцию. По вертикали указывается стоимость земли на каждый вид участка в стоимостном выражении, а по горизонтали удаленность в километрах. Нижняя часть диаграммы образует кольца Тюнена, в которых располагаются производства, а в верхней правой части указываются продукты, производящие данными производствами. Расстояние между кольцами, разграничивающие посевы двух культур:
,
где m1 и m2 — доходность сельскохозяйственных культур на единицу продукции, v1 и v2 — объёмы производства культур, t — транспортный тариф на 1 т·км, r — расстояние от центра[1].
Рациональный штандорт промышленного предприятия (модель Лаунхардта)
правитьВ. Лаунхардт представил свою модель в работе «Практика эффективного размещения предприятий»[3] от 1882 года как задачу размещения производства (проблема трех точек), где производится один вид продукции, удельные издержки постоянны, существует один рынок сбыта, источник сырья и источник материалов. Оптимальным местом размещения будет то, где транспортные издержки на единицу продукции минимальны: минимальны по доставке сырья и пунктом реализации. Точка оптимального размещения предприятия находится в зависимости от весовых соотношений перевозимых грузов и расстояний. Задача решается методом Локационного треугольника, который имеет геометрический метод нахождения точки размещения: на каждой из сторон локационного треугольника строится треугольник, подобный весовому. Затем вокруг построенных таким образом треугольников описываются окружности, точка пересечения которых и является точкой минимума транспортных издержек[4]:
- → ,
где T — стоимость перевозки, Х и Y — вес сырья и материалов, требуемого для производства единицы конечного продукта, Z — вес конечного продукта, AM, BM, CM — расстояние от внутренней точки М (места расположения завода) до вершин треугольника.
Каждая вершина треугольника тянет к себе производство с силой, пропорциональной весу, который нужно из неё возить, что совпадает с одним из устройств французского математика Пьера Вариньона, где происходит минимизация суммарной потенциальной энергии системы грузов с массами, равными перемещаемым грузам[4].
Теория промышленного штандорта
правитьАльфред Вебер предложил в своей работе от 1909 года дополнить модель Лаунхардта (где затраты на труд в любой точке были одинаковы) минимизацией общих издержек производства, зависящих от местоположения: транспортные издержки; издержки на рабочую силу; издержки на сырье и материалы. Транспортные издержки зависят от массы перевозимых грузов и расстояния перевозки. Промышленные предприятия будут притягиваться к тому месту, в котором имеют место минимальные величины транспортных издержек. Производства с высоким индексом материалоемкости (отношения веса локализованных материалов, то есть которые можно получить только из уникальных источников, к весу готового продукта) тяготеют к местам производства сырья и материалов, а с небольшим индексом к пункту потребления[1].
Места с низкими расходами на рабочую силу на единицу продукции будут притягивать к себе производства до тех пор, пока экономия на зарплате в данном месте будет перекрывать перерасход в транспортных издержках из-за перемещения производства. Приросты транспортных издержек в связи с перемещением производства увеличиваются с удалением от транспортного пункта равномерно в любом направлении удаления. Линии, соединяющие эти пункты аналогичных издержек отклонения, называется изодапанами[1].
Агломерация происходит за счет экономии на масштабах производства, наличия удобных рынков сбыта, близости вспомогательных отраслей и более дешевой рабочей силы способствует концентрации промышленных предприятий в городских центрах. А дегломерация (рост земельной ренты в перенаселенных центрах, повышение уровня зарплаты, рост цен на материалы) противостоит централизации. Когда экономия затрат от агломерации выше дополнительных издержек на транспорт и рабочую силу, возрастающие вследствие перемещения промышленности в пункты агломерации, происходит отклонение центров производства от оптимальных пунктов по транспортной и рабочей ориентации. Графически эта задача решается при помощи изодапан (изолиний равных издержек на рисунке «Изодапаны транспортных издержек модели Вебера» это А1, А2, А3, А4) проводимых вокруг оптимальных пунктов транспортной ориентации (на рисунке «Изодапаны транспортных издержек модели Вебера» это Р) и соединяющие точки аналогичных отклонений в транспортных издержках при перемещении производства в рабочие узлы (L1 или L2). Изодапана по точкам, в которых отклонения транспортных издержек равны экономии на зарплате, называется критической изодапаной для данного рабочего пункта. Когда рабочий пункт лежит внутри своей критической изодапаны, то перемещение производства из транспортного в рабочий пункт выгодно, если вне её, то перемещение невыгодно[1].
Место, где издержки отклонения для каждого производства не превышают выгоды, получаемой от агломерации, показаны заштрихованной площадью общего сегмента (на рисунке «Агломерация модели Вебера» Р1, Р2, Р3 — пункты транспортного минимума). Агломерируемые производства размещаются в заштрихованном сегменте, а сама точка размещения внутри сегмента находится с учетом транспортного фактора[1]. Второе геометрическое решение данной задачи Вебера может быть представлено с помощью точки Ферма.
А. Вебер также находит формулу агломерации[4]:
- ,
где f(M) — функция агломерации, выражающая притягательную силу крупного производства по отношению к рассеянным мелким производствам, M — производственная масса крупного производства, притягиваемая к агломерационному центру, А — штандортный вес, S − ставка транспортного тарифа (ткм), p — производственная плотность (объем продукции, приходящейся на единицу площади с радиусом R, при равномерном распределении производства на данной площади.
См. также
правитьПримечания
править- ↑ 1 2 3 4 5 6 Гранберг А. Г. Основы региональной экономики. — М.: ГУ ВШЭ, 2000. — С. 14, 40-51. — 495 с. — ISBN 5-7598-0074-4.
- ↑ Блауг М. Экономическая теория использования пространства и классическая теория размещения производства Архивная копия от 21 января 2022 на Wayback Machine // Экономическая мысль в ретроспективе. — М.: Дело, 1994. — С. 568-585. — ISBN 5-86461-151-4
- ↑ Launhardt W. Die Bestimmung des zweckmässigsten Standortes einer gewerblichen Anlage Архивная копия от 18 апреля 2018 на Wayback Machine// Zeitschrift des Vereines deutscher Ingenieure. v.26 (Mar), 1882 pp. 106—115
- ↑ 1 2 3 Лимонов Л. Э. Региональная экономика и пространственное развитие. — М.: Юрайт, 2015. — Т. 1. — С. 71-73. — ISBN 978-5-9916-4444-0. Архивировано 27 января 2017 года.
Эта статья входит в число добротных статей русскоязычного раздела Википедии. |