Теорема Штейнера — Лемуса

Теорема Штейнера — Лемуса — теорема геометрии треугольника. Известна как пример с виду простого утверждения, который не имеет простого классического доказательства, хотя есть несложное аналитическое доказательство.

$|AE|=|BD|,\,\alpha =\beta ,\,\gamma =\delta$

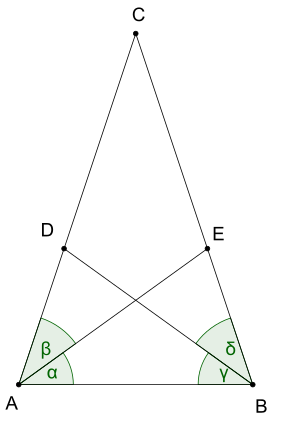
Формулировка

Если в треугольнике равны 2 биссектрисы, то этот треугольник является равнобедренным.

История доказательства

Доказательство было дано в работах немецких геометров Якоба Штейнера и Даниэля Лемуса в XIX веке.

В 1963 году журнал American Mathematical Monthly объявил конкурс на лучшее доказательство теоремы. Было прислано много доказательств, среди которых обнаружились интересные и ранее неизвестные. Одно из лучших, по мнению редакции, использует метод от противного и окружность, проходящую через 4 точки как дополнительное построение.

В советской литературе распространено доказательство, основанное на следующем признаке равенства треугольников: если угол, биссектриса этого угла и сторона, противолежащая этому углу, одного треугольника равны соответствующим элементам другого треугольника, то такие треугольники равны.

Аналитическое доказательство следует из формулы на длину биссектрисы

$l_{c}={\frac {\sqrt {4abp(p-c)}}{a+b}}.$

Вариации и обобщения

• Аналогичная теорема для биссектрис внешних углов (отрезков биссектрис внешних углов, проведенных до продолжения сторон) неверна. Один из контрпримеров — треугольник Боттема — с углами 12°, 132° и 36°. В нём отрезки биссектрис, внешних к первым двум углам, проведённых до пересечения с продолжениями сторон, равны стороне, соединяющей их вершины.

Литература

• Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 335-338. — 383 с. — ISBN 5-09-001287-3.
• Понарин Яков Петрович. Элементарная геометрия. В 2 [3] тт. Ред. Семёнов А.В. — М.: МЦНМО, 2004 (том 1), 2006 (том 2), 2009 (том 3). — 312+256+192 стр. — ISBN 978-5-94057-397-5, 978-5-94057-170-0 (все тома), 978-5-94057-171-9 (том 1), 978-5-94057-223-5 (том 2), 978-5-94057-400-2 (том 3). По данной теореме см. т. 1, стр. 31-32.
• Weisstein, Eric W. Steiner–Lehmus theorem (англ.) на сайте Wolfram MathWorld.
• Несколько доказательств теоремы Штейнера — Лемуса (англ.)