Стержень Витгенштейна
Сте́ржень Витгенште́йна — геометрическая задача, поставленная философом XX века Людвигом Витгенштейном[1].
- Постановка задачи
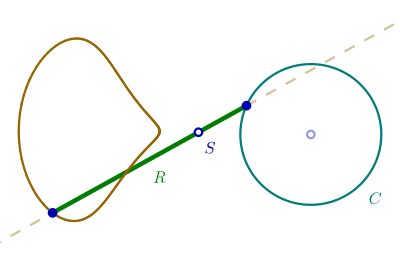
Постановка задачи такова. Открытая с двух сторон гильза шарнирно прикреплена к стене одной из своих образующих, причём гильза может свободно поворачиваться вокруг места крепления. Сквозь гильзу продет стержень, который может легко двигаться вдоль гильзы. Один конец стержня описывает на стене окружность.
- Вопрос
Вопрос мысленного эксперимента такой: какую траекторию будет описывать второй конец стержня?
Может показаться, что второй конец стержня тоже должен описывать окружность, однако на самом деле, он будет описывать инверсированную кардиоиду.
Форма, габариты, области существования и определения траектории стержня Витгенштейна могут быть разными — в зависимости от длины стержня R, радиуса окружности C, координат её центра, координат положения шарнира S, начальных координат свободного конца стержня.
Данная математическая конструкция применяется для облегчения понимания физических расчётов сингулярных процессов и процессов, вызванных инерционностью физических систем. Применение именно этой математической абстракции обычно объясняется сущностью инерции (тем, что она такое): у вектора, по инерции, сохраняется не только величина, но и направление (в шарнирную точку); и существованием радиуса кривизны пространства.
Форму траектории стержня Витгенштейна принимают языки пламени, падающие капли воды, загнутый пополам лист бумаги, если зажать между двух пальцев его сведённые вместе края, листья некоторых растений. А также графики зависимостей многих физических процессов (например, зависимость скорости движения лодки по воде после броска яблока из неё, от времени движения: разгон — торможение; или зависимости напряжения и силы тока от длины проводника замкнутой цепи только из подводящих ток проводов, без резистора — короткое замыкание; зависимость (от времени) интенсивности вторичного свечения атома при поглощении фотона).
Анимация
править-
Каплевидная форма
-
Точка крепления близка к окружности
-
Точка практически лежит на окружности
-
Точка внутри окружности
- ↑ Wittgenstein L., Remarks on the Foundations of Mathematics, edited by G.H. von Wright and Rush Rhees, Oxford: Blackwell 1998, ISBN 0-631-12505-1, sect V, § 72, p.434
Ссылки
правитьЭто заготовка статьи по математике. Помогите Википедии, дополнив её. |