Редко используемые тригонометрические функции — функции угла, которые в настоящее время используются редко по сравнению с шестью основными тригонометрическими функциями (синусом, косинусом, тангенсом, котангенсом, секансом и косекансом). К ним относятся:
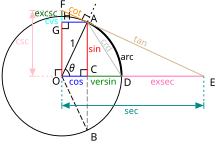

- Синус-верзус (другие написания: версинус, синус версус, называется также «стрелка дуги»). Определяется как Представляет собой расстояние от центральной точки дуги, измеряемой удвоенным данным углом, до центральной точки хорды, стягивающей дугу. Иногда используются обозначения
- Косинус-верзус (другие написания: косинус версус или веркосинус). Определяется как Иногда используются обозначения cos vers.
- Аккорд — одна из редких тригонометрических функций, которая использовалась в ранней тригонометрии. Определяется эта функция как 2sin(x/2).
- Коверсинус (лат. coversinus, сокращение от coversed sine. Другие написания: синус-коверзус, покрытый синус.) Определяется эта функция как . Для этой функции используются также обозначения или .
- Коверкосинус (лат. covercosinus, сокращение от covercosed sinе. Другие написания: косинус-коверзус, покрытый косинус.) Определяется функция как . Для данной функции также используeтся обозначениe .
- Гаковерсинус (лат. hacoversinus, coкращение от half the coversed sine.) Определяется данная функция как .
- Гаковеркосинус (лат. hacovercosinus, сокращение от half the covercosed sine.) Определяется как .
- Гаверсинус (лат. haversinus, сокращение от half the versed sine). Определяется как Используется также обозначение
- Гаверкосинус (лат. havercosinus, сокращение от half the versed cosine). Определяется как Используется также обозначение
- Эксеканс (лат. exsecant) или экссеканс. Определяется как
- Экскосеканс — дополнительная функция к эксекансу:
Использование
правитьВерсинус, коверсинус и гаверсинус были удобны для ручных расчётов с использованием логарифмов (использовали логарифмы или логарифмическую линейку), поскольку они всюду неотрицательны, однако в связи с развитием вычислительных средств эта область применения неактуальна. В настоящее время эти функции используются для описания соответствующих сигналов в электронике (например, в функциональных генераторах). Гаверсинус также используется в навигационных расчётах для избежания ошибок округления в вычислительных системах с ограниченной разрядностью. Гаверсинус используется в формуле Хаверсина также для навигационных расчётах.
Функция эксеканс использовалась в железнодорожном строительстве, сферической тригонометрии, а также в геодезии вплоть до 1980-х годов. Экскосеканс использовался в кинетической энергии фермионов знаменитым физиком Альбертом Эйнштейном.
Синус-верзус
правитьОпределение
правитьСинус-верзус определён через синус и косинус как
Синус-верзус вместе с косинусом составляет радиус окружности.
Свойства
правитьВерсинус — периодическая функция с периодом . Версинус определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.
можно использовать в плоскости комплексных чисел.
Производная версинуса
правитьПервообразная версинуса
правитьКосинус-верзус
правитьОпределение
правитьКосинус-верзус определён через версинус и косинус как
Свойства
правитьВеркосинус — периодическая функция с периодом . Веркосинус определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.
можно использовать в плоскости комплексных чисел.
Производная веркосинуса
правитьПервообразная веркосинуса
правитьГаверсинус
правитьОпределение
правитьГаверсинус определён через верзус-синус и синус как
Свойства
правитьГаверсинус — периодическая функция с периодом . Гаверсинус определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.
можно использовать в плоскости комплексных чисел.
Производная гаверсинуса
правитьПервообразная гаверсинуса
правитьГаверкосинус
правитьОпределение
правитьГаверкосинус определён через верзус-косинус и косинус как
Свойства
правитьГаверкосинус — периодическая функция с периодом . Гаверкосинус определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.
можно использовать в плоскости комплексных чисел.
Производная гаверкосинуса
правитьПервообразная гаверкосинуса
правитьЭксеканс
правитьОпределение
правитьЭксеканс определён через секанс как
- Эксеканс можно определить через тангенс и синус-верзус как
- exsec(x) = versin(x)/cos(x)
- exsec(x) = tg(x)*tg(x/2)
Свойства
правитьЭксеканс — периодическая функция с периодом . Эксеканс определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.
можно использовать в плоскости комплексных чисел.
Производная эксеканса
править
Первообразная эксеканса
правитьЭкскосеканс
правитьОпределение
правитьЭкскосеканс определён через эксеканс и косеканс как
Свойства
правитьЭкскосеканс — периодическая функция с периодом . Экскосеканс определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.
можно использовать в плоскости комплексных чисел.















