Радужная таблица

Радужная таблица (англ. rainbow table) — специальный вариант таблиц поиска (англ. lookup table) для обращения криптографических хеш-функций, использующий механизм разумного компромисса между временем поиска по таблице и занимаемой памятью (англ. time-memory tradeoff).

Радужные таблицы используются для вскрытия паролей, преобразованных при помощи сложнообратимой хеш-функции, а также для атак на симметричные шифры на основе известного открытого текста.

Использование функции формирования ключа с применением соли делает эту атаку неосуществимой.
Радужные таблицы являются развитием более раннего и простого алгоритма, предложенного Мартином Хеллманом^[1].

Предпосылки к появлению

Компьютерные системы, которые используют пароли для аутентификации, должны каким-то образом определять правильность введённого пароля. Самым простым способом решения данной проблемы является хранение списка всех допустимых паролей для каждого пользователя. Минусом данного метода является то, что в случае несанкционированного доступа к списку злоумышленник узнаёт все пользовательские пароли. Более распространённый подход заключается в хранении значений криптографической хеш-функции от парольной фразы. Однако большинство хешей быстро вычисляется, поэтому злоумышленник, получивший доступ к хешам, может быстро проверить список возможных паролей на валидность. Чтобы избежать этого, нужно использовать более длинные пароли, тем самым увеличивая список паролей, которые должен проверить злоумышленник. Для простых паролей, не содержащих соли, взломщик может заранее подсчитать значения хешей для всех распространённых и коротких паролей и сохранить их в таблице. Теперь можно быстро найти совпадение в заранее полученной таблице. Но чем длиннее пароль, тем больше таблица, и тем больше памяти необходимо для её хранения. Альтернативным вариантом является хранение только первых элементов цепочек хешей. Это потребует больше вычислений для поиска пароля, но значительно уменьшит количество требуемой памяти. А радужные таблицы являются улучшенным вариантом данного метода, которые позволяют избежать коллизий.

Предрассчитанные цепочки хешей

Хеширование - это преобразование входного массива данных произвольной длины в выходную битовую строку фиксированной длины. Его используют в:

Зачастую хеш-функции используются для:

• построения ассоциативных массивов;

• поиска дубликатов в наборе данных;

• создания уникальных идентификаторов;

• вычисления контрольных сумм;

• хранения паролей в защищённом виде;

• создания электронной подписи.

Криптографические хэш-верификаторы считаются безопасными и используются для проверки целостности и подлинности. Таким образом, высокая алгоритмическая сложность и однонаправленность послужили основанием для легитимности электронных подписей и их аналогов в системах информационной безопасности. Существует 4 основных направления шифрования информации::

1. симметричное;

2. ассиметричное;

3. хеширование;

4. беспроводное.

Цепочки хешей, описанные в этой статье, отличаются от описанных в статье Цепочка хешей.

Предположим, у нас есть хэш-функция H с длиной хэша n и конечное множество паролей P. Наша цель - создать структуру данных, которая для любого значения хэша h может либо найти элемент p из P такой, что H(p)=h, либо определить, что такого элемента не существует. Самый простой способ сделать это - вычислить H(p) для всех p из P, но для хранения такой таблицы потребуется Θ(|P|n) памяти, что слишком много.

Хэш-цепочки - это метод, позволяющий сократить потребность в памяти. Основная идея заключается в определении редукционной функции R, которая отображает значения из P в хэш-значения. Обратите внимание, что R не является инверсией хэш-функции. Начиная с исходного пароля и поочередно применяя H и R к каждому полученному значению, мы получим цепочку чередующихся паролей и хэшей. Например, для набора паролей из 6 символов и хэш-функции, выдающей 32-битные значения, цепочка может выглядеть следующим образом:

\mathbf {aaaaaa} \,{\xrightarrow[{\;H\;}]{}}\,\mathrm {281DAF40} \,{\xrightarrow[{\;R\;}]{}}\,\mathrm {sgfnyd} \,{\xrightarrow[{\;H\;}]{}}\,\mathrm {920ECF10} \,{\xrightarrow[{\;R\;}]{}}\,\mathbf {kiebgt}

К функции редукции предъявляется единственное требование: возвращать значения из того же алфавита, что и пароли.

Для создания таблицы мы выбираем случайный набор начальных паролей из P, вычисляем цепочки фиксированной длины k для каждого пароля и сохраняем только первый и последний пароль из каждой цепочки.

Для каждого хэша h, значение которого мы хотим обратить (найти соответствующий ему пароль), мы вычисляем последовательность R(...R(H(R(h)))...). Если какое-то из промежуточных значений совпадает с концом некоторой цепочки, то берем начало этой цепочки и восстанавливаем ее полностью. С большой вероятностью полная цепочка будет содержать хэш-значение h, а предшествующий ему пароль будет тем, который мы ищем.

Для примера, указанного выше, если у нас изначально есть хеш 920ECF10, он породит следующую последовательность:

\mathrm {920ECF10} \,{\xrightarrow[{\;R\;}]{}}\,\mathbf {kiebgt}

Поскольку kiebgt - это конец цепочки из нашей таблицы, мы берем соответствующий начальный пароль aaaaaa и вычисляем цепочку, пока не найдем хэш 920ECF10:

\mathbf {aaaaaa} \,{\xrightarrow[{\;H\;}]{}}\,\mathrm {281DAF40} \,{\xrightarrow[{\;R\;}]{}}\,\mathrm {sgfnyd} \,{\xrightarrow[{\;H\;}]{}}\,\mathrm {920ECF10}

Таким образом, искомый пароль — sgfnyd.

Следует отметить, что восстановленная цепочка не всегда содержит искомое значение хэша h. Это возможно в случае коллизии функций H или R. Например, пусть дан хэш FB107E70, который на определенном этапе генерирует пароль kiebgt:

\mathrm {FB107E70} \,{\xrightarrow[{\;R\;}]{}}\,\mathrm {bvtdll} \,{\xrightarrow[{\;H\;}]{}}\,\mathrm {0EE80890} \,{\xrightarrow[{\;R\;}]{}}\,\mathbf {kiebgt}

Но FB107E70 не появляется в цепочке, сгенерированной паролем aaaaa. Это называется ложным срабатыванием. В этом случае мы игнорируем совпадение и продолжаем вычислять последовательность, сгенерированную h. Если сгенерированная последовательность достигает длины k без каких-либо хороших совпадений, это означает, что искомый пароль никогда не появлялся в предварительно вычисленных цепочках.

Содержимое таблицы не зависит от обратного хэш-значения, оно вычисляется заранее и используется только для быстрого поиска. Увеличение длины цепочки уменьшает размер таблицы, но увеличивает время поиска нужного элемента в цепочке.

Простые хэш-цепочки имеют несколько недостатков. Самый серьезный из них - возможность слияния двух цепочек в одну (генерация одного и того же значения в разных цепочках). Все значения, сгенерированные после слияния, будут одинаковыми в обеих цепочках, что сужает количество охватываемых паролей. Поскольку предварительно сгенерированные цепочки не хранятся целиком, невозможно эффективно сравнить все сгенерированные значения друг с другом. Как правило, о бесколлизионной хэш-функции H заботится сторона, обеспечивающая шифрование паролей, поэтому основная проблема заключается в функции сокращения R.

Другой серьезной проблемой является выбор такой функции R, которая будет генерировать пароли с требуемым покрытием и распределением. Серьезным ограничением при выборе такой функции является ограничение на выходной алфавит.

Радужные таблицы

Радужные таблицы являются развитием идеи таблицы хеш-цепочек. Они эффективно решают проблему коллизий путём введения последовательности функций редукции R₁, R₂, …, R_k. Функции редукции применяются по очереди, перемежаясь с функцией хеширования: H, R₁, H, R₂, …, H, R_k. При таком подходе две цепочки могут слиться только при совпадении значений на одной и той же итерации. Следовательно, достаточно проверять на коллизии только конечные значения цепочек, что не требует дополнительной памяти. На конечном этапе составления таблицы можно найти все слившиеся цепочки, оставить из них только одну и сгенерировать новые, чтобы заполнить таблицу необходимым количеством различных цепочек. Полученные цепочки не являются полностью свободными от коллизий, тем не менее, они не сольются полностью.

Использование последовательностей функций редукции изменяет способ поиска по таблице. Поскольку хеш может быть найден в любом месте цепочки, необходимо сгенерировать k различных цепочек:

первая цепочка строится в предположении, что искомый хеш встретится на последней позиции в табличной цепочке, поэтому состоит из единственного значения R_k(h);
вторая цепочка строится в предположении, что искомый хеш встретится на предпоследней позиции в табличной цепочке, поэтому выглядит так: R_k(H(R_k−1(h)));
аналогично, наращивая длину цепочки и применяя функции редукции с меньшими номерами, получаем остальные цепочки. Последняя цепочка будет иметь длину k и содержать все функции редукции: R_k(H(R_k−1(H(…H(R₁(h))…))))

Также изменится и определение ложного срабатывания: если мы неверно «угадаем» позицию искомого хеша, это будет отбрасывать только одну из k сгенерированных цепочек; при этом всё ещё может оставаться возможность найти верный хеш для данной табличной цепочки, но на другой позиции.

Хотя радужные таблицы требуют отслеживания большего количества цепочек, они имеют бо́льшую плотность количества паролей на одну табличную запись. В отличие от таблицы хеш-цепочек, применение нескольких функций редукции уменьшает число потенциальных коллизий в таблице, что позволяет её наращивать без опасности получить большое количество слияний цепочек.

Пример

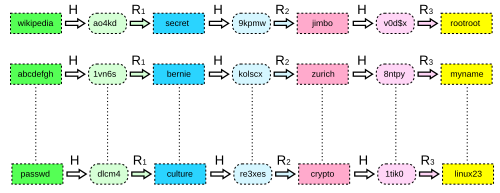
Имеется хеш (re3xes), который надо обратить (восстановить соответствующий пароль), и радужная таблица, полученная с использованием трёх функций редукции.

Вычисляем цепочку длины 1 от начального хеша: R₃(«re3xes»)="rambo". Данный пароль не является концом ни одной табличной цепочки.
Вычисляем цепочку длины 2: R₃(H(R₂(«re3xes»)))="linux23".
Данный пароль найден в таблице. Берём начало найденной цепочки (пароль passwd).
Восстанавливаем табличную цепочку до тех пор, пока не получим исходный хеш re3xes.
Искомый хеш найден в цепочке, атака успешна. Предшествующий данному значению хеша пароль culture является искомым.

Время и память

Радужная таблица создаётся построением цепочек возможных паролей. Создание таких таблиц требует больше времени, чем нужно для создания обычных таблиц поиска, но значительно меньше памяти (вплоть до сотен гигабайт, при объёме для обычных таблиц в N слов для радужных нужно всего порядка N^2/3). При этом они требуют хоть и больше времени (по сравнению с простыми методами вроде атаки по словарю) на восстановление исходного пароля, но на практике более реализуемы (для построения обычной таблицы для 6-символьного пароля с байтовыми символами потребуется 256⁶ = 281 474 976 710 656 блоков памяти, в то время как для радужной — всего 256^6·⅔ = 4 294 967 296 блоков).

Таблицы могут взламывать только ту хеш-функцию, для которой они создавались, то есть таблицы для MD5 могут взломать только хеш MD5. Теория данной технологии была разработана Philippe Oechslin^[2] как быстрый вариант time-memory tradeoff^[3]. Впервые технология использована в программе Ophcrack для взлома хешей LanMan (LM-хеш), используемых в Microsoft Windows. Позже была разработана более совершенная программа RainbowCrack, которая может работать с большим количеством хешей, например, LanMan, MD5, SHA1 и другими.

Следующим шагом было создание программы The UDC, которая позволяет строить Hybrid Rainbow таблицы не по набору символов, а по набору словарей, что позволяет восстанавливать более длинные пароли (фактически неограниченной длины).

Применение

При генерации таблиц важно найти наилучшее соотношения взаимосвязанных параметров:

вероятность нахождения пароля по полученным таблицам;
времени генерации таблиц;
время подбора пароля по таблицам;
занимаемое место.

Вышеназванные параметры зависят от настроек заданных при генерации таблиц:

допустимый набор символов;
длина пароля;
длина цепочки;
количество таблиц.

При этом время генерации зависит почти исключительно от желаемой вероятности подбора, используемого набора символов и длины пароля. Занимаемое таблицами место зависит от желаемой скорости подбора 1 пароля по готовым таблицам.

Хотя применение радужных таблиц облегчает использование полного перебора (то есть метода грубой силы — bruteforce) для подбора паролей, в некоторых случаях необходимые для их генерации/использования вычислительные мощности не позволяют одиночному пользователю достичь желаемых результатов за приемлемое время. К примеру, для паролей длиной не более 8 символов, состоящих из букв, цифр и специальных символов !@#$%^&*()-_+=, захешированных алгоритмом MD5, могут быть сгенерированы таблицы со следующими параметрами:

длина цепочки — 1400
количество цепочек — 50 000 000
количество таблиц — 800

При этом вероятность нахождения пароля с помощью данных таблиц составит 0,7542 (75,42 %), сами таблицы займут 596 ГиБ, генерация их на компьютере уровня Пентиум-3 1 ГГц займёт 3 года, а поиск 1 пароля по готовым таблицам — не более 22 минут.

Однако процесс генерации таблиц возможно распараллелить, например, расчёт одной таблицы с вышеприведёнными параметрами занимает примерно 33 часа. В таком случае, если в нашем распоряжении есть 100 компьютеров, все таблицы можно сгенерировать через 11 суток.

Защита от радужных таблиц

Один из распространённых методов защиты от взлома с помощью радужных таблиц — использование необратимых хеш-функций, которые включают salt («соль», «модификатор»). Существует множество возможных схем смешения затравки и пароля. Например, рассмотрим следующую функцию для создания хеша от пароля:

хеш = MD5( пароль + соль )

Для восстановления такого пароля взломщику необходимы таблицы для всех возможных значений соли. При использовании такой схемы, соль должна быть достаточно длинной (6‒8 символов), иначе злоумышленник может вычислить таблицы для каждого значения соли, случайной и различной для каждого пароля. Таким образом два одинаковых пароля будут иметь разные значения хешей, если только не будет использоваться одинаковая соль.

По сути, соль увеличивает длину и, возможно, сложность пароля. Если таблица рассчитана на некоторую длину или на некоторый ограниченный набор символов, то соль может предотвратить восстановление пароля. Например, в старых Unix-паролях использовалась соль, размер которой составлял всего лишь 12 бит. Для взлома таких паролей злоумышленнику нужно было посчитать всего 4096 таблиц, которые можно свободно хранить на терабайтных жёстких дисках. Поэтому в современных приложениях стараются использовать более длинную соль. Например, в алгоритме хеширования bcrypt используется соль размером 128 бит^[4]. Подобная длина соли делает предварительные вычисления просто бессмысленными. Другим возможным способом борьбы против атак, использующих предварительные вычисления, является растяжение ключа (англ. key stretching). Например:

ключ = хеш(пароль + соль)
for 1 to 65536 do
ключ = хеш(ключ + пароль + соль)

Этот способ снижает эффективность применения предварительных вычислений, так как использование промежуточных значений увеличивает время, которое необходимо для вычисления одного пароля, и тем самым уменьшает количество вычислений, которые злоумышленник может произвести в установленные временные рамки^[5] Данный метод применяется в следующих алгоритмах хеширования: MD5, в котором используется 1000 повторений, и bcrypt.^[6]. Альтернативным вариантом является использование усиления ключа (англ. key strengthening), который часто принимают за растяжение ключа. Применяя данный метод, мы увеличиваем размер ключа за счёт добавки случайной соли, которая затем спокойно удаляется, в отличие от растяжения ключа, когда соль сохраняется и используется в следующих итерациях^[7].

Предположим, что нам необходимо вычислить хеш-функцию пользователя с идентификатором user1 и паролем usergo. Алгоритм MD5 воспримет данные как запись user1usergo и рассчитает хеш-функцию – ca8881d70b2dc12c16204c782de1c5d. Учитывая, что рассмотренная комбинация является «словарной», программа RainbowCrack «взломает» такую хешфункция за несколько минут. Добавление «соли» 5hr8Uh32Hr приведет к следующей хеш-функции – e8ed0e735eb76ca4aeb0ca82891f1b06. Так как «соль» представляет собой набор случайных символов, использование Rainbow-метода и методов перебора становится невозможным. [1]

Использование

Практически все дистрибутивы ОС Unix, GNU/Linux и BSD используют хеши с солью для хранения системных паролей, хотя многие приложения, например, интернет-скрипты, используют простой хеш (обычно MD5) без «соли». ОС Microsoft Windows и Windows NT используют хеши LM-хеш и NTLM, которые также не используют «соль», что делает их самыми популярными для создания радужных таблиц.

Существует множество криптографических атак, и для того, чтобы хеш-функция была устойчивой, необходимо применять блочные шифры.

Использование на основе хэш-функций приложений позволит автоматизировать процессы: шифрования, электронно-цифровой подписи сразу нескольких документов.

Значительно повысится эффективность работы и снизится процент ошибок в процессе обработки электронных документов. Использование шифрования с ГОСТ алгоритмом позволяет передавать по открытым каналам связи информацию, содержащую коммерческую тайну, так же возможно сокрытия в зашифрованные архивы особо важную информацию, тем самым ограничив доступ к ней строго определённому кругу лиц.

Хеш-функции применяют в сетевых протоколах, алгоритмах электронно-цифровой подписи, механизмах аутентификации на основе паролей. Наиболее распространенной является последовательность хеш-функций MD2, MD4 и MD5. Все они генерируют результат работы хеш-функции фиксированной длины в 16 байт. [3]

Примечания

↑ Hellman M. A cryptanalytic time-memory trade-off // IEEE Transactions on Information Theory. — 1980. — Июль (т. 26, № 4). — С. 401—406. — ISSN 0018-9448. — doi:10.1109/TIT.1980.1056220. [исправить]
↑ Philippe Oechslin (неопр.). Дата обращения: 28 августа 2006. Архивировано 23 ноября 2005 года.
↑ Доклад Philippe Oechslin на конференции CRYPTO’03 Архивная копия от 26 сентября 2007 на Wayback Machine (PDF)
↑ Alexander, Steven. Password Protection for Modern Operating Systems (англ.) // ;login:. — USENIX Association, 2004. — June (vol. 29, no. 3). Архивировано 11 марта 2016 года.
↑ Ferguson, Neils; Bruce Schneier. Practical Cryptography (англ.). — Indianapolis: John Wiley & Sons, 2003. — ISBN 0-471-22357-3.
↑ Provos, Niels^[англ.]; Mazières, David^[англ.]. A Future-Adaptable Password Scheme (неопр.) // Proceedings of the FREENIX Track: 1999 USENIX Annual Technical Conference. — Monterey, CA, USA: USENIX Association, 1999. — 6 June. Архивировано 19 января 2012 года.
↑ U. Manber, "A Simple Scheme to Make Passwords Based on One-Way Functions Much Harder to Crack, " Computers & Security, v.15, n.2, 1996, pp.171-176. (англ.)

Литература

Все методы взлома MD5 [Электронный ресурс] URL. https://xakep.ru/2013/10/13/md5-hack/#toc14.
Борисов М.А. – «Основы программно-аппаратной защиты информации», издательство ЛЕНАНД, 2014 г.
Баскаков И.В., Евсеев В.Л. – «Защита информации в информационных системах», издательство Москва: Рудомино, 2011 г.

Ссылки

Страница Ophcrack Оригинальная исследовательская работа с демонстрацией
Проект RainbowCrack
oxid.it Содержит winrtgen — графическую оболочку для rtgen (утилиты создания таблиц)
Создание радужных таблиц для A5/1 (используется в GSM сетях, пока только для видеокарт с CUDA)
Большие радужные таблицы от группы Shmoo Group, создателей AirSnort

[1] Hellman M. A cryptanalytic time-memory trade-off // IEEE Transactions on Information Theory. — 1980. — Июль (т. 26, № 4). — С. 401—406. — ISSN 0018-9448. — doi:10.1109/TIT.1980.1056220. [исправить]

[2] Philippe Oechslin (неопр.). Дата обращения: 28 августа 2006. Архивировано 23 ноября 2005 года.

[3] Доклад Philippe Oechslin на конференции CRYPTO’03 Архивная копия от 26 сентября 2007 на Wayback Machine (PDF)

[alexander-4] Alexander, Steven. Password Protection for Modern Operating Systems (англ.) // ;login:. — USENIX Association, 2004. — June (vol. 29, no. 3). Архивировано 11 марта 2016 года.

[5] Ferguson, Neils; Bruce Schneier. Practical Cryptography (англ.). — Indianapolis: John Wiley & Sons, 2003. — ISBN 0-471-22357-3.

[provos-6] Provos, Niels^[англ.]; Mazières, David^[англ.]. A Future-Adaptable Password Scheme (неопр.) // Proceedings of the FREENIX Track: 1999 USENIX Annual Technical Conference. — Monterey, CA, USA: USENIX Association, 1999. — 6 June. Архивировано 19 января 2012 года.

[7] U. Manber, "A Simple Scheme to Make Passwords Based on One-Way Functions Much Harder to Crack, " Computers & Security, v.15, n.2, 1996, pp.171-176. (англ.)

[1]

[2]

[3]

[4]

[5]

[6]

[7]