Петля (топология)

Петля в топологическом пространстве X — это непрерывное отображение f единичного отрезка I = [0,1] в X, такое что f(0) = f(1). Другими словами, это путь, начальная точка которого совпадает с конечной.

Две петли a и b на торе.

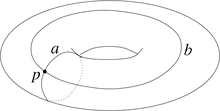
Петлю можно также рассматривать как непрерывное отображение f единичной окружности S¹ в X, поскольку S¹ можно считать факторпространством I при отождествлении 0 с 1.

Пусть X — топологическое пространство, x₀ ∈X. Непрерывное отображение l: S¹ → X, такое что l(1) = x₀, называется круговой петлёй в x₀. Каждой круговой петле в точке x₀ можно сопоставить петлю пространства X в той же точке, взяв композицию l с отображением I →S¹, заданным формулой t →e^2πit. Всякая петля может быть получена из круговой петли таким образом.

Круговые петли называются гомотопными (или эквивалентными), если они {1}-гомотопны (то есть если гомотопия между ними является связанной в точке 1 ∈S¹). Соответствующие классы эквивалентности называются гомотопическими классами петель.

Непустое топологическое пространство называется односвязным, если оно линейно связно и всякая петля в нём гомотопна постоянной петле.

Множество гомотопических классов петель в точке образует группу с операцией композиции путей. Эта группа называется фундаментальной группой пространства X в отмеченной точке x₀.

Множество всех петель в X образует пространство, называемое пространством петель пространства X.

См. также

• Свободная петля
• Группа петель
• Пространство петель
• Алгебра петель
• Фундаментальная группа
• Квазигруппа

Литература

• John Frank Adams. Infinite Loop Spaces. — Princeton University Press, 1978. — Т. 90. — (Annals of mathematics studies). — ISBN 9780691082066.
• О.Я. Виро, О.А. Иванов, Н.Ю. Нецветаев, В.М. Харламов. Элементарная топология. — М.: МЦНМО, 2010. — ISBN 978-5-94057-587-0.