Обсуждение:Теорема Жуковского

Untitled

Уважаемые модераторы энциклопедии «Википедия».

В Вашей энциклопедии я нашел статью, которая, мягко говоря, предоставляет читателям неправдивую информацию.

Предлагаю обсудить на Вашем форуме новое содержание статьи «Теорема Жуковского»:

«ТЕОРЕМА ЖУКОВСКОГО-КУТТА и ПАРАДОКС Д’АЛАМБЕРА-ЭЙЛЕРА – это всего лишь теоретические недоразумения, возникшие на этапе абстрактных рассуждений из-за неправильно выбранных начальных условий.

Теорема Жуковского-Кутта и парадокс Д’Аламбера-Эйлера не имеют никакого отношения к реальным физическим процессам. Более того, содержание теоремы Жуковского-Кутта противоречит закону сохранения энергии.

В соответствии с теоремой Лагранжа (эта теорема является формулировкой закона сохранения энергии для идеальной среды): «Во всех точках баротропно движущейся идеальной среды под действием объемных сил с однозначным потенциалом (т.е. при отсутствии внешних источников энергии) циркуляция вектора скорости по любому замкнутому контуру остается равной нулю».

Из этой теоремы следует: для возникновения отличной от нуля циркуляции вектора скорости (например, вокруг профиля крыла) необходим внешний источник энергии. Но в теореме Жуковского-Кутта ничего не говорится о дополнительных источниках энергии.

Теорема Жуковского-Кутта и парадокс Д’Аламбера-Эйлера по своей бессмысленности и бесполезности стоят на одном уровне с такими «шедеврами», как теория «ТЕПЛОРОДА» в теплофизике и прочими абсурдами».

Этот вариант статьи ещё нуждается в редактировании, но он больше соответствует действительности, чем Ваш вариант статьи.

В более кратком изложении эта статья может содержать только первый, второй и последний абзацы.

Подробности можно найти на сайте: http://dalamberparadox.narod.ru/

— Эта реплика добавлена с IP 80.73.1.89 (о) (Alexandr AUGUST 07:11, 25 ноября 2008 (UTC)?)

Из ВП:ВУ— перенёс Анатолий 09:27, 21 августа 2007 (UTC)

Вам не кажется, что упомянутая теорема Лагранжа как раз более оторвана от действительности (ибо не бывает идеальной бездиссипативной среды)? А теорема Жуковского как раз и пытается учесть существование ненулевой циркуляции в реальной жидкости, пусть и вводя эту характеристику как чужеродную идеальной гидродинамике. infovarius 17:38, 22 августа 2008 (UTC)

ОТВЕТ: Теорема Жуковского-Кутта - это сплошной винегрет из нескольких теоретических моделей, а именно: ОСНОВНАЯ МОДЕЛЬ - безвихревое, безотрывное обтекание твердых тел идеальной средой. В этой модели циркуляция вектора скорости при отсутствии внешних источников энергии всегда равна нулю. И все силы равны нулю в соответствии с парадоксом Д'Аламбера-Эйлера.

Но для объяснения образования циркуляции вокруг профиля крыла в теореме Жуковского-Кутта вводится модель ВЯЗКОЙ СРЕДЫ. А для вязких сред невозможно получить безвихревое безотрывное обтекание.

Вот и получается, что теорема Жуковского-Кутта - это клубок противоречий. Одно утверждение постоянно противоречит со следующими выводами или допущениями.

А теорема Лагранжа является формулировкой фундаментального закона сохранения энергии для идеальной среды. Закон сохранения энергии еще никто не отменял.

Но теорема Жуковского-Кутта, в силу своей бессмысленности, как раз и нарушает ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ.

Если бы эту теорему можно было бы реализовать на практике, то мы бы получили силу (просто так – из ничего), которая может выполнять полезную работу, и при этом не нужно затрачивать никакой энергии. Теорема Жуковского-Кутта – это основа для построения "вечного двигателя".

Конкретный пример: гребной винт корабля или пропеллер. В соответствии с теоремой Жуковского-Кутта сила лобового сопротивления в плоскости вращения винта равна нулю, т.е. для вращения винта с постоянной скоростью не нужно затрачивать никакой энергии. А в результате мы получаем дармовую силу, совпадающую по направлению с осью винта, и эта сила может выполнять полезную работу.

Alexandr AUGUST 07:11, 25 ноября 2008 (UTC)

Полностью согласен с господином Анатолий

Эту теорему не просто можно "реализовать на практике", а она именно, что ИСПОЛЬЗУЕТСЯ на практике и именно для расчета "гребных винтов и пропеллеров".

Теорема Жуковского говорит нам, какую циркуляцию необходимо задать на профиле крыла для того, чтобы структура потоков идеальной и реальной жидкостей вблизи профиля крыла стали подобны. Если угодно, можете полагать, что данная циркуляция возникает за счет трения в пограничном слое.

Тогда, задавая циркуляцию "присоединенных" к лопасти винта вихрей (исходя из требуемого упора винта), мы можем определить требуемые углы атаки цилиндрических сечений лопасти, или, наоборот, задавая геометрию лопасти и удовлетворяя условие непротекания её поверхности, мы получаем интенсивность присоединенных вихрей и по теореме Жуковского определяем силы, действующие на лопасть.

Как показывают расчеты, дармовой силы при этом не возникает - теория позволяет определить не только упор (продольную силу) винта, но и момент, препятствующий его вращению.

См., например:

• В. Ф. Бавин и др. "Гребные винты. Современные методы расчета", Л., Судостроение.
• С. М. Белоцерковский - любую книгу.

Справедливость теоремы Жуковского НЕОДНОКРАТНО подтверждена экспериментами, в том числе, и экспериментами по измерению завихренности вблизи профиля крыла. Для случая идеальной жидкости эксперименты ставились методом ЭГДА

ОСТАВЬТЕ ДЕДУШКУ ЖУКОВСКОГО В ПОКОЕ 8)))

Iatsouk 17:11, 25 ноября 2008 (UTC)

Возражения участника Iatsouk слишком сумбурные и поэтому ничего не доказывают и ничего не опровергают. Давайте попробуем без эмоций спокойно разобраться, давайте попытаемся отделить: отдельно – "котлеты", отдельно – "мух".

Вы утверждаете, что "справедливость теоремы Жуковского-Кутта для случая идеальной жидкости подтверждена моделированием по методу ЭГДА". Этот метод позволяет решать УРАВНЕНИЕ ЛАПЛАСА для идеальной среды по аналогии с электрическими полями. Само уравнение Лапласа является условием безвихревого, безотрывного обтекания идеальной средой твердых тел.

Поэтому построение кинематической картины обтекания идеальной средой твердых тел на основе решения уравнения Лапласа ВСЕГДА приводит к результатам с безвихревым безотрывным обтеканием, а при решении кинематической задачи такие течения всегда приводят к нулевым силовым взаимодействиям (известный парадокс Д'Аламбера-Эйлера). Возникновение отличной от нуля циркуляции вектора скорости (например, вокруг профиля крыла) при решении уравнения Лапласа возможно только при наличии дополнительного источника энергии. Но в теореме Жуковского-Кутта ничего не говорится о дополнительных источниках энергии.

Поэтому решение уравнения Лапласа для идеальной среды без дополнительных источников энергии (например, по методу ЭГДА) не может подтвердить теорему Жуковского-Кутта, а может только ее опровергнуть. При движении твердых тел в идеальной среде получить ОТЛИЧНУЮ ОТ НУЛЯ ПОДЪЕМНУЮ СИЛУ и – НУЛЕВУЮ СИЛУ ЛОБОВОГО СОПРОТИВЛЕНИЯ (т.е. не затрачивая никакой энергии) – невозможно. Поэтому теорема Жуковского-Кутта противоречит закону сохранения энергии.

Для объяснения причин возникновения силы лобового сопротивления и подъемной силы при движении твердых тел в ИДЕАЛЬНОЙ СРЕДЕ хорошей альтернативой модели безвихревого безотрывного обтекания является МОДЕЛЬ ОБТЕКАНИЯ С ОТРЫВОМ СТРУЙ (метод Кирхгофа). Этот метод позволяет рассчитать силу лобового сопротивления при симметричном обтекании идеальной средой твердых тел. Результаты теоретических расчетов вполне адекватно совпадают с экспериментальными измерениями силы лобового сопротивления при движении твердых тел в реальных слабовязких жидкостях и газах. Наличие вязкости в реальных жидкостях и газах приводит к необходимости ввода в эти расчеты поправочных коэффициентов, пропорциональных вязкости среды.

При обтекании идеальной средой несимметричных (относительно первоначального направления вектора скорости) твердых тел в соответствии с моделью Кирхгофа возникает не только сила лобового сопротивления, но и ортогональные силы (подъемная или боковая силы).

Для образования этих сил не нужно выполнять условия Кутты "о передней круглой кромке и острой задней кромке". Подъемная сила возникает в соответствии с моделью Кирхгофа даже, если передняя кромка будет острой, а задняя кромка – закругленной, или обе кромки будут острыми, а также, если обе кромки будут закругленными. И эти результаты хорошо согласуются с экспериментом. В методе Кирхгофа для расчетов ортогональных сил нет надобности вводить "циркуляцию вектора скорости вокруг профиля крыла".

В инженерных экспериментах с конкретными профилями крыльев самолетов или лопастей пропеллеров методом продувки в аэродинамических трубах измеряют зависимость коэффициента Сх (этот коэффициент пропорционален силе лобового сопротивления) от угла атаки и аналогичной зависимости коэффициента Cy (этот коэффициент пропорционален ортогональной подъемной силе). Построив график зависимости отношения этих коэффициентов Сy/Сx от углов атаки, можно определить оптимальный угол атаки или критический угол атаки для конкретного профиля.

Обратите внимание: во всех инженерных экспериментах и теоретических расчетах не нужна циркуляция вектора скорости вокруг профиля крыла – потому что ее не существует в природе. Метод Кирхгофа с отрывом струй хорошо объясняет возникновение и силы лобового сопротивления и подъемной силы без "пресловутой циркуляции".

Обратите также внимание на то, что теорема Жуковского-Кутта не может объяснить: почему плавают рыбы в воде, махая хвостом перпендикулярно направлению движения? Возникновению "пресловутой циркуляции" вокруг хвоста рыб мешает корпус рыбы. А без такой циркуляции в соответствии с теоремой Жуковского-Кутта рыбы не могут плавать.

А метод Кирхгофа с отрывом струй хорошо объясняет возникновение сил, необходимых для плавания рыб.

Общий вывод – теорема Жуковского-Кутта, объясняющая возникновение подъемной силы при нулевой силе лобового сопротивления наличием циркуляции вектора скорости вокруг профиля крыла с закругленной передней кромкой и острой задней кромкой – является всего лишь теоретическим недоразумением. Ни в теоретических расчетах, ни в экспериментах нельзя подтвердить наличие этой циркуляции, потому что возникновение такой циркуляции без дополнительных источников энергии – это прямое нарушение закона сохранения энергии.

Птицы миллионы лет летают и рыбы плавают не благодаря теореме Жуковского-Кутта, а вопреки этой теореме, и это лучшее доказательство ее бессмыленности.

Alexandr AUGUST 08:01, 8 декабря 2008 (UTC)

• "в теореме Жуковского-Кутта ничего не говорится о дополнительных источниках энергии".

Прямо и непосредственно в теореме об этом, действительно не говорится. Однако, об этом говорят (и пишут) гидромеханики, когда обсуждают эту теорему. А именно: энергия, необходимая для образования вихрей, извлекается из набегающего потока силами трения, действующими в пограничном слое.

В методе ЭГДА, действительно, приходится подводить дополнительную энергию, для создания на исследуемом профиле необходимой циркуляции, но это лишь потому что мы не умеем создавать силы трения в электромагнитном поле.

• "Обратите внимание: во всех инженерных экспериментах и теоретических расчетах не нужна циркуляция вектора скорости вокруг профиля крыла – потому что ее не существует в природе." , "Возникновению "пресловутой циркуляции" вокруг хвоста рыб мешает корпус рыбы."

Начну с природы: Циркуляция скорости таки существует, ибо циркуляция это всего/навсего интеграл от скорости по некоторому криволинейному контуру. И, как показывают результаты измерений полей скоростей вблизи тел, этот интеграл, вычисленный по экспериментальным данным очень хорошо соответствует величине, предсказанной Н. Е. Жуковским.

Продолжу теоретическими расчетами: вся современная теория проектирования судовых гребных винтов основана на теории Жуковского. Упоминавшаяся уже мной книга В. Ф. Бавина с соавторами написана почти 30 лет назад и уже тогда она была обобщением существующего реального опыта проектирования. За минувшие годы, с использованием этой теории, были спроектированы, изготовлены и установлены на судах десятки тысяч гребных винтов - и каждое судно, после постройки, побывало на приемо-сдаточных ходовых испытаниях - и, полагаю, подавляющее большинство из этих судов смогло развить контрактную скорость, предсказанную (в том числе) и с помощью теории Жуковского.

• О законе сохранения энергии.

В теории вихрей доказываются и используются теоремы Томсона и Гельмгольца, из которых следует, что вихри не могут возникнуть либо исчезнуть в идеальной жидкости. Собственно, эти теоремы можно рассматривать в качестве закона сохранения энергии для случая движения вихрей в идеальной жидкости.

В реальной жидкости, как нам известно, вихри возникают. Например, вот здесь http://en.wiki.x.io/wiki/Ship_model_basin можно посмотреть на классическую фотографию, полученную в кавитационной трубе "Cavitating propeller in a water tunnel experiment at the David Taylor Model Basin" на которой отчетливо видны концевые вихри, образующиеся на лопастях гребного винта.

Причины возникновения вихрей в реальной среде понятны: действие сил трения а также (в случае атмосферы) температурная и "влажностная" неоднородность.

Так откуда берутся вихри в идеальной жидкости? Их помещаем туда мы, гидромеханики, чтобы учесть те явления которые в идеальной жидкости реализоваться иначе не могут. Сколько нужно поместить вихрей - об этом говорит теорема Жуковского.

• "Общий вывод"

Теория Жуковского является широко известной, общепризнанной и подтвержденной результатами эксперимента. Этого довода УЖЕ достаточно, для того, чтобы она была отражена на страницах данной энциклопедии. Вы, как и любой другой участник, имеете несомненное право в конце странички, посвященной теории Жуковского поместить свои возражения против неё, естественно, со ссылкой на "авторитетные источники". От себя замечу, что "умение рыб плавать" и некий сайт на "народ.ру" не являются авторитетными источниками.

• Кстати!

Знаете ли Вы, что всё то, что именуется современным "математическим анализом" основано на теории множеств Кантора и так называемой "аксиоме непрерывности". Теория множеств Кантора противоречит сама себе - относительно "множества всех множеств" можно доказать взаимно исключающие утверждения.

А эта "аксимома непрерывности": Вы только представьте (!) если проткнуть вещественную ось иголкой (!!) то, как утверждается математиками, на конце иголки обязательно обнаружится число (!!!).

И вот на таких, с позволения сказать, "основаниях" математики парят мозги жителям всей планеты. Может быть, Вам стоит не растрачивать себя по мелочам, а заняться, проблемой, имеющей воистину всепланетное значение?

8))
Iatsouk 09:48, 8 декабря 2008 (UTC)

Уважаемый участник Iatsouk . Вашу бы настойчивость в отстаивании и защите бессмысленной, бесполезной и нереализуемой теории Жуковского-Кутта направить бы в полезное русло – можно было бы горы свернуть.

Но не все так уж и безнадежно. Уже сделан первый шаг! Мы с Вами пришли к консенсусу о том, что «Решение уравнения Лапласа для идеальной среды (например, по методу ЭГДА) без дополнительных источников энергии не может подтвердить теорему Жуковского-Кутта, а может только ее опровергнуть».

Вот так, двигаясь шаг за шагом (step by step), можно прийти к консенсусу и по другим вопросам.

Попробую ответить на Ваш вопрос: «Так откуда берутся вихри в идеальной жидкости? Их помещаем туда мы, гидромеханики, чтобы учесть те явления, которые в идеальной жидкости реализоваться иначе не могут. Сколько нужно поместить вихрей – об этом говорит теорема Жуковского».

Это большое преувеличение. Объяснять физические явления только волюнтаристскими действиями «несознательных гидромехаников» – ЭТО УЖЕ ПЕРЕБО-О-ОР. Появление вихрей при обтекании твердых тел идеальной средой нужно объяснять только физическими процессами.

При построении кинематической картины течения идеальной среды вокруг твердых тел на основе решения уравнения Лапласа получается безвихревое, безотрывное обтекание. Но в большинстве случаев такая картина течения в соответствии с уравнением Бернулли приводит к решениям с отрицательными давлениями в идеальной среде (и даже к бесконечно большим отрицательным давлениям при обтекании острых кромок). (см., например, 1. Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидродинамика. Ч.1./ Под ред. И.А. Кибеля. Издание шестое.- М.: Гос. из-во физ.-мат. лит., 1963. 2. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика : Учебное пособие. В 10 т. Т.6. Гидродинамика.- 4-е изд. стер.- М.: Наука. Гл. ред. физ.-мат. лит., 1988.- 736с.)

Учитывая физическую бессмысленность понятия «отрицательное давление», необходимо при расчетах кинематической картины течения обязательно вводить ограничение: ДАВЛЕНИЕ В ИДЕАЛЬНОЙ СРЕДЕ (а также в реальных жидкостях и газах) ДОЛЖНО БЫТЬ ВСЕГДА БОЛЬШЕ НУЛЯ.

С учетом этого ограничения при расчетах кинематической картины обтекания твердых тел идеальной средой МЕТОДОМ ПОСЛЕДОВАТЕЛЬНЫХ ИТЕРАЦИЙ приходят к решениям с отрывом струй (метод Кирхгофа). Отходящие от твердого тела струи или поверхности тангенциального разрыва с математической точки зрения являются ВИХРЯМИ (т.е. ротор вектора скорости на поверхности тангенциального разрыва отличен от нуля). Позади твердого тела между поверхностями тангенциального разрыва образуется "застойная зона". Для идеальной среды эти поверхности тангенциального разрыва уходят в бесконечность, а для реальных жидкостей и газов эти поверхности распадаются на отдельные вихри (за счет вязкого взаимодействия между слоями), эти вихри заполняют застойную зону и, в дальнейшем, эти вихри диссипируют на конечном расстоянии позади твердого тела.

Аналогичные рассуждения приводят к модели обтекания твердого тела идеальной средой с вихревыми дорожками Кармана.

Образование этих вихрей позади твердого тела объясняет механизм появления силы лобового сопротивления при симметричном обтекании идеальной средой твердых тел. При обтекании несимметричных твердых тел результирующую силу взаимодействия твердого тела с идеальной средой можно разложить на составляющие: силу лобового сопротивления и ортогональные силы – подъемную и боковую силы.

И НИКАКОГО ВОЛЮНТАРИЗМА «несознательных гидромехаников» придумывать не нужно. Образование вихрей позади твердого тела при обтекании его идеальной средой (а тем более при обтекании реальными жидкостями и газами) – это ОБЪЕКТИВНЫЙ физический процесс.

Метод Кирхгофа (т.е. обтекание твердых тел идеальной средой с вихреобразованием) объясняет появление подъемной силы для профилей с острой передней кромкой, с острыми обеими кромками и закругленными обеими кромками. Метод Кирхгофа позволяет объяснить: почему плавают рыбы? (В соответствии с теоремой Жуковского-Кутта рыбы не могут двигаться). И никакой циркуляции вокруг обтекаемого профиля выдумывать (т.е. высасывать из пальца) не нужно.

Еще одно Ваше весьма спорное утверждение: «В теории вихрей доказываются и используются теоремы Томсона и Гельмгольца, из которых следует, что ВИХРИ НЕ МОГУТ ВОЗНИКНУТЬ либо исчезнуть в идеальной жидкости».

Ваши заблуждения основаны на том, что Вы не дочитала до конца эту теорему Томсона (Кельвина), в которой доказывается «неизменность циркуляции скорости (или неизменность вихря скорости) во всех точках баротропно движущейся идеальной среды под действием объемных сил с однозначным потенциалом».

По условию этой теоремы циркуляция остается неизменной при отсутствии в потоке дополнительных источников энергии, т.е. движение осуществляется только по инерции (при движении по горизонтали объемная сила гравитации не участвует в расчетах).

При внесении в поток идеальной среды дополнительных источников энергии циркуляция вектора скорости МОЖЕТ ВОЗНИКНУТЬ (или в общем случае измениться в сторону увеличения или уменьшения).

Попробую опровергнуть еще одно Ваше сомнительное утверждение: «Теория Жуковского является широко известной, общепризнанной и подтвержденной результатами эксперимента». В качестве аргумента приведена ссылка на фотографию гребного винта в кавитационном туннеле на сайте http://en.wiki.x.io/wiki/Ship_model_basin.

Эта фотография не подтверждает теорему Жуковского-Кутта, а доказывает ее бессмысленность. Позади гребного винта (на фотографии это слева от винта) мы видим вихревые струи, которые отходят от задней кромки лопасти винта в виде поверхностей тангенциального разрыва. Если увеличить масштаб фотографии в 4 и более раз, то можно рассмотреть еще и струи, которые срываются с передней кромки лопасти винта.

Единственное, чего нельзя увидеть на этой фотографии, так это БЕЗОТРЫВНОГО обтекания вокруг профиля лопасти винта и циркуляцию вокруг этой лопасти в соответствии с теоремой Жуковского-Кутта.

Ваша проблема заключается в том, что Вы путаете те вихри (поверхности тангенциального разрыва), которые срываются с задней кромки лопасти винта в соответствии с теорией Кирхгофа, с той циркуляцией, которая должна якобы возникнуть ВОКРУГ лопасти винта в соответствии с теорией Жуковского-Кутта.

Показанные на фотографии вихри (слева от гребного винта) не имеют никакого отношения ни к Жуковскому, ни к Кутту. В соответствии с классической интерпретацией теоремы Жуковского-Кутта (см., например, сайт: http://www.effects.ru/science/91/index.htm) поток идеальной среды безотрывно обтекает профиль и не образует вихрей позади профиля.

Поэтому, показанные на фотографии отрывы струй, как с передней, так и с задней кромки лопасти винта подтверждают метод Кирхгофа и опровергают безотрывное обтекание с образованием «циркуляции» вокруг профиля лопасти винта в соответствии с теоремой Жуковского-Кутта.

И еще одна небольшая историческая справка. Метод Кирхгофа был опубликован значительно раньше, чем теорема Жуковского-Кутта. Поэтому Жуковский и Кутт знали (или могли знать) о методе Кирхгофа. Но решили «пойти другим путем». И этот путь оказался тупиковым. С теоретической точки зрения теорема Жуковского-Кутта является абсолютно бессмысленной, потому что противоречит закону сохранения энергии, а с практической точки зрения она является бесполезной, потому что невозможно реализовать безвихревое безотрывное обтекание твердых тел реальными вязкими жидкостями и газами. Фотография гребного винта в кавитационном туннеле еще раз это подтверждает.

Alexandr AUGUST 09:02, 15 декабря 2008 (UTC)

• "Показанные на фотографии вихри (слева от гребного винта) не имеют никакого отношения ни к Жуковскому, ни к Кутту." "... с практической точки зрения она является бесполезной, потому что невозможно реализовать безвихревое безотрывное обтекание твердых тел реальными вязкими жидкостями и газами."

По Жуковскому ("схема несущей линии") крыло (лопасть) заменяется "присоединенным вихрём", который на кромках крыла переходит в "свободные" вихри, сносимые потоком. На присоединенном вихре возникает подъемная сила, на свободных - нет. По Жуковскому (схема "несущей поверхности") крыло заменяется системой (слоем) "присоединенных" вихрей, интенсивность которых изменяется как по размаху (радиусу винта) так и по хорде. Интенсивность свободного вихревого слоя (по-прежнему сносимого потоком) также как и в предыдущем случае отвечает теоремам Гельмгольца и Томсона. Таким образом, никто и не пытается "реализовать безвихревое безотрывное обтекание твердых тел реальными вязкими жидкостями и газами". Когда у Жуковского говорится о "безотрывном обтекании" имеется в виду отсутствие отрыва на входящей и выходящей кромках, которое наблюдается при относительно малых углах атаки. От вихреобразования на торцах крыла (кромке лопасти и ступице винта) Жуковский НЕ ОТКАЗЫВАЛСЯ - см., напр., схему "бесконечнолопастного винта" (винта с бесконечно большим числом лопастей), предложенную Жуковским.

Упомянутая фотография получена в кавитационной трубе (при пониженном гидростатическом давлении) при стробоскопическом освещении. Пузыри, замеченные Вами над лопастью - каверны на засасывающей стороне профиля, а отчетливо различимые свободные концевые вихри, также заполненные кавернами, являются убедительнейшим доказательством справедливости вихревой теории винта, неотъемлемой частью которой является обсуждаемая теорема.

• "Попробую опровергнуть еще одно Ваше сомнительное утверждение: «Теория Жуковского является широко известной, общепризнанной и подтвержденной результатами эксперимента».

"В качестве аргумента приведена ссылка на фотографию..." Относительно фотографии см. выше. А вот в качестве аргументов, на самом деле, были приведены ссылки на: а) научно-техническую литературу; б) результаты НАТУРНЫХ испытаний судов, оборудованных гребными винтами

В настоящее время проектировочный расчет гребных винтов (см., напр., http://www.smtu.ru/smtu/rus/ktk/state/achkinad.htm) выполняется ИСКЛЮЧИТЕЛЬНО с применением вихревой теории. Поверочный расчет гребных винтов выполняется либо с использованием вихревой теории либо с использованием RANS.

В общем, опровержение у Вас не получилось.

• "Но не все так уж и безнадежно."

Учитывая, что: а) Похоже, все именно безнадежно и дальнейшая дискуссия с Вами бесполезна. Вы упорно игнорируете ссылки на общепризнанную литературу, а в тех случаях, когда вспоминаете о её существовании попросту занимаетесь подтасовками - напр., у КочКибРозе теории Жуковского-Кутта и Кирхгофа обсуждаются как равноправные;

б) Данная страница предназначена не для "обсуждения предмета статьи", а для "обсуждения статьи" (см. Правила в верхней части страницы);

в) Моя личная загрузка не позволяет мне тратить время (опытовый бассейн, в котором я работаю приступает к испытаниям нового проекта судна, кстати, винт будем опять проектировать "по-Жуковскому"),

я не намерен продолжать данную дискуссию. 

В качестве последнего шага, если, разумеется, это Вас заинтересует я готов выслать Вам: а) маткад-программу поверочного расчета гребного винта "по Жуковскому". б) статью с описанием программы и результатов расчета. в) ссылки на данные по геометрии и гидродинамическим характеристикам широко распространенных винтов.

• В завершение я лишь ПОВТОРНО обращу Ваше внимание на формальные принципы отбора материалов для Википедии:

а) информация должна быть взята из "авторитетных источников" - таковыми являются, например, упомянутый Вами двухтомник КочКибРозе, а также приведенной мной ссылки; б) информация должна отвечать "критерию значимости" - как я уже указывал ранее, вихревая теория чрезвычайно широко используется при проектировании гребных винтов (снова см. упомянутые ссылки).

Поскольку оба условия ВЫПОЛНЕНЫ данная статья заслуженно занимает свое место в Википедии. Iatsouk 22:31, 15 декабря 2008 (UTC)

---

___

Уважаемый участник Iatsouk .

Ваши аргументы о том, что: "В настоящее время проектировочный расчет гребных винтов выполняется ИСКЛЮЧИТЕЛЬНО с применением вихревой теории" а также ссылка на фотографию, которая "является убедительнейшим доказательством справедливости вихревой теории винта" – подтверждает справедливость модели Кирхгофа об обтекании твердых тел идеальной средой с отрывом струй. Эта же модель обтекания твердых тел с вихреобразованием вполне адекватно описывает и реальные процессы с вязкими жидкостями и газами. В этом вопросе мы с Вами ПРИШЛИ К КОНСЕНСУСУ.

Однако совсем непонятно, какое отношение к этим вихрям имеет модель Жуковского-Кутта безотрывного безвихревого обтекания профиля крыла с образованием подъемной силы за счет "высосанной из пальца" циркуляции вокруг профиля крыла? Появление такой циркуляции без дополнительных источников энергии противоречит закону сохранения энергии.

Я Вам искренне верю, что "маткад-программа поверочного расчета гребного винта" основана на вихревой модели. Но причем здесь теорема Жуковского-Кутта с безотрывным безвихревым обтеканием?

В Ваших аргументах произошла подтасовка фактов – несуществующую циркуляцию Вы заменяете термином "присоединенный вихрь", потому что во всех экспериментах Вы показываете студентам отходящие от твердого тела поверхности тангенциального разрыва, которые распадаются на отдельные вихри за счет вязкого взаимодействия между слоями жидкости. Поэтому и доказательства у Вас на уровне Остапа Бендера: "И пусть первый бросит в меня камень тот, кто скажет, что это не вихри!!?".

Да, вихри действительно есть за счет отрыва струй от кромок твердого тела в соответствии с моделью Кирхгофа. Но эти вихри не имеют никакого отношения ни к Жуковскому, ни к Кутту. И называть эти поверхности тангенциального разрыва ПОЗАДИ кромок твердого тела "присоединенными вихрями ВОКРУГ профиля твердого тела" – у Вас нет никаких оснований.

Сама математическая формула теоремы Жуковского-Кутта (см. страницу "теорема Жуковского" в ВИКИПЕДИИ) вполне адекватно описывает эффект Магнуса с образованием подъемной силы за счет циркуляции вектора скорости вокруг вращающегося цилиндра. Но для образования этой циркуляции в опытах с вращающимся цилиндром (или в опытах, показанных Жуковским Н.Е. с вращающейся полоской бумаги) необходимо затрачивать энергию. Поэтому никаких противоречий с законом сохранения энергии в эффекте Магнуса нет.

Позволю себе небольшое общетеоретическое отступление:

Причины путаницы и подтасовок в доказательствах теоретической бессмыслицы, которая противоречит основополагающему закону сохранения энергии, – в отсутствии общесистемных знаний и, как следствие, в отсутствии системного мышления.

Существующая сегодня система фрагментарного (отрывочного, модульного, бессистемного) образования приводит к фрагментарным (отрывочным) знаниям и, как следствие, к фрагментарному мышлению. Основа фрагментарного образования – это преклонение перед "известными авторитетами". Тоталитарная (т.е. не допускающая инакомыслия) система образования не может и, в принципе, не ставит своей целью воспитания системного мышления.

Именно системное мышление не позволяет принять модель Жуковского-Кутта безотрывного обтекания профиля крыла, которая противоречит закону сохранения энергии, а также приводит к многочисленным противоречиям и бессмысленным результатам, а именно: эта модель не может объяснить, почему возникает подъемная сила при обтекании твердых тел с передней острой кромкой, почему теоретические расчеты для обтекания твердых тел с передней отстрой кромкой приводят к бессмысленным результатам с отрицательными давлениями, почему двигаются рыбы, у которых образованию циркуляции вокруг хвоста мешает корпус, и много других противоречий.

"Высшим пилотажем" или "верхом совершенства" при фрагментарном мышлении является умение "закрывать глаза" или "не видеть в упор" эти и многие другие системные противоречия, про которые стыдливо умалчивают "известные авторитеты".

Бессмысленной модели Жуковского-Кутта разумной альтернативой является вихревая модель Кирхгофа обтекания твердых тел идеальной или реальной средой с отрывом струй. Эта модель не противоречит закону сохранения энергии и вполне адекватно объясняет все перечисленные (и многие другие) процессы в природе.

Каждый должен выбрать для себя – нужны ли ему общесистемные знания, которые не противоречат базовым физическим законам (тогда внимательно прочитайте мои комментарии с самого начала на этой странице), или ему достаточно знать то, что ему пытаются "пропихнуть" как точку зрения "известных авторитетов".

Alexandr AUGUST 10:11, 24 декабря 2008 (UTC)

Хоть и пообещал не писать, но отвечу.

Схемы обтекания крыла бесконечного размаха по Жуковскому-Чаплыгину

• 1. У Вас в корне неверное (по Вашей классификации - тоталитарно/фрагментарное) представление о постулате ЖЧ. Как я Вам уже указывал термин "безотрывное обтекание";;;;;;;;;;;;;;;; говорит лишь об отсутствии отрывов с передней и задней кромок крыла БЕСКОНЕЧНОГО размаха (см. рис.), но допускает появление свободных вихрей, сходящих с крыла конечного размаха. Постулат это не теорема, это всего-лишь утверждение, обобщающее результаты наблюдений и измерений, такое же как, например, аксиомы Евклидовой геометрии. (Вам не нравится "фрагментарный" Евклид - пожалуйста пользуйтесь "системной" теорией Лобачевского.) Постулат ЖЧ относится лишь к сравнительно малым углам атаки и стационарному обтеканию.

• 2. Циркуляция, как я опять-таки уже писал, это всего лишь криволинейный интеграл от скорости по замкнутому контуру. Он (интеграл) существует ВСЕГДА, в частном случае он может быть равен нулю. Если промерить поле скоростей вокруг крыла и вычислить этот интеграл, то окажется, что он НЕ РАВЕН нулю и, более того, весьма близок к величине, определяемой по Н. Е. Жуковскому.

• 3. На Ваш вопрос "какое отношение имеет постулат ЖЧ к вихревой теории крыла?" имею сообщить следующее: в вихревой теории крыла постулат ЖЧ используется в качестве граничного условия (совместно с условием непротекания), позволяющего однозначно определить ту самую циркуляцию присоединенных вихрей в которую Вы не верите. После того, как циркуляция определена, теорема Жуковского позволяет найти силу, действующую на крыло. И никакого Кирхгофа.

Таким образом, постулат ЖЧ и теорема Жуковского являются неотъемлемой частью вихревой теории крыла (гребного винта). Перефразируя Маяковского: "Вихревая теория крыла и постулат ЖЧ - близнецы-братья. Кто более матери-истории ценен ?... "

• ЗЫ:

Огромная просьба: если у Вас осталось желание обзавестись "системным" представлением о вихревой теории крыла, задавайте Ваши вопросы на моей личной странице участника. Здесь не подходящее для этого место, если нас поймают администраторы - могут отключить доступ, а я бы этого не хотел.

Iatsouk 21:25, 24 декабря 2008 (UTC)

_____________

Уважаемый участник Iatsouk.

Ваши последние возражения позволяют сделать вывод о том, что Вы окончательно запутались в попытках оправдать теоретически бессмысленную и поэтому практически нереализуемую модель Жуковского-Чаплыгина-Кутта. Ваши высказывания противоречат одно другому.

Приведу примеры: Вы утверждаете, что «в постулате ЖЧ … термин "безотрывное обтекание" говорит лишь об отсутствии отрывов с передней и задней кромок крыла БЕСКОНЕЧНОГО размаха (ссылка на верхний рисунок в Ваших возражениях), но допускает появление свободных вихрей, сходящих с крыла конечного размаха», т.е. Вы совместно с Ж-Ч допускаете только вихри на торце крыла конечного размаха и не допускаете вихри (или поверхности тангенциального разрыва) с передней и задней кромок профиля крыла. Вы также утверждаете, что «постулат ЖЧ относится лишь к сравнительно малым углам атаки».

А после этого Вы заявляете, что «постулат ЖЧ и теорема Жуковского являются неотъемлемой частью вихревой теории крыла (гребного винта)». Но при этом ссылаетесь на свой средний рисунок с отрывом струй от передней и задней кромок профиля крыла и разделением этих струй на отдельные вихри.

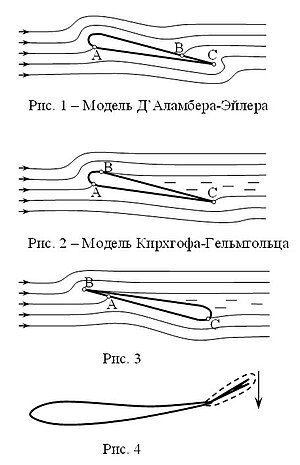
Я попытаюсь объяснить причины Ваших противоречий. Для этого я преобразовал Ваш нижний рисунок к классическому виду (см. рис. 1). Такая кинематическая картина течения является результатом решения уравнения Лапласа (можно даже методом ЭГДА).

На рис. 1 средняя линия тока в точке А разделяется на две линии тока, примыкающие к профилю крыла, и от точки В, объединяясь в одну линию, уходит в бесконечность. Скорость в точках А и В равна нулю, поэтому в соответствии с уравнением Бернулли в этих точках получается максимальное давление по профилю крыла.

В точке С за острой кромкой присутствует бесконечно большое отрицательное давление (в соответствии с уравнением Эйлера), потому что изгиб линии тока на острой кромке свидетельствует о бесконечно большом нормальном ускорении на острой кромке. За передней закругленной кромкой крыла также может возникнуть отрицательное давление в соответствии с уравнением Бернулли при увеличении скорости потока или при уменьшения радиуса закругления.

Учитывая физическую бессмысленность понятия «отрицательное давление», а тем более «бесконечно большое отрицательное давление», Гельмгольц в середине 19-го века предложил вихревую модель обтекания идеальной средой твердых тел с отрывом струй (см. рис. 2 и 3). Эта модель была доведена Кирхгофом до конкретных математических формул. В точках В и С от твердого тела отходят поверхности тангенциального разрыва. Между этими поверхностями образуется застойная зона (на рис. 2 и 3 застойная зона показана пунктирными линиями). В реальных вязких жидкостях и газах эти поверхности тангенциального разрыва распадаются на отдельные вихри и заполняют застойную зону, как на Вашем среднем рисунке.

Циркуляции вектора скорости вокруг профилей крыльев на Вашем среднем рисунке и на моих рисунках 2 и 3 равны нулю (и никаких «присоединенных вихрей» там нет). Поэтому ни о какой подъемной силе в соответствии с теоремой Жуковского-Кутта говорить не приходится. Тем не менее, и сила лобового сопротивления – Fx и подъемная сила – Fy в этих экспериментах отличны от нуля и хорошо согласуются с расчетами в соответствии с вихревой моделью Кирхгофа. Причем подъемная сила возникает даже при повороте крыла острой кромкой вперед (см. рис. 3) или при обтекании плоской пластины (с двумя острыми кромками), установленной под углом к вектору скорости потока. Ни о каком безотрывном обтекании, а тем более ни о какой отличной от нуля циркуляции вектора скорости вокруг профиля крыла говорить не приходится.

Для того, чтобы получить отличную от нуля циркуляцию вектора скорости вокруг профиля крыла необходимо в модели Кирхгофа-Гельмгольца (см. рис. 2) передвинуть точку отрыва струи (точку В) к задней острой кромке крыла (к точке С). Т.е. мы получаем кинематическую картину течения аналогичную верхнему рисунку на Ваших картинках.

Но для этого необходим дополнительный источник энергии (который не показан на Вашем верхнем рисунке). Постулат Жуковского-Чаплыгина, изображенный на Вашем верхнем рисунке, противоречит закону сохранения энергии.

Само слово «Постулат» в соответствии с толковым словарем Ожегова означает: «исходное положение, допущение, принимаемое без доказательств, аксиома». Но принимать без доказательств исходные положения, противоречащие базовому закону сохранения энергии – это ПЕ-РЕ-БОР.

Чего только ни придумывали за последние сто лет для того, чтобы объяснить безотрывное обтекание профиля крыла. Например: «сначала необходимо рассматривать это течение как невязкое с бесконечными скоростями на тонких кромках твердых пластин (см. рис. 1 или Ваш нижний рисунок) и затем преобразовать его в реальное течение с помощью ВНЕЗАПНОГО ДОБАВЛЕНИЯ ВЯЗКОСТИ, … а результирующее течение (на Вашем верхнем рисунке) можно опять рассматривать как невязкое – роль вязкости заключается в становлении его» (Кюхеман Д. Аэродинамическое проектирование самолетов. Пер. с англ./ Пер. Н.А. Благовещенский, Г.И. Майкапар. – М.: Машиностроение, 1983). Пытались также притулить к этой модели «эффект Коанды» и многое другое.

Но получить кинематическую картину течения с безотрывным обтеканием, изображенную на Вашем верхнем рисунке можно только при о-о-очень маленькой скорости потока V. В соответствии с формулой Кирхгофа: сила лобового сопротивления: Fx = Cx * ρ * V^2 и подъемная сила Fy = Cy * ρ * V^2 , т.е. пропорциональны квадрату скорости и при о-о-очень маленькой скорости стремятся к нулю. Вспомните график параболы. При нулевом значении аргумента квадратичная функция имеет нулевую производную, т.е. малые приращения скорости приводят к практически нулевым результатам.

Вы говорили, что: «Постулат ЖЧ относится лишь к сравнительно малым углам атаки». И только при выполнении условия Кутта – закругленная передняя кромка и острая задняя кромка. Вы сами поставили себя в эти ОЧЕНЬ УЗКИЕ РАМКИ, которые значительно раздвигаются в инженерных экспериментах с обтеканием ЛЮБЫХ твердых тел, несимметричных относительно вектора скорости обтекаемого потока. Притулить к этим экспериментам «отличную от нуля циркуляцию вектора скорости вокруг профиля твердого тела» в большинстве случаев не удается (см. например рис. 3).

Я многократно приводил пример о невозможности объяснить в рамках постулата Ж-Ч-К возникновение сил, необходимых для плавания рыб при поперечных движениях хвостом (см. рис. 4). Никакой «отличной от нуля циркуляции вектора скорости» (на рис. 4 эта циркуляция обозначена пунктиром) вокруг хвоста рыбы нет, потому что нельзя замкнуть контур через туловище рыбы. А модель Кирхгофа-Гельмгольца с отрывом струй замечательно объясняет механизм образования сил в направлении движения рыб (на рис. 4 рыба движется влево).

Вы упорно отказываетесь признавать не только противоречие модели Жуковского-Кутта закону сохранения энергии, но и не хотите признавать, что эта модель не сможет объяснить большинство результатов в инженерной практике (некоторые эксперименты я уже описал выше). Ваша стратегия основана на известном выражении: «Если я не вижу проблемы, значит – ее не существует».

В подтверждение сказанному приведу две цитаты (из вступления Седова Л.И. к книге: Биркгоф Г. Гидродинамика. Методы. Факты. Подобие./ Пер. с англ. И.Б.Погребского. Под ред. М.И.Гуревича, В.А.Смирнова. - М.: Из-во иностранной литературы, 1963.): «Ученые-теоретики стремятся оставить в тени те неудобные факты, которые не укладываются послушно в рамки простой логической теории. В то же время инженеры, постоянно соприкасающиеся c действительностью под открытым небом и в лаборатории, обычно слишком перегружены частными техническими задачами, и им практически недоступно участие в академических дискуссиях. Ведь легче воздать на словах должное общепризнанным теориям, а при решении конструкторских проблем полагаться на опыт и интуицию», и еще одна цитата: «Гидродинамики разделяются на инженеров-гидравликов, которые наблюдают то, что нельзя объяснить, и математиков, которые объясняют то, что нельзя наблюдать»

Ваше высказывание: «Вихревая теория крыла и постулат ЖЧ - близнецы-братья» противоречит хронологии. Правильно было бы сказать, что это – дедушка и внук. Вихревая теория обтекания твердых тел с отрывом струй (модель Кирхгофа-Гельмгольца) была предложена значительно раньше модели безотрывного безвихревого обтекания Жуковского-Чаплыгина-Кутта.

И еще одно Ваше предложение о переносе нашего обсуждения на «личную страницу участника» я считаю нецелесообразным. Устраивать банальный «междусобойчик» по вопросу о противоречии статей в ВИКИПЕДИИ базовым физическим законам – это несовместимо с определением «ЭНЦИКЛОПЕДИЯ». Хотелось бы узнать точку зрения Ваших коллег (вернее – наших коллег) по обсуждаемым проблемам.

За этими всеми хлопотами как-то забылось, что сейчас проходят новогодние и рождественские праздники. Я поздравляю Вас с этими радостными праздниками и надеюсь, что в наступившем году мы придем с Вами к консенсусу по обсуждаемым вопросам.

С уважением Alexandr AUGUST 09:46, 9 января 2009 (UTC)

Я также поздравляю Вас с прошедшими праздниками! Однако, на консенсус по поводу обсуждаемого постулата я, честно говоря, не слишком рассчитываю, ибо стараюсь не ставить перед собой заведомо недостижимых целей 8))).

• "За этими всеми хлопотами как-то забылось, что сейчас проходят новогодние и рождественские праздники."

у нас Заказчики сорвали сроки предоставления исходных данных и теперь мы вкалываем ежедневно. Это письмо я пишу вместо того, чтобы обрабатывать данные 8))

• "Вы совместно с Ж-Ч допускаете только вихри на торце крыла конечного размаха и не допускаете вихри (или поверхности тангенциального разрыва) с передней и задней кромок профиля крыла."

Нет, не так. Отрицается возможность появления вихрей, ось которых направлена ВДОЛЬ кромки (при малых углах атаки), вихри, ось которых направлена под прямым углом к кромке - ОБЯЗАНЫ ПРИСУТСТВОВАТЬ в случае крыла конечного размаха и от них никто не отказывается. Существует и описывается в литературе УПРОЩЕННАЯ схема, в которой действительно присутствует лишь концевой вихрь - но это именно предельно упрощенная схема, что каждый раз указывается при её представлении.

• "Вы также утверждаете, что «постулат ЖЧ относится лишь к сравнительно малым углам атаки»." "Вы сами поставили себя в эти ОЧЕНЬ УЗКИЕ РАМКИ"

Под малыми углами атаки здесь понимаются углы до 10...15 градусов (в зависимости от удлинения крыла) - угол, при котором постулат становится не применим, легко определяется по кривой зависимости коэфиициента подъемной силы от угла атаки - как только эта зависимость стала нелинейной - так, всё, дальше по этой теории, действительно никак. Не скажу про самолетные крылья, а вот про лопасти винта знаю точно - углы атаки сечений лопасти составляют 1...3 градуса - т.е. заведомо в области применимости постулата Ж-Ч. "Очень узкие рамки" оказываются весьма широки.

• "Учитывая физическую бессмысленность понятия «отрицательное давление»"

Вы имеете в виду ПОЛНОЕ давление или лишь его динамическую (образовавшуюся за счет движения среды) составляющую? Полное давление = статическое + динамическое, и даже, если динамическое отрицательно сумма будет больше нуля. Вблизи лопастей тяжелонагруженных судовых гребных винтов часто наблюдается явление кавитации - образование каверн, заполненных парами жидкости.

• "Само слово «Постулат» в соответствии с толковым словарем Ожегова означает: «исходное положение, допущение, принимаемое без доказательств, аксиома»."

Полностью согласен с г-ном Ожеговым. Именно об этом я писал выше, когда сравнивал постулат ЖЧ с аксиомами Евклида. И, как я уже писал выше, этот постулат появился не на пустом месте - он обобщает опыт экспериментальных исследований течений жидкости и газа. Вот в этой трубе для того, чтобы увидеть постулат Жуковского-Чаплыгина своими глазами достаточно поставить в рабочую часть крылышко,нажать кнопочку на пульте и взять в руки указочку с длинной ниточкой. Безо всяких дополнительных источников энергии ниточка вытянется так, как указано Н. Е. Жуковским. И этот замечательный ФАКТ, полученный экспериментаторами, может быть использован в качестве граничного условия теоретиками.

• "Циркуляции вектора скорости вокруг профилей крыльев на Вашем среднем рисунке и на моих рисунках 2 и 3 равны нулю (и никаких «присоединенных вихрей» там нет)."

Почему Вы так решили? Циркуляцию нужно измерять экспериментально либо рассчитывать по итогам решения, хотя бы, уравнений Рейнольдса.

• "Я многократно приводил пример о невозможности объяснить в рамках постулата Ж-Ч-К возникновение сил, необходимых для плавания рыб при поперечных движениях хвостом", "Вы ... не хотите признавать, что эта модель не сможет объяснить большинство результатов в инженерной практике"

НЕЖ, насколько мне известно, не предлагал объяснять плавание рыб при помощи данного постулата. Условия, сформулированные в постулате не выполняются => он не применим. Я лишь указывал, что в постулате не говорится ничего вроде =="настоящим постулатом запрещается рыбам плавать, а птицам летать"==

• "Вы упорно отказываетесь признавать не только противоречие модели Жуковского-Кутта закону сохранения энергии"

Верно одно из двух - либо теория (закон сохранения энергии) соответствует экспериментальному факту (постулату Жуковского) либо нет. В любом случае, несоответствие ФАКТа теории не есть повод для отмены факта - скорее это повод для корректировки теории. От себя замечу - предо мной подобная проблема не стоит, ибо я верую и в закон и в постулат.

• "противоречие статей в ВИКИПЕДИИ базовым физическим законам – это несовместимо с определением «ЭНЦИКЛОПЕДИЯ»"

О принципах отбора материала для Вики уже писалось. Но, коль скоро мы договорились, что "постулат" = "аксиома", хочу указать, что попытки исключить данную статью равноценны попыткам исключить аксиомы Евклида из курса геометрии при помощи ссылок на Лобачевского. 8))

С уважением, Iatsouk 21:48, 9 января 2009 (UTC)

__________________

Уважаемый участник Iatsouk. Ваши возражения постоянно противоречат Вашим же словам и рисункам.

Вы «отрицаете возможность появления вихрей, ось которых направлена ВДОЛЬ кромки (при малых углах атаки), вихри, ось которых направлена под прямым углом к кромке - ОБЯЗАНЫ ПРИСУТСТВОВАТЬ в случае крыла конечного размаха». – Однако, на Вашем среднем рисунке (в предыдущих замечаниях) за профилем крыла присутствуют вихри, ось которых «направлена ВДОЛЬ кромки». Более того, отличная от нуля циркуляция вектора скорости вокруг профиля крыла при безвихревом безотрывном обтекании (или как Вы ее называете «присоединенный вихрь») на Вашем верхнем рисунке также имеет ось, «направленную ВДОЛЬ кромки». На моих рисунках 2 и 3, а также на предложенной Вами фотографии гребного винта с отрывом струй (http://en.wiki.x.io/wiki/Ship_model_basin) отличный от нуля вектор ротора скорости на вихревых поверхностях тангенциального разрыва также направлен параллельно кромкам. Вы уж как-то определитесь: отрицаются такие вихри, или нет?!

Ваше высказывание: «Не скажу про самолетные крылья, а вот про лопасти винта знаю точно - углы атаки сечений лопасти составляют 1...3 градуса» – также противоречит указанной фотографии гребного винта в кавитационной трубе. На этой фотографии углы атаки лопастей винта на порядок больше (и даже больше, чем 10…15 градусов). Возможно, произошла опечатка в Вашем ответе. Хотел бы я посмотреть на фотографию гребного винта с практически нулевыми (т.е. всего лишь 1…3 градуса) углами атаки.

Ваше высказывание: «Полное давление = статическое + динамическое, и даже, если динамическое отрицательно, сумма будет больше нуля» – как-то не стыкуется с уравнением Бернулли, которое указывает, что вдоль линии тока выполняется равенство: p + (ρ * V^2 / 2) + ρ* g * z = const . В левой части равенства кроме статического давления (p) имеется компонента (ρ* V^2 / 2), которую называют «скоростной напор», а также компонента (ρ* g * z), которую называют «вертикальный напор». Если линия тока расположена горизонтально, т.е. z = const, то и вертикальный напор можно перенести в правую часть равенства. Поэтому для горизонтальных линий тока уравнение Бернулли имеет вид: p + (ρ* V^2 / 2) = const. Возможно, Вы называете «скоростной напор» (ρ* V^2 / 2) динамическим давлением? Но эта компонента не может стать отрицательной, потому что квадрат скорости – всегда величина положительная.

Ваша фраза: «Вблизи лопастей тяжелонагруженных судовых гребных винтов часто наблюдается явление кавитации - образование каверн, заполненных парами жидкости» – также не доказывает существование отрицательных давлений, потому что внутри каверн давление паров жидкости, хотя и маленькое, но больше нуля, т.е. положительное. Вы должны признать, что нулевое давление может быть только в вакууме. Но тогда какая модель может описать отрицательное давление? Что может быть меньше вакуума?

В Вашем описании эксперимента: «Вот в этой трубе для того, чтобы увидеть постулат Жуковского-Чаплыгина своими глазами достаточно поставить в рабочую часть крылышко, нажать кнопочку на пульте и взять в руки указочку с длинной ниточкой. Безо всяких дополнительных источников энергии ниточка вытянется так, как указано Н. Е. Жуковским» – имеется СУЩЕСТВЕННАЯ МЕТОДИЧЕСКАЯ ПОГРЕШНОСТЬ – а именно: нельзя использовать «длинную ниточку». Ниточка должна быть ЗНАЧИТЕЛЬНО короче (раз в 5…10) размеров «крылышка». И тогда Вы сможете воочию наблюдать при «точечных» замерах короткой ниточкой отрывы струй и поверхности тангенциального разрыва за профилем «крылышка» и никакой отличной от нуля циркуляции вокруг профиля крылышка не будет.

Вы называете постулат Ж-Ч «экспериментальным фактом», но все эксперименты опровергают модель безвихревого безотрывного обтекания твердых тел. Предложенная Вами фотография гребного винта с отрывом струй (http://en.wiki.x.io/wiki/Ship_model_basin) подтверждает модель Кирхгофа и опровергает постулат Ж-Ч. Плавание рыб можно объяснить вихревой моделью Кирхгофа, но нельзя объяснить безотрывной моделью Жуковского-Чаплыгина-Кутта. Парус при боковом ветре обеспечивает движение парусника даже перпендикулярно вектору скорости ветра, и никакая безвихревая безотрывная модель обтекания паруса не может этого объяснить. На моем рис. 3 показан пример возникновения подъемной силы при обтекании профиля с передней острой кромкой, и это легко проверить экспериментально, а постулат Ж-Ч этого объяснить не может. Плоский воздушный змей с двумя острыми кромками сотни лет запускают даже маленькие дети, а взрослые дяди Жуковский и Чаплыгин утверждают, что этот змей летать не должен, так как невозможно обеспечить безвихревое безотрывное обтекание.

Вы фанатично «веруете в постулат» о безвихревом безотрывном обтекании, но только при очень маленьких скоростях потока (потому что при увеличении скорости потока обязательно возникает отрыв струй, как на предложенной Вами фотографии гребного винта), и только при маленьких углах атаки (но на предложенной Вами фотографии гребного винта углы атаки больше 10…15 градусов), и только при выполнении условия Кутта о передней закругленной кромке и острой задней кромке (но лопасти гребных винтов имеют острые и переднюю и заднюю кромки). Все экспериментальные результаты противоречат Вашей «фанатичной вере».

Отвечу второму участнику обсуждения – метод Кирхгофа и метод Кармана хорошо описаны в учебнике: Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидродинамика. Ч.1./ Под ред. И.А. Кибеля. Издание шестое.- М.: Гос. из-во физ.-мат. лит., 1963.

К сожалению я не нашел в Интернете электронную версию этой книги. Но наверняка есть и другие, более современные учебники с описаниями этих методов (справедливости ради необходимо отметить, что таких учебников очень мало).

С уважением Alexandr_AUGUST 212.111.199.50 08:02, 19 января 2009 (UTC)

____________

Уважаемый участник Iatsouk. Если Вас не убедили приведенные ранее доказательства противоречий экспериментальных результатов постулату Жуковского-Чаплыгина-Кутта, привожу пример противоречий этого постулата закону сохранения энергии (конкретно – теореме Лагранжа).

Повторюсь еще раз: в теоремах Кельвина (Томсона) и Лагранжа доказана «неизменность циркуляции скорости (или неизменность вихря скорости) во всех точках баротропно движущейся идеальной среды под действием объемных сил с однозначным потенциалом». То есть по условию этих теорем для поддержания неизменности циркуляции вектора скорости или неизменности вихря скорости (в частном случае, для теоремы Лагранжа – циркуляция или вихрь скорости остаются нулевыми) необходимо, чтобы в идеальной движущейся среде отсутствовала диссипация (т.е. среда является баротропной) и в потоке отсутствовали источники энергии – движение происходит по инерции (если движение происходит по горизонтали, и гравитационные силы не участвуют в расчетах, то единственная объемная или массовая сила – это сила инерции).

В некоторых учебниках по аэро-гидро-динамике для оправдания постулата Жуковского-Чаплыгина-Кутта приводятся утверждения типа: «Теорема Лагранжа о нулевой циркуляции справедлива только для односвязных контуров, а для многосвязных контуров эта теорема неприменима». Односвязными контурами называют такой контур, который при постепенном уменьшении размеров может стянуться в точку. Если внутри контура имеются твердые тела, то такие контура называются многосвязными и при уменьшении размеров контура не могут стянуться в точку, а будут охватывать твердое тело.

Такое разделение закона сохранения энергии – отдельный закон сохранения энергии для односвязных контуров и отдельный закон для многосвязных контуров – является абсурдным. Но в приведенных ниже доказательствах исходным положением является теорема Лагранжа для односвязных контуров – и доказана справедливость этой теоремы для многосвязных контуров.

На рис. 5 показано безвихревое безотрывное обтекание идеальной средой профиля твердого тела в соответствии с постулатом Жуковского-Чаплыгина-Кутта. Выделим вокруг твердого тела на значительном расстоянии (на котором уже незаметно искривление линий тока за счет обтекания твердого тела) прямоугольный контур ABCD. Грани AB и CD этого контура совпадают с первоначальным направлением вектора скорости потока, а грани DA и BC – перпендикулярны вектору скорости потока.

Циркуляцию вектора скорости (Г) по контуру ABCD на рис. 5 можно представить как сумму линейных интегралов (ЛИ) по четырем граням этого контура: Г (ABCD) = ЛИ (AB) + ЛИ (BC) + ЛИ (CD) + ЛИ (DA).

Напомню: линейный интеграл (ЛИ) вычисляется как произведение вектора элементарного (бесконечно малого) фрагмента кривой на вектор скорости в этой точке и на косинус угла между ними. Потом эти элементарные произведения интегрируются вдоль всего отрезка кривой. Из рис. 5 можно сделать вывод о том, что: ЛИ (BC) = 0 и ЛИ (DA) = 0, т.к. косинус угла 90 градусов равен нулю, а ЛИ (AB) = – ЛИ (CD), т.к. длины отрезков равны и обходятся по контуру встречно. Поэтому циркуляция вектора скорости по контуру ABCD равна нулю (хотя этот контур является многосвязным), что соответствует теореме Лагранжа.

Проведем к твердому телу от контура ABCD отрезки EF и HK параллельно граням DA и BC (см. рис. 5). В соответствии с теоремой Лагранжа при отсутствии источников энергии циркуляции вектора скорости вдоль односвязных контуров Г (AEFLHKD) и Г (BCKHMFE) равны нулю. При обходе этих контуров по часовой стрелке (но можно обходить и против часовой стрелки) рассчитаем сумму циркуляций по этим двум контурам как сумму линейных интегралов (ЛИ) по отрезкам этих контуров:

Г (AEFLHKD) + Г (BCKHMFE) = [ ЛИ (DA) + ЛИ (AE) + ЛИ (EF) + ЛИ (FLH) + ЛИ (HK) + ЛИ (KD) ] + [ ЛИ (ЕВ) + ЛИ (BC) + ЛИ (СК) + ЛИ (KH) + ЛИ (HMF) + ЛИ (FE) ].

Из этого равенства можно сделать вывод о том, что сумма циркуляций вдоль этих контуров равна циркуляции вектора скорости по контуру твердого тела Г (FMHL), потому что: ЛИ (DA) = ЛИ (BC) = 0 (косинус прямого угла равен нулю), ЛИ (AE) = – ЛИ (KD), ЛИ (ЕВ) = – ЛИ (СК), а также ЛИ (EF) = – ЛИ (FE), ЛИ (HK) = – ЛИ (KH), т.к. эти смежные отрезки в двух контурах обходятся встречно.

И заключительный естественный результат: если каждая из циркуляций по односвязным контурам Г (AEFLHKD) и Г (BCKHMFE) равны нулю, то и сумма этих циркуляций равна нулю, т.е. равна нулю циркуляция вектора скорости по многосвязному контуру вокруг твердого тела Г (FMHL). Такой нулевой результат можно было предсказать до начала этих геометрических рассуждений на основании теоремы Лагранжа.

Обратите внимание: нулевая циркуляция вдоль контура твердого тела заложена уже на начальном этапе при выборе модели безвихревого безотрывного обтекания идеальной средой твердого тела. Причем форма этого твердого тела и угол атаки не влияют на конечный нулевой результат. Острые или закругленные кромки могут быть спереди или сзади, но циркуляция вектора скорости всегда равна нулю.

Ваша фанатичная «вера в постулат Ж-Ч-К» противоречит как экспериментальным результатам, так и теоретическим расчетам. В парадоксе Д’Аламбера-Эйлера (а этому парадоксу уже более 260 лет) показано, что при выборе модели безвихревого безотрывного обтекания идеальной средой твердого тела все циркуляции вектора скорости, все вихри равны нулю и все силы взаимодействия твердого тела с идеальной средой равны нулю. В постулате Ж-Ч-К после выбора модели безвихревого безотрывного обтекания (как и в парадоксе Д-Э) все циркуляции должны быть равны нулю (в соответствии с законом сохранения энергии) и никакого силового взаимодействия твердого тела с идеальной средой в принципе быть не может.

Поэтому для объяснения причин возникновения лобовой или ортогональных сил при движении твердого тела в идеальной среде необходимо использовать модели обтекания твердых тел с вихреобразованием (модель Кирхгофа-Гельмгольца, модель Кармана и др.), необходимо вводить в поток источники энергии и тогда получаются теоретические результаты, адекватно совпадающие с экспериментальными данными и не противоречащие теореме Лагранжа и закону сохранения энергии.

Я все еще надеюсь на взаимопонимание и на консенсус по обсуждаемым вопросам. С уважением Alexandr AUGUST 09:56, 14 февраля 2009 (UTC)

---

---

     2010  --  ГОД  ТИГРА  --  2010
          --------------------------------------
                       -------------------------

Вот и наступил новый 2010-й год. С чем и поздравляю всех читателей ВИКИПЕДИИ .

За прошедший год никто не захотел (или не сумел) замолвить доброе слово за теорему Жуковского-Кутта. Поэтому пора подводить итоги.

Собственно это обсуждение закончилось тем же, с чего и началось - ТЕОРЕМА ЖУКОВСКОГО-КУТТА и ПАРАДОКС Д’АЛАМБЕРА-ЭЙЛЕРА – это всего лишь теоретические недоразумения, возникшие на этапе абстрактных рассуждений из-за неправильно выбранных начальных условий. Результаты таких теоретических расчетов с нулевой силой лобового сопротивления НИКОГДА не будут реализованы на практике.

Выбирая на начальном этапе теоретических вычислений модель безвихревого безотрывного обтекания идеальной средой твердых тел, можно далее особо не напрягаться – полученный результат все равно будет с НУЛЕВЫМИ СИЛОВЫМИ ВЗАИМОДЕЙСТВИЯМИ ИДЕАЛЬНОЙ СРЕДЫ С ТВЕРДЫМИ ТЕЛАМИ (в соответствии с законом сохранения энергии). Более того, получив в результате теоретических расчетов отличную от нуля силу, можно быть уверенным – где-то в расчетах вкралась ошибочка или нарушен закон сохранения энергии (что также является грубейшей ошибкой).

Конкретный пример нарушения закона сохранения энергии – это постулат Жуковского-Чаплыгина-Кутта о возникновении отличной от нуля циркуляции при установившемся (стационарном) безвихревом, безотрывном обтекании идеальной средой твердых тел без внешних источников энергии. Ну не может возникнуть отличная от нуля циркуляция (т.е. дополнительная кинетическая энергия в потоке) сама по себе – «по щучьему велению, по моему хотению»!!! Необходим внешний источник энергии.

Причем величина и направление этой циркуляции в постулате Жуковского-Чаплыгина-Кутта определяются только углом атаки (т.е. геометрическим параметром) твердого тела относительно начального вектора скорости движения идеальной среды – без дополнительных источников энергии такие рассуждения являются полнейшим абсурдом.

Но не все так плачевно. Можно найти и положительный полезный момент - математическая формула теоремы Жуковского-Кутта позволяет рассчитывать величину подъемной силы (в общем случае – ортогональной силы) для эффекта Магнуса. И только в этой роли теорема Жуковского-Кутта останется в памяти потомков и теоретической аэродинамике.

А для расчета подъемной силы и силы лобового сопротивления существуют альтернативные модели обтекания идеальной средой твердых тел с вихреобразованием (модель Кирхгофа-Гельмгольца, модель Кармана и др.). Полученные теоретические результаты вполне адекватно совпадают с реальными физическими процессами. И не нужно высасывать из пальца «отличную от нуля циркуляцию» и прочие абсурды.

Единственная досадная проблема заключается в том, что в ВИКИПЕДИИ я не нашел описание «метода Кирхгофа» и других методов обтекания идеальной средой твердых тел с вихреобразованием. Имеется только биография Г.Р. Кирхгофа, в которой два слова сказано о том, что: «Свои взгляды на основные принципы механики Кирхгоф изложил в весьма известных лекциях по механике, содержащих и решение множества трудных вопросов теорий упругости и течения жидкости».

Уделив внимание в ВИКИПЕДИИ абсурдной теореме Жуковского-Кутта, надо бы подготовить статьи и об альтернативных моделях. Это большой укор модераторам энциклопедии.

Еще раз поздравляю всех с новым годов и желаю новых творческих успехов в НОВОМ ГОДУ.

Alexandr AUGUST  212.111.199.50 07:27, 15 января 2010 (UTC)

Здесь не форум, а Википедия - не трибуна. Отстаивайте справедливость в других местах, или доказывайте их приведением ссылок на авторитетные источники. В вузах эта теорема изучается, и это непреложный факт. А модель Кирхгофа-Гельмгольца, модель Кармана и др. вы можете написать сами и модераторы тут ни при чём: Википедия - добровольный проект. Удачи! infovarius

Off topic

Уважаемый Alexandr AUGUST

В русскоязычном сегмент I-net'а практически не выложено учебников по аэродинамике. Те, что есть - обычно, в невероятно неудобном формате .djv

В такой ситуации, я думаю, было бы очень хорошо, если бы Вы сделали на своем сайте раздел, посвященный вихрям Кирхгофа. Я не знаю, в какой форме это следует делать: конвертировать тексты учебников, писать собственные заметки, объясняющие, о чем идет речь "на пальцах". Если говорить о вихрях, то там, вообще, очень много занятного: от дорожки Кармана до "игры" вихревых колец.

Я полагаю, что очень многим людям (и, в первую очередь, мне) подобный сайт был бы весьма интересен.

Примечание.

Создание популярной заметки о методе вихрей Кирхгофа - большой труд, поэтому я намеренно не предлагаю писать ее в Википедии. Во-первых, из-за анонимности, и, во-вторых, текст может погибнуть при неудачном редактировании. Однако, в Википедию можно скопировать готовый вариант.

220.240.104.36 00:41, 10 января 2009 (UTC)biglebowsky.livejournal.com

Пробел в начале строки здесь означает преформатированный текст - лучше его не ставить. infovarius 12:44, 21 января 2009 (UTC)

Спасибо за объяснение и исправление ошибки форматирования.--Biglebowsky 14:06, 23 января 2009 (UTC)

Re: Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидродинамика. Александр, спасибо. --Biglebowsky 14:10, 23 января 2009 (UTC)

_____________

Я уже предлагал в начале этого обсуждения познакомиться с моей статьей на сайте : http://dalamberparadox.narod.ru/ В этой статье также описан "на пальцах" и метод Кирхгофа-Гельмгольца.

С уважением Alexandr_AUGUST 212.111.199.50 06:38, 2 февраля 2009 (UTC)