Мультивектор

Мультивектор — элемент внешней алгебры, представляющий собой сумму поливекторов (векторов, бивекторов, тривекторов и т. д.).

Сумма 2-мультивекторов

Любой поливектор (k-вектор) можно представить как сумму k-лезвий (простых k-векторов), где каждое k-лезвие в свою очередь разложимо на внешнее произведение векторов количеством k штук.

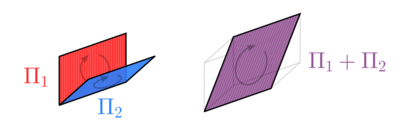
2-лезвие может быть геометрически представлено как ориентированная плоскость в пространстве любой размерности и может использоваться для представления вращения в нём.

n-вектор в пространстве размерности n называется псевдоскаляром, тогда как (n-1)-вектор называется псевдовектором. Так, псевдовектором трёхмерного пространства является любой бивектор.

Сумма 1-вектора и скаляра также известна как паравектор.

k-вектор дуален к k-форме.

Свойства:

• Любая линейно независимая система векторов $a_{1},a_{2},\dots ,a_{k}$ из $V$ определяет ненулевой k-вектор;
• Линейно независимые системы $a_{1},a_{2},\dots ,a_{k}$ и $b_{1},b_{2},\dots ,b_{k}$ порождают одно и то же подпространство в $V$ в том и только в том случае, когда
      $a_{1}\wedge a_{2}\wedge \dots \wedge a_{k}=\lambda b_{1}\wedge b_{2}\wedge \dots \wedge b_{k}$;
• Для любого ненулевого поливектора $t\in \bigwedge \nolimits ^{k}V$ его аннулятор $\operatorname {Ann} t=\{v\in V|t\wedge v=0\}$ есть подпространство размерности $\leq k$, причём поливектор $t$ разложим тогда и только тогда, когда $\dim \operatorname {Ann} t=k$;
• Разложимые k-векторы n-мерного пространства V образуют коническое алгебраическое многообразие в $\Lambda ^{k}(V)$ соответствующее проективное алгебраическое многообразие есть многообразие Грассмана;
• Любой ненулевой n-вектор или (n − 1)-вектор в n-мерном пространстве разложим;
• Бивектор $t$ разложим тогда и только тогда, когда $t\wedge t=0$;
• Если фиксировать ненулевой $n$-вектор $\omega \in \bigwedge \nolimits ^{n}(V)$, то возникает естественный изоморфизм:

  $\pi :\bigwedge \nolimits ^{k}(V)\to \bigwedge \nolimits ^{n-k}(V)$

  такой, что $t\wedge u=\langle \pi (t),u\rangle \omega$ для всех $u\in \bigwedge \nolimits ^{n-k}(V)$.

Литература

• Кострикин А. П., Манин Ю. И. Линейная алгебра и геометрия (недоступная ссылка). — М.: Наука, 1980.
• Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия. — М.: Физматлит, 2009.