Кубическая функция

Куби́ческая фу́нкция в математике — это числовая функция $f:\mathbb {R} \to \mathbb {R}$ вида

f(x)=ax^{3}+bx^{2}+cx+d,\quad x\in \mathbb {R} ,

где $a\neq 0.$ Другими словами, кубическая функция задаётся многочленом третьей степени.

Аналитические свойства

Производная кубической функции $f(x)=ax^{3}+bx^{2}+cx+d$ имеет вид $f'(x)=3ax^{2}+2bx+c$ . В случае, когда дискриминант ${\frac {D}{4}}=b^{2}-3ac$ полученного квадратного уравнения $f'(x)=0$ больше нуля, оно имеет два различных решения, которые соответствуют критическим точкам функции $f$ . При этом, одна из этих точек является точкой локального минимума, а другая точкой локального максимума. Равенство нулю второй производной $f''$ определяет точку перегиба $x=-b/3a$ .

График

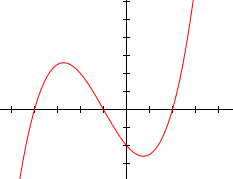
График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции $y=ax^{3}$ или $y=x^{3}$ . Легко видеть, что, применяя параллельный перенос, можно привести кубическую параболу к виду, когда она будет задаваться уравнением $y=ax^{3}-px$ . Путём применения аффинных преобразований плоскости можно добиться, чтобы $a=1$ и $p=0$ . В этом смысле все определения будут эквивалентны.

Кроме того, кубическая парабола

центрально-симметрична относительно точки перегиба,
всегда пересекает линию абсцисс хотя бы в одной точке,
не имеет общих точек со своей касательной в точке перегиба, кроме как в самой точке касания.

**Поведение графика при изменении коэффициентов**

Коэффициент при кубе	Коэффициент при квадрате	Коэффициент при первой степени

Коллинеарность

Касающиеся прямые в трёх коллинеарных точках графика кубической функции пересекают график снова в коллинеарных точках.^[1]

Применение

Кубическую параболу иногда применяют для расчёта переходной кривой на транспорте, так как её вычисление намного проще, чем построение клотоиды.

См. также

Примечания

↑ Whitworth, William Allen. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions, Forgotten Books, 2012 (orig. Deighton, Bell, and Co., 1866). http://www.forgottenbooks.com/search?q=Trilinear+coordinates&t=books Архивная копия от 24 марта 2016 на Wayback Machine

Литература

Л. С. Понтрягин, Кубическая парабола // «Квант», 1984, № 3.
И. Н. Бронштейн, К. А. Семендяев, «Справочник по математике», издательство «Наука», М. 1967, с. 84

[1] Whitworth, William Allen. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions, Forgotten Books, 2012 (orig. Deighton, Bell, and Co., 1866). http://www.forgottenbooks.com/search?q=Trilinear+coordinates&t=books Архивная копия от 24 марта 2016 на Wayback Machine

[1]