Дерево палиндромов (англ. palindromic tree, также овердрево[1], англ. eertree) — структура данных, предназначенная для хранения и обработки палиндромных подстрок некоторой строки. Была предложена учёными из Уральского федерального университета Михаилом Рубинчиком и Арсением Шуром в 2015 году. Представляет собой два префиксных дерева, собранных из правых «половинок» палиндромных подстрок чётной и нечётной длины соответственно. Структура занимает памяти и может быть построена за время , где — длина строки, а — количество различных символов в ней. С помощью дерева палиндромов можно эффективно решать такие задачи, как подсчёт числа различных палиндромных подстрок, поиск разбиения строки на наименьшее число палиндромов, проверка подстроки на то, является ли она палиндромом, и другие.
| Дерево палиндромов | |||||||
|---|---|---|---|---|---|---|---|
| англ. eertree | |||||||
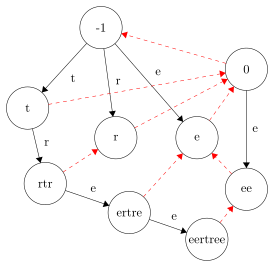 Дерево палиндромов для строки eertree | |||||||
| Тип | структура данных | ||||||
| Год изобретения | 2015 | ||||||
| Автор | Михаил Рубинчик[вд] | ||||||
| Сложность в О-символике | |||||||
|
|||||||
Обозначения
правитьПусть — некоторая строка, а — обращённая строка . При описании дерева палиндромов строки используются следующие обозначения[2]:
- Строка называется палиндромом, если она читается одинаково слева направо и справа налево, то есть если .
- Подстрокой называют непрерывную подпоследовательность строки и обозначают .
- В частности, подстрока, у которой , называется префиксом строки , а подстрока, у которой , — суффиксом строки .
- Палиндромной подстрокой (подпалиндромом) называют подстроку , которая является палиндромом. Если эта подстрока также является префиксом или суффиксом строки , то её называют префикс- или суффикс-палиндромом соответственно.
- Префиксным деревом называют корневое ориентированное дерево, дуги которого помечены символами таким образом, что из любой вершины этого дерева исходит не больше одной дуги, помеченной данным символом.
- Каждой вершине префиксного дерева соответствует строка, равная конкатенации символов на пути из корня дерева в эту вершину.
Структура дерева
правитьВ обозначениях выше, дерево палиндромов строки — это ориентированный граф, каждая вершина которого соответствует некоторому уникальному подпалиндрому строки и отождествляется с ним. Если у строки есть подпалиндромы и , где — некоторый символ алфавита, то в дереве палиндромов есть дуга, помеченная символом , из вершины, соответствующей , в вершину, соответствующую . В таком графе у любой вершины может быть только одна входящая дуга. Для удобства также вводятся две служебные вершины, которые соответствуют палиндромам длины (пустая строка) и («мнимая» строка) соответственно. Дуги из пустой строки ведут в вершины, соответствующие палиндромам вида , а из «мнимой строки» — в вершины, соответствующие палиндромам вида (то есть состоящим из единственного символа). Вершина называется чётной, если ей соответствует палиндром чётной длины, и нечётной в противном случае. Из определения следует, что дуги в дереве палиндромов проходят только между вершинами с одинаковой чётностью. С точки зрения префиксных деревьев данная структура может быть описана следующим образом[3]:
Вершины и дуги дерева палиндромов образуют два префиксных дерева, корни которых находятся в вершинах, задающих пустую и «мнимую» строки соответственно. При этом первое префиксное дерево составлено из правых половин подпалиндромов чётной длины, а второе — нечётной.
Количество вершин в дереве палиндромов не превосходит , что является прямым следствием следующей леммы[4]:
У строки длины может быть не больше различных непустых палиндромных подстрок. Более того, после приписывания некоторого символа в конец строки количество различных подпалиндромов данной строки может увеличиться не больше, чем на .
Данное утверждение следует из следующих фактов:
- Если палиндром — суффикс палиндрома , то он также является его префиксом;
- Если палиндромы и — суффиксы строки и , то встречается в хотя бы два раза (как префикс и как суффикс );
- У любой строки может быть не больше одного уникального (встречающегося в всего один раз) суффикс-палиндрома.
Последнее свойство по сути эквивалентно лемме, так как все новые подстроки, которые появляются при дописывании очередного символа к строке, должны быть её суффиксами[5].■
Помимо обычных дуг, которые служат переходами для префиксного дерева, для каждой вершины дерева палиндромов определяется суффиксная ссылка, которая ведёт из вершины в вершину , соответствующую наибольшему собственному (не равному всей строке ) суффикс-палиндрому . При этом суффиксная ссылка из «мнимой» вершины не определена, а из пустой вершины по определению ведёт в «мнимую». Суффиксные ссылки образуют дерево с корнем в «мнимой» вершине и играют важную роль в построении дерева палиндромов[3].
Построение
правитьКак и многие другие строковые структуры, дерево палиндромов строится итеративно. Изначально оно состоит лишь из вершин, соответствующих пустой и мнимой строкам. Затем структура постепенно перестраивается при наращивании строки по одному символу. Так как при добавлении одного символа в строке появляется не более одного нового палиндрома, перестройка дерева в худшем случае потребует добавления одной новой вершины и суффиксной ссылки к ней. Для определения возможной новой вершины в ходе построения дерева поддерживается указатель last на вершину, соответствующую наибольшему из текущих суффикс-палиндромов[3].
Все суффикс-палиндромы строки достижимы по суффиксным ссылкам из last, поэтому для определения нового суффикс-палиндрома (именно он будет соответствовать новой вершине, если таковая появится) необходимо переходить по суффиксным ссылкам last, пока не обнаружится, что символ, предшествующий текущему суффикс-палиндрому, совпадает с символом, который был приписан к строке. Более формально, пусть — максимальный суффикс-палиндром строки , тогда либо , либо , где — некоторый суффикс-палиндром . Таким образом, перебирая среди суффиксных ссылок last, можно определить, может ли он быть расширен до путём сравнения символов и . Когда соответствующий суффикс-палиндром был найден, следует проверить, присутствует ли в дереве палиндромов переход из соответствующей ему вершины по символу [3].
Если такой переход есть, то уже встречался в строке ранее и соответствует вершине, в которую ведёт этот переход. В противном случае необходимо создать для него новую вершину и провести переход по из . Затем следует определить суффиксную ссылку для , которая соответствует второму максимальному суффикс-палиндрому . Для того, чтобы её найти, следует продолжать обход суффиксных ссылок last, пока не встретится вторая вершина , такая что ; именно эта вершина и будет суффиксный ссылкой . Если обозначить переход из вершины по символу как , весь процесс может быть описан следующим псевдокодом[3]:
функция find_link(v): пока sk-len(v)-1 ≠ sk: присвоить v = link(v) вернуть v функция add_letter(c): присвоить k = k + 1 определить sk = c определить q = find_link(last) если δ(q, c) не определено: определить p = new_vertex() определить len(p) = len(q) + 2 определить link(p) = δ(find_link(link(q)), c) определить δ(q, c) = p присвоить last = δ(q, c)
Здесь предполагается, что изначально дерево описывается лишь двумя вершинами с длинами и соответственно с суффиксной ссылкой из первой вершины во вторую. В переменной last хранится вершина, соответствующая наибольшему суффикс-палиндрому текущей строки, изначально она указывает на вершину нулевой строки. Также предполагается, что изначально равно и в записан некоторый служебный символ, который не встречается в строке .
Вычислительная сложность
правитьСложность алгоритма может варьировать в зависимости от структур данных, в которых хранится таблица переходов в дереве. В общем случае при использовании ассоциативного массива время, затрачиваемое на обращение к , достигает , где — размер алфавита, из символов которого построена строка. Стоит заметить, что каждая итерация первого вызова find_link уменьшает длину last, а второго — длину link(last), которые между последовательными вызовам add_letter могут увеличиться только на единицу. Таким образом, суммарное время работы find_link не превосходит , а общее время, требуемое для выполнения вызовов add_letter, можно оценить как [3]. Расход памяти у данной структуры в худшем случае линейный, однако если рассматривать усреднённый размер структуры по всем строкам заданной длины , средний расход памяти будет порядка [6].
Модификации
правитьОдновременно с введением данной структуры данных Рубинчик и Шур также предложили ряд модификаций, позволяющих расширить область задач, решаемых деревом палиндромов. В частности, был предложен метод, позволяющий с той же асимптотикой построить общее дерево палиндромов для множества строк . Такая модификация позволяет решать те же задачи, рассматриваемые в контексте множества строк — например, найти наибольший общий подпалиндром всех строк или число различных подпалиндромов всех строк в совокупности. Другой предложенной модификацией стал вариант построения дерева, при котором на добавление одного символа требуется времени в худшем случае (а не амортизированно, как это происходит в стандартном построении) и памяти. Такой подход позволяет обеспечить частичную персистентность[англ.] дерева, при которой можно в произвольные моменты времени откатывать добавление последнего символа. Кроме того, была предложена полностью персистентная версия дерева, позволяющая обратиться и дописать символ к любой из сохранённых ранее версий за времени и памяти в худшем случае[7].
В 2019 году Ватанабе с коллегами разработали на основе дерева палиндромов структуру данных, называемую e2rtre2, для работы с подпалиндромами строк, заданных кодированием длин серий[4], а в 2020 году тот же состав авторов, совместно с Миено, разработали два алгоритма, позволяющих поддерживать дерево палиндромов на скользящем окне размера . Первый из указанных алгоритмов требует времени и памяти, а второй — времени и памяти[8].
Применения
правитьДерево палиндромов даёт множество возможных применений для получения теоретически быстрых и практически легко реализуемых алгоритмов для решения ряда комбинаторных задач в программировании и математической кибернетике[9].
Одной из задач, для которых была разработана данная структура, является подсчёт различных подпалиндромов в строке в режиме онлайн[англ.]. Она может быть поставлена следующим образом: к изначально пустой строке поочерёдно приписывается по одному символу. На каждом шаге необходимо вывести число различных подпалиндромов в данной строке. С точки зрения дерева палиндромов это эквивалентно тому, чтобы на каждом шаге вывести количество нетривиальных вершин в структуре. Линейное решение для оффлайн-версии данной задачи было представлено в 2010 году[10], а оптимальное решение со временем исполнения для онлайн-версии было найдено в 2013 году[11]. Указанное решение, однако, использовало две «тяжеловесные» структуры данных — аналог алгоритма Манакера, а также суффиксное дерево. Дерево палиндромов же, с одной стороны, имеет ту же асимптотику в худшем случае, а с другой — является значительно более легковесной структурой[3].
Другим возможным применением данной структуры является перечисление палиндромно-богатых двоичных строк[12]. Ранее было показано, что слово длины может содержать не более различных палиндромов, палиндромно-богатыми называются слова, на которых данная оценка достигается. Понятие палиндромно-богатых слов было введено Эми Глен и коллегами в 2008 году[13]. Рубинчик и Шур показали, что с помощью дерева палиндромов можно обнаружить все палиндромно-богатые слова, чья длина не превосходит за , где — количество таких слов. Данный результат позволил увеличить количество известных членов последовательности A216264 в OEIS c 25 до 60. Полученные данные показали, что последовательность растёт значительно медленнее, чем это предполагалось ранее, а именно она ограничена сверху как [14].
Примечания
править- ↑ Рубинчик, 2016, с. 6—9
- ↑ Rubinchik, Shur, 2018, pp. 1—2
- ↑ 1 2 3 4 5 6 7 Rubinchik, Shur, 2018, pp. 2—6
- ↑ 1 2 Watanabe et al., 2019, pp. 432—434
- ↑ Droubay et al., 2001, pp. 542—546
- ↑ Rubinchik, Shur, 2016, p. 1
- ↑ Rubinchik, Shur, 2018, p. 6—11
- ↑ Mieno et al., 2020
- ↑ Рубинчик, 2016, с. 75—76
- ↑ Groult, 2010
- ↑ Kosolobov et al., 2013
- ↑ последовательность A216264 в OEIS
- ↑ Glen et al., 2009
- ↑ Rukavicka, 2017
Литература
править- Рубинчик М. Вычислительная сложность некоторых задач обработки строк — Екатеринбург: УрФУ, 2016. — 83 с.
- Droubay X., Justin J., Pirillo G. Episturmian words and some constructions of de Luca and Rauzy (англ.) // Theoretical Computer Science — Elsevier BV, 2001. — Vol. 255, Iss. 1-2. — P. 539—553. — ISSN 0304-3975; 1879-2294 — doi:10.1016/S0304-3975(99)00320-5
- Groult R., Prieur É., Richomme G. Counting distinct palindromes in a word in linear time (англ.) // Information Processing Letters — Elsevier BV, 2010. — Vol. 110, Iss. 20. — P. 908—912. — ISSN 0020-0190; 1872-6119 — doi:10.1016/J.IPL.2010.07.018
- Kosolobov D., Rubinchik M., Shur A. M. Finding distinct subpalindromes online (англ.) // Prague Stringology Conference — Czech Technical University in Prague: 2013. — P. 63—69. — arXiv:1305.2540
- Mieno T., Watanabe K., Nakashima Y., Inenaga S., Bannai H., Takeda M. Computing Palindromic Trees for a Sliding Window and Its Applications (англ.) // ArXiv.org — 2020. — 14 p. — ISSN 2331-8422 — arXiv:2006.02134
- Rubinchik M., Shur A. M. The Number of Distinct Subpalindromes in Random Words (англ.) // Fundamenta Informaticae — IOS Press, 2016. — Vol. 145, Iss. 3. — P. 371—384. — ISSN 0169-2968; 1875-8681 — doi:10.3233/FI-2016-1366 — arXiv:1505.08043
- Rubinchik M., Shur A. M. Eertree (англ.): An efficient data structure for processing palindromes in strings // European Journal of Combinatorics / P. O. de Mendez, P. Rosenstiehl, É. C. de Verdière, A. Björner, F. Brenti, A. Brouwer, P. Cameron, R. Cordovil, D. Foata, P. Frankl et al. — Elsevier BV, 2018. — Vol. 68. — P. 249—265. — ISSN 0195-6698; 1095-9971 — doi:10.1016/J.EJC.2017.07.021 — arXiv:1506.04862
- Watanabe K., Nakashima Y., Inenaga S., Bannai H., Takeda M. Shortest Unique Palindromic Substring Queries on Run-Length Encoded Strings (англ.) // Lecture notes in computer science / G. Goos, J. Hartmanis, J. v. Leeuwen — Berlin, Heidelberg, New York City, London: Springer, 2019. — P. 430—441. — ISSN 0302-9743; 1611-3349 — doi:10.1007/978-3-030-25005-8_35 — arXiv:1903.06290
- Glen A., Justin J., Widmer S., Zamboni L. Q. Palindromic richness (англ.) // European Journal of Combinatorics / P. O. de Mendez, P. Rosenstiehl, É. C. de Verdière, A. Björner, F. Brenti, A. Brouwer, P. Cameron, R. Cordovil, D. Foata, P. Frankl et al. — Elsevier BV, 2009. — Vol. 30, Iss. 2. — P. 510—531. — ISSN 0195-6698; 1095-9971 — doi:10.1016/J.EJC.2008.04.006 — arXiv:0801.1656
- Rukavicka J. On the Number of Rich Words (англ.) // Lecture notes in computer science / G. Goos, J. Hartmanis, J. v. Leeuwen — Berlin, Heidelberg, New York City, London: Springer, 2017. — P. 345—352. — 8 p. — ISSN 0302-9743; 1611-3349 — doi:10.1007/978-3-319-62809-7_26 — arXiv:1701.07778
Ссылки
править- Дерево палиндромов. Вики-конспекты ИТМО.
Эта статья входит в число хороших статей русскоязычного раздела Википедии. |



