Двоичное дерево поиска
Двоичное дерево поиска (англ. binary search tree, BST) — двоичное дерево, для которого выполняются следующие дополнительные условия (свойства дерева поиска):
- оба поддерева — левое и правое — являются двоичными деревьями поиска;
- у всех узлов левого поддерева произвольного узла X значения ключей данных меньше либо равны, нежели значение ключа данных самого узла X;
- у всех узлов правого поддерева произвольного узла X значения ключей данных больше, нежели значение ключа данных самого узла X.
| Двоичное дерево поиска | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
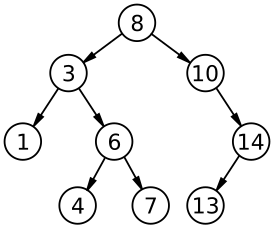 | ||||||||||||||||
| Тип | дерево | |||||||||||||||
| Год изобретения | 1960 | |||||||||||||||
| Автор | Andrew Donald Booth[вд] | |||||||||||||||
| Сложность в О-символике | ||||||||||||||||
|
||||||||||||||||
Очевидно, данные в каждом узле должны обладать ключами, на которых определена операция сравнения меньше либо равно.
Как правило, информация, представляющая каждый узел, является записью, а не единственным полем данных. Однако это касается реализации, а не природы двоичного дерева поиска.
Для целей реализации двоичное дерево поиска можно определить так:
- Двоичное дерево состоит из узлов (вершин) — записей вида (data, left, right), где data — некоторые данные, привязанные к узлу, left и right — ссылки на узлы, являющиеся детьми данного узла — левый и правый сыновья соответственно. Для оптимизации алгоритмов конкретные реализации предполагают также определения поля parent в каждом узле (кроме корневого) — ссылки на родительский элемент.
- Данные (data) обладают ключом (key), на котором определена операция сравнения «меньше». В конкретных реализациях это может быть пара (key, value) — (ключ, значение), или ссылка на такую пару, или простое определение операции сравнения на необходимой структуре данных или ссылке на неё.
- Для любого узла X выполняются свойства дерева поиска: key[left[X]] ≤ key[X] < key[right[X]], то есть ключи данных родительского узла нестрого больше ключей данных левого сына и меньше ключей данных правого.
Двоичное дерево поиска не следует путать с двоичной кучей, построенной по другим правилам.
Основным преимуществом двоичного дерева поиска перед другими структурами данных является возможная высокая эффективность реализации основанных на нём алгоритмов поиска и сортировки.
Двоичное дерево поиска применяется для построения более абстрактных структур, таких, как множества, мультимножества, ассоциативные массивы.
Основные операции в двоичном дереве поиска
правитьБазовый интерфейс двоичного дерева поиска состоит из трёх операций:
- FIND(K) — поиск узла, в котором хранится пара (key, value) с key = K.
- INSERT(K, V) — добавление в дерево пары (key, value) = (K, V).
- REMOVE(K) — удаление узла, в котором хранится пара (key, value) с key = K.
Этот абстрактный интерфейс является общим случаем, например, таких интерфейсов, взятых из прикладных задач:
- «Телефонная книжка» — хранилище записей (имя человека, его телефон) с операциями поиска и удаления записей по имени человека и операцией добавления новой записи.
- Domain Name Server — хранилище пар (доменное имя, IP адрес) с операциями модификации и поиска.
- Namespace — хранилище имён переменных с их значениями, возникающее в трансляторах языков программирования.
По сути, двоичное дерево поиска — это структура данных, способная хранить таблицу пар (key, value) и поддерживающая три операции: FIND, INSERT, REMOVE.
Кроме того, интерфейс двоичного дерева включает ещё три дополнительных операции обхода узлов дерева: INFIX_TRAVERSE, PREFIX_TRAVERSE и POSTFIX_TRAVERSE. Первая из них позволяет обойти узлы дерева в порядке неубывания ключей.
Поиск элемента (FIND)
правитьДано: дерево Т и ключ K.
Задача: проверить, есть ли узел с ключом K в дереве Т, и если да, то вернуть ссылку на этот узел.
Алгоритм:
- Если дерево пусто, сообщить, что узел не найден, и остановиться.
- Иначе сравнить K со значением ключа корневого узла X.
- Если K=X, выдать ссылку на этот узел и остановиться.
- Если K>X, рекурсивно искать ключ K в правом поддереве Т.
- Если K<X, рекурсивно искать ключ K в левом поддереве Т.
Добавление элемента (INSERT)
правитьДано: дерево Т и пара (K, V).
Задача: вставить пару (K, V) в дерево Т (при совпадении K, заменить V).
Алгоритм:
- Если дерево пусто, заменить его на дерево с одним корневым узлом ((K, V), null, null) и остановиться.
- Иначе сравнить K с ключом корневого узла X.
- Если K>X, рекурсивно добавить (K, V) в правое поддерево Т.
- Если K<X, рекурсивно добавить (K, V) в левое поддерево Т.
- Если K=X, заменить V текущего узла новым значением.
Удаление узла (REMOVE)
правитьДано: дерево Т с корнем n и ключом K.
Задача: удалить из дерева Т узел с ключом K (если такой есть).
Алгоритм:
- Если дерево T пусто, остановиться;
- Иначе сравнить K с ключом X корневого узла n.
- Если K>X, рекурсивно удалить K из правого поддерева Т;
- Если K<X, рекурсивно удалить K из левого поддерева Т;
- Если K=X, то необходимо рассмотреть три случая.
- Если обоих детей нет, то удаляем текущий узел и обнуляем ссылку на него у родительского узла;
- Если одного из детей нет, то значения полей ребёнка m ставим вместо соответствующих значений корневого узла, затирая его старые значения, и освобождаем память, занимаемую узлом m;
- Если оба ребёнка присутствуют, то
- Если левый узел m правого поддерева отсутствует (n->right->left)
- Копируем из правого узла в удаляемый поля K, V и ссылку на правый узел правого потомка.
- Иначе
- Возьмём самый левый узел m, правого поддерева n->right;
- Скопируем данные (кроме ссылок на дочерние элементы) из m в n;
- Рекурсивно удалим узел m.
- Если левый узел m правого поддерева отсутствует (n->right->left)
Обход дерева (TRAVERSE)
правитьЕсть три операции обхода узлов дерева, отличающиеся порядком обхода узлов.
Первая операция — INFIX_TRAVERSE — позволяет обойти все узлы дерева в порядке возрастания ключей и применить к каждому узлу заданную пользователем функцию обратного вызова f, операндом которой является адрес узла. Эта функция обычно работает только с парой (K, V), хранящейся в узле. Операция INFIX_TRAVERSE может быть реализована рекурсивным образом: сначала она запускает себя для левого поддерева, потом запускает данную функцию для корня, потом запускает себя для правого поддерева.
- INFIX_TRAVERSE (tr) — обойти всё дерево, следуя порядку (левое поддерево, вершина, правое поддерево). Элементы по возрастанию
- PREFIX_TRAVERSE (tr) — обойти всё дерево, следуя порядку (вершина, левое поддерево, правое поддерево). Элементы, как в дереве
- POSTFIX_TRAVERSE (tr) — обойти всё дерево, следуя порядку (левое поддерево, правое поддерево, вершина). Элементы в обратном порядке, как в дереве
В других источниках эти функции именуются inorder, preorder, postorder соответственно[1]
- INFIX_TRAVERSE
Дано: дерево Т и функция f
Задача: применить f ко всем узлам дерева Т в порядке возрастания ключей
Алгоритм:
- Если дерево пусто, остановиться.
- Иначе
- Рекурсивно обойти левое поддерево Т.
- Применить функцию f к корневому узлу.
- Рекурсивно обойти правое поддерево Т.
В простейшем случае функция f может выводить значение пары (K, V). При использовании операции INFIX_TRAVERSE будут выведены все пары в порядке возрастания ключей. Если же использовать PREFIX_TRAVERSE, то пары будут выведены в порядке, соответствующем описанию дерева, приведённого в начале статьи.
Разбиение дерева по ключу
правитьОперация «разбиение дерева по ключу» позволяет разбить одно дерево поиска на два: с ключами <K0 и ≥K0.
Этот раздел не завершён. |
Объединение двух деревьев в одно
правитьОбратная операция: есть два дерева поиска, у одного ключи <K0, у другого ≥K0. Объединить их в одно дерево.
У нас есть два дерева: T1 (меньшее) и T2 (большее). Сначала нужно решить, откуда взять корень: из T1 или T2. Стандартного метода нет, возможные варианты:
- Взять наугад (см. декартово дерево).
- Если в каждом узле дерева поддерживается размер всей ветви (см. дерево с неявным ключом), легко можно оценить дисбаланс для того и другого варианта.
алг ОбъединениеДеревьев(T1, T2) если T1 пустое, вернуть T2 если T2 пустое, вернуть T1 если решили сделать корнем T1, то T = ОбъединениеДеревьев(T1.правое, T2) T1.правое = T вернуть T1 иначе T = ОбъединениеДеревьев(T1, T2.левое) T2.левое = T вернуть T2
Балансировка дерева
правитьВсегда желательно, чтобы все пути в дереве от корня до листьев имели примерно одинаковую длину, то есть чтобы глубина и левого, и правого поддеревьев была примерно одинакова в любом узле. В противном случае теряется производительность.
В вырожденном случае может оказаться, что всё левое дерево пусто на каждом уровне, есть только правые деревья, и в таком случае дерево вырождается в список (идущий вправо). Поиск (а значит, и удаление и добавление) в таком дереве по скорости равен поиску в списке и намного медленнее поиска в сбалансированном дереве.
Для балансировки дерева применяется операция «поворот дерева». Поворот налево выглядит так:
- было Left(A) = L, Right(A) = B, Left(B) = C, Right(B) = R
- поворот меняет местами A и B, получая Left(A) = L, Right(A) = C, Left(B) = A, Right(B) = R
- также в узле Parent(A) меняется ссылка, ранее указывавшая на A, после поворота она указывает на B.
Поворот направо выглядит так же, достаточно заменить в вышеприведенном примере все Left на Right и обратно. Достаточно очевидно, что поворот не нарушает упорядоченность дерева и оказывает предсказуемое (+1 или −1) влияние на глубины всех затронутых поддеревьев. Для принятия решения о том, какие именно повороты нужно совершать после добавления или удаления, используются такие алгоритмы, как «красно-чёрное дерево» и АВЛ. Оба они требуют дополнительной информации в узлах — 1 бит у красно-чёрного или знаковое число у АВЛ. Красно-чёрное дерево требует не более двух поворотов после добавления и не более трёх после удаления, но при этом худший дисбаланс может оказаться до 2 раз (самый длинный путь в 2 раза длиннее самого короткого). АВЛ-дерево требует не более двух поворотов после добавления и до глубины дерева после удаления, но при этом идеально сбалансировано (дисбаланс не более, чем на 1).
См. также
правитьСбалансированные деревья:
Примечания
править- ↑ Роман Акопов. Двоичные деревья поиска. RSDN Magazine #5-2003 (13 марта 2005). Дата обращения: 1 ноября 2014. Архивировано 1 ноября 2014 года.
Для улучшения этой статьи желательно:
|