Граф дуг окружности
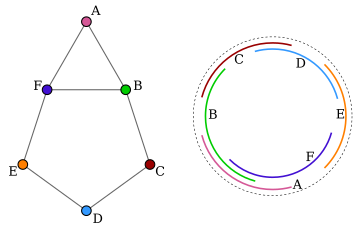
В теории графов графом дуг окружности называется граф пересечений множества дуг окружности. Граф имеет одну вершину для каждой дуги окружности и ребро между двумя вершинами, если соответствующие дуги пересекаются.
Формально, пусть
— множество дуг. Тогда соответствующий им граф дуг окружности — это G = (V, E), где
и
Семейство дуг, соответствующее графу G, называется дуговой моделью.
Распознавание
правитьТукер [1] нашёл первый полиномиальный алгоритм распознавания для графов дуг окружности, работающий за время . Позднее МакКоннел [2] нашёл первый линейный алгоритм распознавания за время .
Связь с другими классами графов
правитьГрафы дуг окружности являются естественным обобщением интервальных графов. Если граф дуг окружности G имеет дуговую модель, не покрывающую некоторые точки окружности, окружность можно разорвать в такой точке и выпрямить в отрезок, что даёт интервальное представление. Однако, в отличие от интервальных графов, графы дуг окружности не всегда совершенны, поскольку нечётные циклы без хорд C5, C7, и т. д. являются графами дуг окружности.
Некоторые подклассы
правитьНиже пусть — произвольный граф.
Графы единичных дуг окружности
правитьявляется графом единичных дуг окружности, если существует дуговая модель, в которой все дуги имеют одинаковую длину.
Правильные графы дуг окружности
правитьявляется правильным графом дуг окружности (или цикловым интервальным графом[3]), если существует соответствующая дуговая модель, в которой никакая дуга не содержит полностью другую. Распознавание таких графов и построение правильной дуговой модели можно осуществить за линейное время .[4]
Циркулярные графы дуг Хелли
правитьявляется циркулярным графом дуг Хелли, если существует соответствующая дуговая модель такая, что дуги образуют семейство Хелли. Гаврил[5] даёт описание этого класса, из которого вытекает алгоритм распознавания за время .
Йорис и соавторы[6] дают другие характеристики (включая перечисление запрещённых порождённых подграфов) этого класса, откуда вытекает алгоритм распознавания, работающий за время O(n+m). Если входной граф не является циркулярным графом дуг Хелли, то алгоритм возвращает подтверждение этого факта в виде запрещённого порождённого подграфа. Они дали также алгоритм определения, образует ли данная циркулярная дуговая модель семейство Хелли, за время O(n).
Приложения
правитьЦиркулярные графы дуг полезны при моделировании задач периодического распределения ресурсов[англ.] в исследовании операций. Каждый интервал представляет запрос на определённый период, повторяющийся во времени.
Примечания
правитьСсылки
править- Benson L. Joeris, Min Chih Lin, Ross M. McConnell, Jeremy P. Spinrad, Jayme L. Szwarcfiter. Linear-Time Recognition of Helly Circular-Arc Models and Graphs // Algorithmica. — 2009. — Т. 59, вып. 2. — С. 215–239. — doi:10.1007/s00453-009-9304-5..
- Alan Tucker. An efficient test for circular-arc graphs // SIAM Journal on Computing. — 1980. — Т. 9, вып. 1. — С. 1–24. — doi:10.1137/0209001..
- Ross McConnell. Linear-time recognition of circular-arc graphs // Algorithmica. — 2003. — Т. 37, вып. 2. — С. 93–147. — doi:10.1007/s00453-003-1032-7.
- Martin Charles Golumbic. Algorithmic Graph Theory and Perfect Graphs. — Academic Press, 1980. — ISBN 0-444-51530-5. Second edition, Annals of Discrete Mathematics 57, Elsevier, 2004.
- Xiaotie Deng, Pavol Hell, Jing Huang. Linear-Time representation algorithms for proper circular-arc graphs and proper interval graphs // SIAM Journal on Computing. — 1996. — Т. 25, вып. 2. — С. 390–403. — doi:10.1137/S0097539792269095..
- Fanica Gavril. Algorithms on circular-arc graphs // Networks. — 1974. — Т. 4, вып. 4. — С. 357–369. — doi:10.1002/net.3230040407.
- circular arc graph. Information System on Graph Class Inclusions. Дата обращения: 14 декабря 2013. Архивировано 21 декабря 2013 года.
- Maria Chudnovsky, Paul Seymour. Claw-free graphs. III. Circular interval graphs // Journal of Combinatorial Theory. — 2008. — Т. 98, вып. 4. — С. 812–834. — doi:10.1016/j.jctb.2008.03.001..
Для улучшения этой статьи желательно:
|


